目标检测系列(6)—YOLOv4 让每个人都能体验深度学习给我们带来的快乐(中)

企业开发 2022-08-02 14:01
0 阅读

携手创作，共同成长！这是我参与「掘金日新计划 · 8 月更文挑战」的第7天，点击查看活动详情

前言

最近在看 YOLOv4 一些相关资料，不得不说 YOLOv4 是当时技术的万花筒。将神经网络当时各个阶段、数据预处理、网络结构和训练中出现技术都进行工程上尝试进行融合。

损失函数

简单回顾一下在一阶段目标检测模型中的一些常用的损失函数

MSE 损失函数
∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 + ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] \sum_{i=0}^{S^2}\sum_{j=0}^B \mathbb{1}^{obj}_{ij} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 + (w_i - \hat{w}_i)^2 + (h_i - \hat{h}_i)^2\right]
YOLO 损失函数
∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 + ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] \sum_{i=0}^{S^2}\sum_{j=0}^B \mathbb{1}^{obj}_{ij} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 + (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2\right]
SSD 损失函数
L L o c ( x , l , g ) = S m o o t h L 1 ( 1 2 ∑ i j x i j ∣ ∣ l i − g j ∣ ∣ 2 ) L_{Loc}(x,l,g) = Smooth_{L_1} (\frac{1}{2} \sum_{ij} x_{ij}||l_i - g_j||^2)

上面列出这几种损失函数中基本都属于 L2 损失函数，其中 YOLO 为了解决 scale 敏感对于宽高进行开方处理。

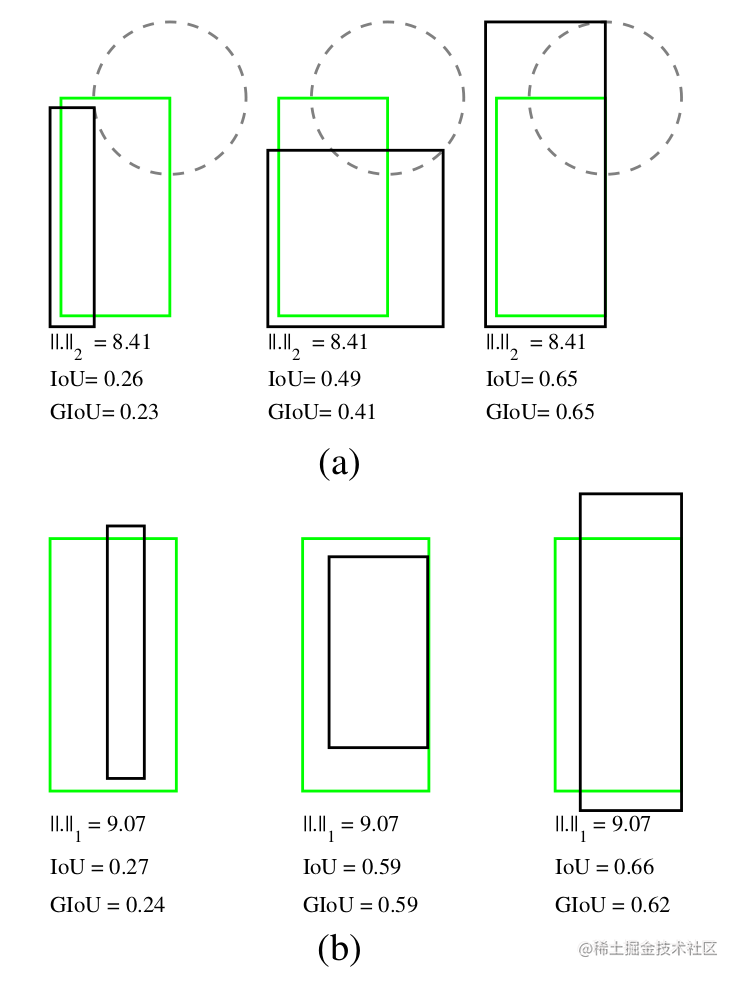
giou_001.png

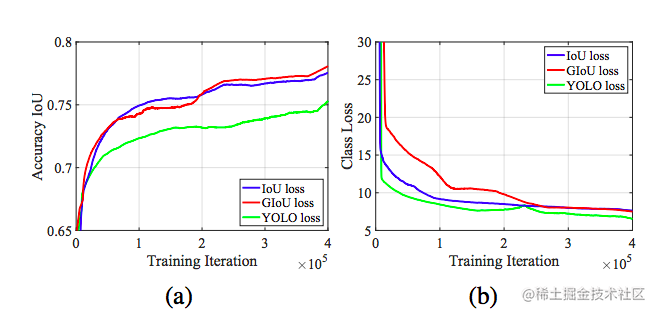
不过我们在做对目标检测的评估时常常用的都是 IoU 来衡量，我们来看 (a) 中，在这些框中，他们计算 L2 损失值都是 8.41 相对于

IoU 损失函数

在之前采用 MSE 来计算定位损失函数，在计算过程中，关于中心点、宽和高的损失都是单独考虑的，实际上中心点和宽高是存在一定关系的，所以采用 IoU 方式作为损失函数感觉更合理，而且在目标检测中评估都会采用 IoU 来进行评估

L I o U = 1 − I o U I o U = A ∩ B A ∪ B L_{IoU} = 1 - IoU\\ IoU = \frac{A \cap B}{A \cup B}
IoU 的性质
  • 具有尺度不变性，这是因为 IoU 是一个比值概念，所以对于尺度不敏感

下面来通过一个例子来介绍 IoU 尺度不变性

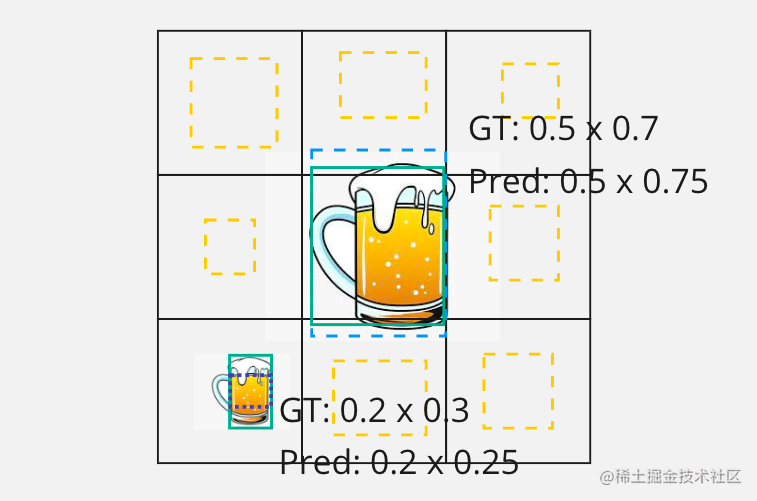
yolov4_051.png

我们来看上面图中出现两个大小不同目标，之前在介绍 YOLOv1 可能大家已经看过这张图，在图中我们分别给出了目标边界框尺寸和预测边界框的尺寸，接下来就是通过 L2 方式来分别计算大目标和小目标的宽高的损失

( ( 0.5 − 0.5 ) 2 + ( 0.75 − 0.7 ) 2 ) = ( 0.05 ) 2 ( ( 0.5 − 0.5 ) 2 + ( 0.25 − 0.3 ) 2 ) = ( 0.05 ) 2 ((0.5 - 0.5)^2 + (0.75 - 0.7)^2) = (0.05)^2\\ ((0.5 - 0.5)^2 + (0.25 - 0.3)^2) = (0.05)^2

他们计算宽高损失值是相同，这显然是有问题的，对于大目标 0.05 偏差并不明显，而对于小目标来说同样大小偏差影响却很大。所以在 YOLOv1 在计算宽高损失时因为开方的计算。

那么我们再来看一看通过 IoU 来计算的效果

I o U l a r g e = 0.5 × 0.7 0.5 × 0.75 = 0.93 IoU_{large} = \frac{0.5 \times 0.7}{0.5 \times 0.75} = 0.93
I o U s m a l l = 0.25 × 0.2 0.3 × 0.2 = 0.83 IoU_{small} = \frac{0.25 \times 0.2}{0.3 \times 0.2} = 0.83

从上面计算结果来看，通过 IoU 计算结果反应通常面积差异值对于不同大小目标损失值贡献是不同的

L I o U = 1 − I o U L_{IoU} = 1 - IoU

那么就根据 IoU

L I o U l a r g e = 1 − 0.93 = 0.07 L_{IoU_{large}} = 1 - 0.93 = 0.07
L I o U s m a l l = 1 − 0.83 = 0.17 L_{IoU_{small}} = 1 - 0.83 = 0.17

那么 IoU 损失函数又存在什么样限制呢?我们来看一个例子，对于两个两个没有覆盖边界框 A he B 如上图，同样是没有覆盖两个边界框 A 和 B，在左侧要优于右侧，不过他们的 IoU 值是相同的。我们是需要在损失函数上将这两种不同情况反应出来，所以就引入 GIoU

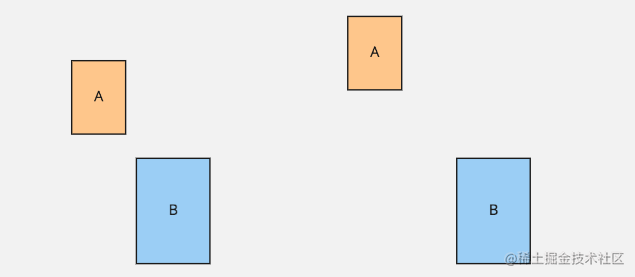
yolov4_033.png

这里因为 A 和 B 没有重合，所以 IoU 为 0 所以在这个阶段模型是学习不到东西

GIoU 损失函数

L G I o U = 1 − I o U + ∣ C − A ∪ B ∣ ∣ C ∣ L_{GIoU} = 1 - IoU + \frac{|C - A\cup B|}{|C|}
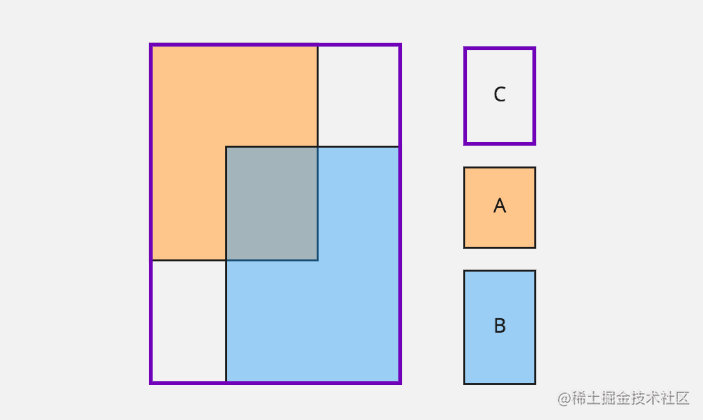
yolov4_017.png
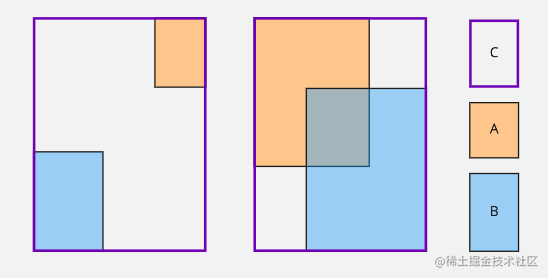
  • A 和 B 分别表示边界框
  • C 表示将 A 和 B 包裹的边界框

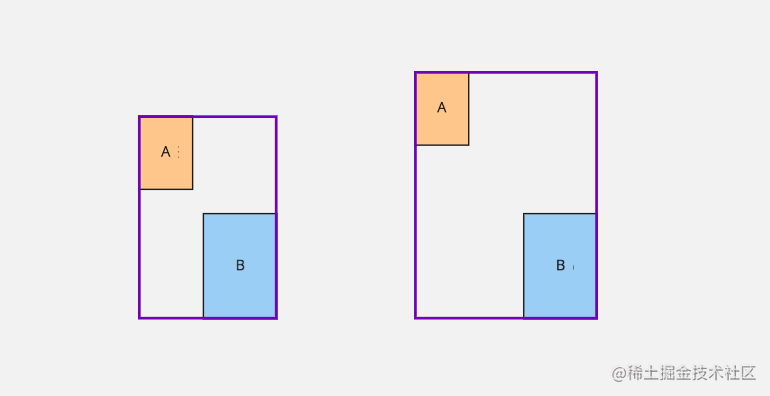
yolov4_032.png

G I o U = − 100 − ( 20 + 30 ) 100 = − 0.5 GIoU = - \frac{100 - (20 + 30)}{100} = -0.5
G I o U = − 200 − ( 20 + 30 ) 200 = − 0.75 GIoU = - \frac{200 - (20 + 30)}{200} = -0.75

所以 GIoU 值是介于 -1 到 1 之间的值，从上面 GIoU 计算结果来看

L G I o U = 1 − G I o U L_{GIoU} = 1 - GIoU

所以上面分别计算损失值为 1 − ( − 0.5 ) = 1.5 1 - (-0.5) = 1.5 而另一个为 1 − ( − 0.75 ) = 1.75 1 - (-0.75) = 1.75 现在从结果上来看 loss 是可以反映出

  • GIoU 对 scale 不敏感
  • GIoU 可以看做是 IoU 的下限，当两个边界框完全重合 GIoU = IoU
giou = iou - _true_divide(area_covering - area_union, area_covering)

yolov4_031.png

yolov4_035.png

GIoU 退化问题

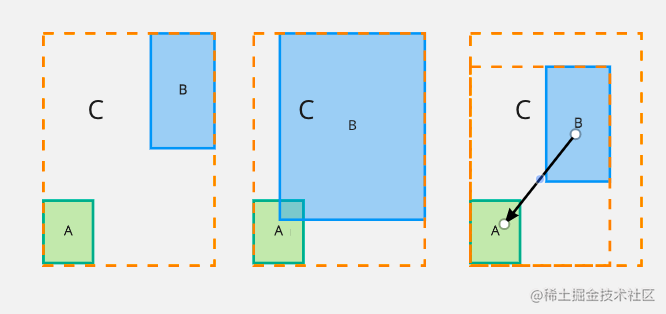
看下面的图，当其中一个边界框完全包裹了另一个边界框，GIoU 也就退化为 IoU 损失，例如下面 3 种情况中，对于这 3 种情况 GIoU 给出分数是完全相同的，然后显然第 3 种情况要优于前 2 种情况，因为两个边界框中心点位置重合，所以我们希望设计出损失函数是可以区分以下情况的不同的。

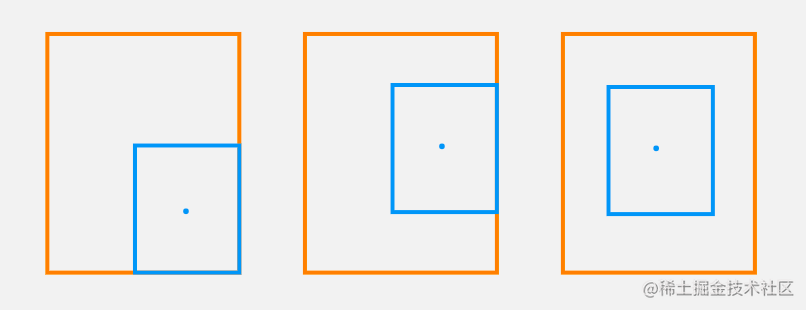
yolov4_022.png

所以我们需要增加两个边界框中心点间距离惩罚项，这样一来就使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。

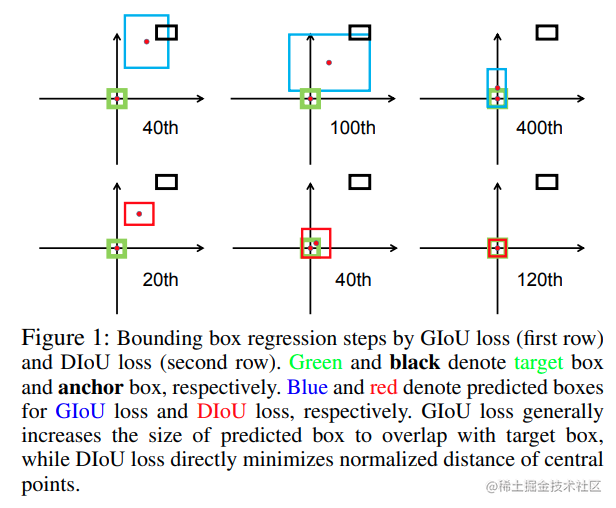
GIoU_005.png

我们再来看这张图，这张图解释了 GIoU 在训练过程收敛慢的原因。其中绿色为目标编辑框，黑色边界框表示锚框，蓝色表示模型给出预测边界框，预测边界框从锚框出发，不断取拟合目标边界框。

yolov4_028.png

L G I o U = 1 − I o U + ∣ C − A ∪ B ∣ ∣ C ∣ L_{GIoU} = 1 - IoU + \frac{|C - A \cup B|}{|C|}

从上面 GIoU 损失函数公式来看，这里 IoU = 0 而且 C 假设是固定大小，那么想要最小化 L G I o U L_{GIoU} 损失函数，就需要增加 B 的面积来减少 GIoU 损失函数，这样一来就会出现下图中一行情况，蓝色预测框会先不断扩大直到与绿色的目标边界框重合后再逐渐减少来拟合。

GIoU_005.png

那么也就是说明在 GIoU 中正则项是存在问题，需要将其替换掉

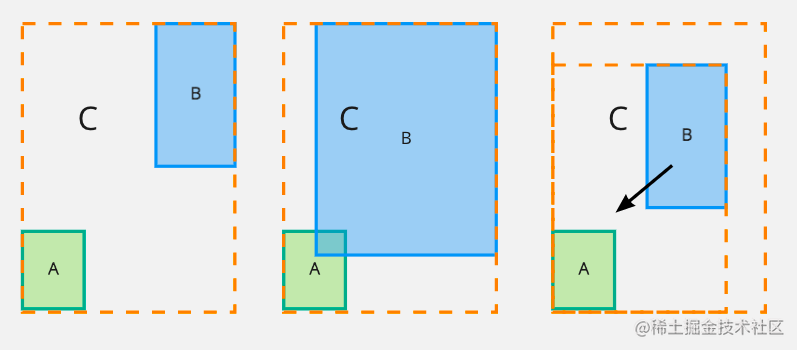
yolov4_027.png

我们希望 B 是通过移动逐渐接近 A 来减少损失，而不是先是扩大面积，然后再减少面积这种方式来实现拟合

DIoU

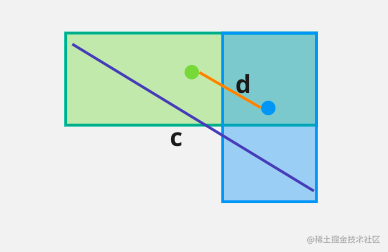
考虑两个边界框中心点距离

L D I o U = 1 − I o U + d 2 c 2 L_{DIoU} = 1 - IoU + \frac{d^2}{c^2}

yolov4_036.png

CIoU

一个好的损失函数需要涵盖以下几点

  • 覆盖率
  • 中心点距离
  • 以及宽高比

所以设计出 CIoU 损失来满足以上这些需求

L C I o u = 1 − I o U + d 2 c 2 + α v L_{CIou} = 1 - IoU + \frac{d^2}{c^2} + \alpha v

这里 v 用来计算宽高的相似性

v = 4 π 2 ( arctan ⁡ w g t h g t − arctan ⁡ w h ) 2 v = \frac{4}{\pi^2} \left( \arctan \frac{w^{gt}}{h^{gt}} - \arctan \frac{w}{h} \right)^2
α = v ( 1 − I o U ) + v \alpha = \frac{v}{(1 - IoU) + v}

这里 α \alpha 作用是当两个边界框距离比较远时候，就不会先取调整宽高，也就是忽略宽高的正则项。因为 IoU 是 0 到 1 之间数据，当为 0 时候 α v \alpha v 就是一个比较小数

数据增强

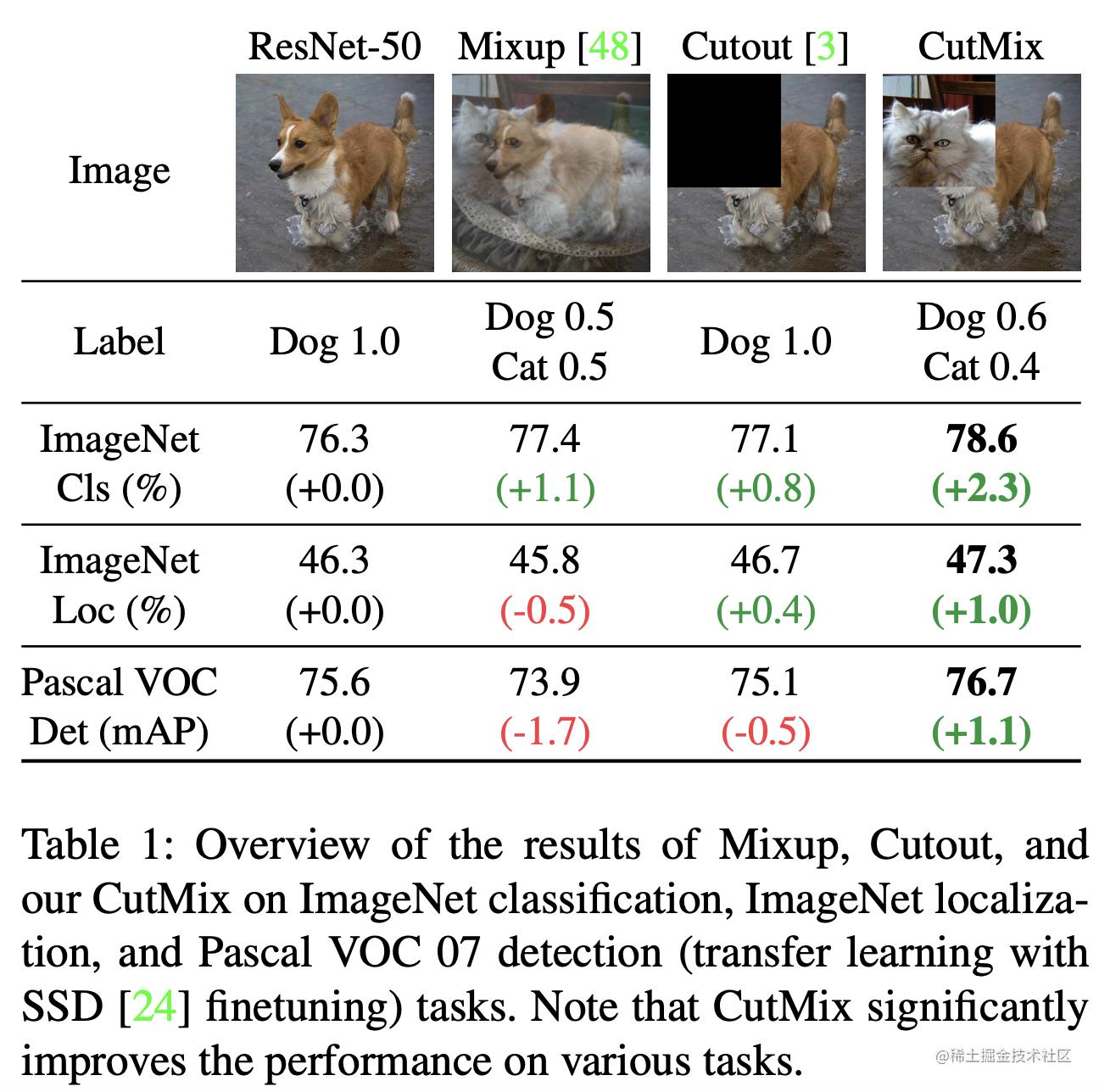
data_augmentation_001.png

  • Mixup: 这个很好理解就是将两张图像乘以一定权重然后进行混合
  • Cutout: 将图像一部分内容去除
  • CutMix: 将另一张图像提取一小块图像后和当前图像进行合成

Mosaic 数据增强

  • 首先增加图像样本的多样性
  • 由于每张图像相当于 4 张图像，从侧面增加了每一个 batch 图像的数量
  • 因为每次都会用到 batch normalization，所以希望每次样本数越多，那么批量的 BN 就越接近于整个样本的 BN

参考文章

  • Mish: A Self Regularized Non-Monotonic Neural Activation Function
  • Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

猜你喜欢

目录

热门文章