目录
此示例说明如何以新的均匀速率对非均匀采样的信号进行重采样。它说明如何对不规则采样数据应用自定义滤波器以减少混叠。它还说明如何使用去趋势来去除信号开始和结束位置的瞬变。
以所需采样率对非均匀采样信号进行重采样
resample 函数允许将非均匀采样信号转换为使用新的均匀采样率。
创建一个以大约 48 kHz 采样率不规则采样的 500 Hz 正弦波。我们通过向均匀向量添加随机值来模拟不规则性。
rng default
nominalFs = 48000;
f = 500;
Tx = 0:1/nominalFs:0.01;
irregTx = sort(Tx + 1e-4*rand(size(Tx)));
x = sin(2*pi*f*irregTx);
plot(irregTx,x,'.')如图所示:
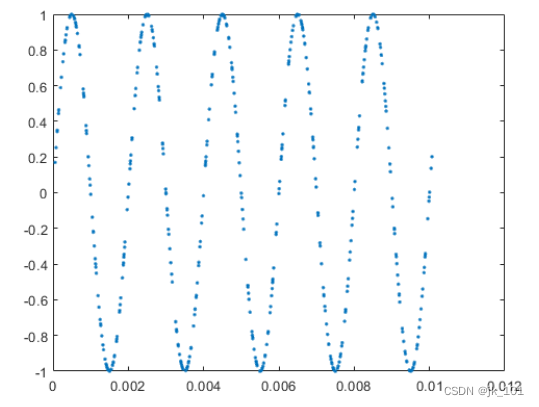
要对非均匀采样信号进行重采样,可以调用带时间向量输入的 resample。下一个示例将我们的原始信号转换为均匀的 44.1 kHz 采样率。
desiredFs = 44100;
[y, Ty] = resample(x,irregTx,desiredFs);
plot(irregTx,x,'.-',Ty,y,'o-')
legend('Original','Resampled')
ylim([-1.2 1.2])如图所示:
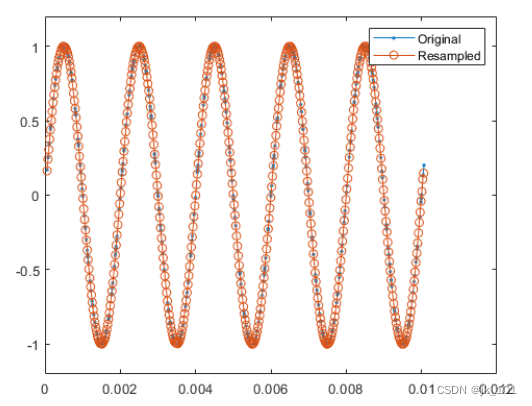
可以看到,经过重采样的信号与原始信号具有相同的形状和大小。
选择插值方法
resample 中的转换算法在输入采样尽可能接近等间距时效果最佳,因此观察采样数据中缺失一部分输入采样时可能发生的情况很有意义。
下一个示例使输入正弦波的第二个波峰出现陷波,并对其应用重采样。
irregTx(105:130) = [];
x = sin(2*pi*f*irregTx);
[y, Ty] = resample(x,irregTx,desiredFs);
plot(irregTx,x,'. ')
hold on
plot(Ty,y,'.-')
hold off
legend('Original','Resampled')
ylim([-1.2 1.2])如图所示:
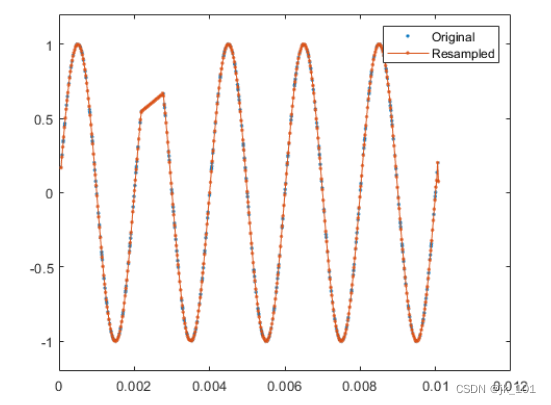
缺失段通过线性插值进行连接。线性插值是 resample 函数对非均匀采样数据进行重采样所使用的默认方法。
在某些情况下,如果您的输入中有缺失数据或较大空缺,可以通过选择不同插值方法来还原一些缺失数据。
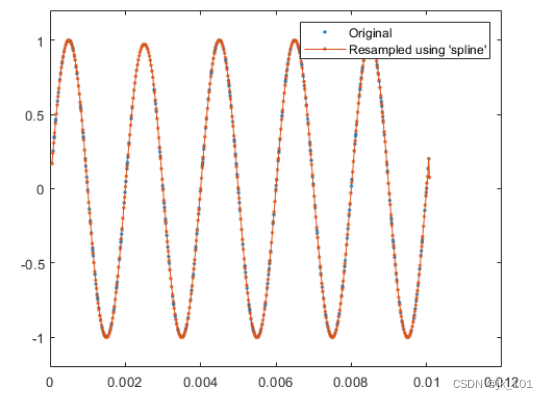
对于低噪声、低带宽信号,样条插值在重新构造原始信号时非常有效。要在重采样过程中使用三次样条,请提供 'spline' 插值方法:
[y, Ty] = resample(x,irregTx,desiredFs,'spline');
plot(irregTx,x,'. ')
hold on
plot(Ty,y,'.-')
hold off
legend('Original','Resampled using ''spline''')
ylim([-1.2 1.2])如图所示:
控制插值网格
默认情况下,resample 会构造一个中间网格,该网格是信号的所需采样率与平均采样率之比的有理逼近值。
如果输入采样的一部分包含高频分量,可以通过选择整数系数 p 和 q 来选择此有理比率,从而控制中间网格的间距。
检查欠阻尼二阶滤波器的阶跃响应,该滤波器以约 3 Hz 的频率振荡:
w = 2*pi*3;
d = .1002;
z = sin(d);
a = cos(d);
t = [0:0.05:2 3:8];
x = 1 - exp(-z*w*t).*cos(w*a*t-d)/a;
plot(t,x,'.-')
如图所示:
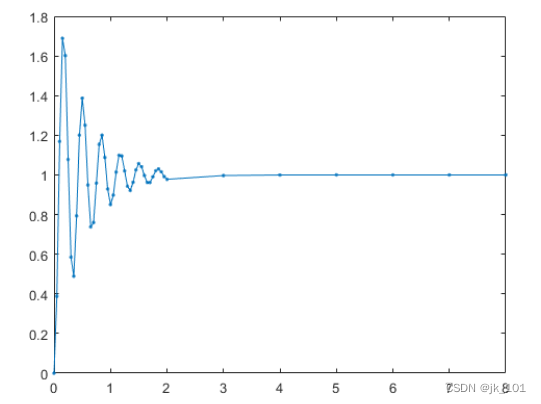
阶跃响应在振荡时以高速率采样,在不振荡时以低速率采样。现在仅使用默认设置以 100 Hz 对信号进行重采样:
Fs = 100;
[y, Ty] = resample(x,t,Fs);
plot(t,x,'. ')
hold on
plot(Ty,y)
hold off
legend('Original','Resampled (default settings)')如图所示:
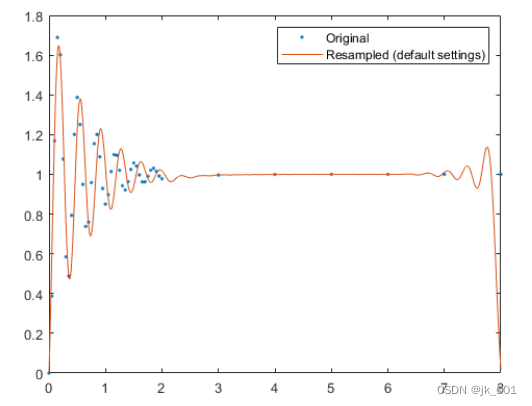
波形开始时的振荡包络衰减,并且比原始信号振荡得更慢。默认情况下,resample插值到与输入信号的平均采样率对应的等间距网格中。
avgFs = (numel(t)-1) /(t(end)-t(1))
avgFs = 5.7500该网格的采样率应高于您要测量的最大频率的两倍。该网格的采样率为每秒 5.75 个采样,低于振铃频率的奈奎斯特采样率 6 Hz。
为了使网格具有更高的采样率,可以提供整数参数 p 和 q。resample 将网格的采样率调整为 Q*Fs/P,对信号进行插值,然后应用其内部采样率转换器(按 P 进行上采样,按 Q 进行下采样)来还原所需的采样率 Fs。使用 rat 选择 p 和 q。
由于振荡的振铃频率为 3 Hz,请指定采样率为 7 Hz 的网格,该采样率略高于奈奎斯特速率。1 Hz 的余量是考虑到指数包络衰减产生的额外频率成分。
Fgrid = 7;
[p,q] = rat(Fs/Fgrid)
p = 100
q = 7
%%
[y, Ty] = resample(x,t,Fs,p,q);
plot(t,x,'.')
hold on
plot(Ty,y)
hold off
legend('Original','Resampled (custom P and Q)')如图所示:

指定抗混叠滤波器
在下一个示例中,可以查看测量飞机发动机节气门设置的数字化仪的输出。节气门设置以约 100 Hz 的名义速率进行非均匀采样。我们将尝试以均匀的 10 Hz 速率对此信号进行重采样。
以下是我们的原始信号的采样。
load engineRPM
plot(t,x,'.')
xlabel('Time (s)')
ylabel('RPM')如图所示:
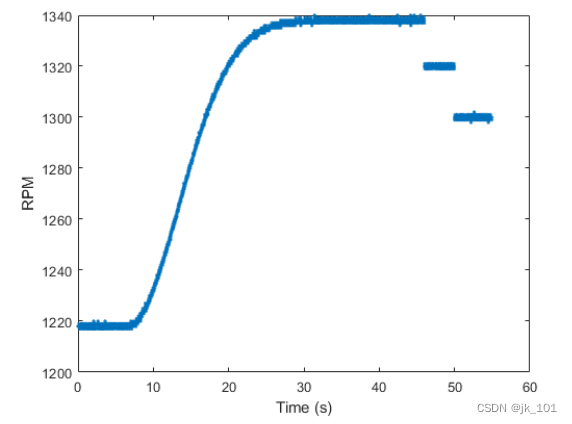
我们的信号经过量化。现在放大时间间隔从 20 秒到 23 秒的上升区域:
plot(t,x,'.')
xlim([20 23])如图所示:
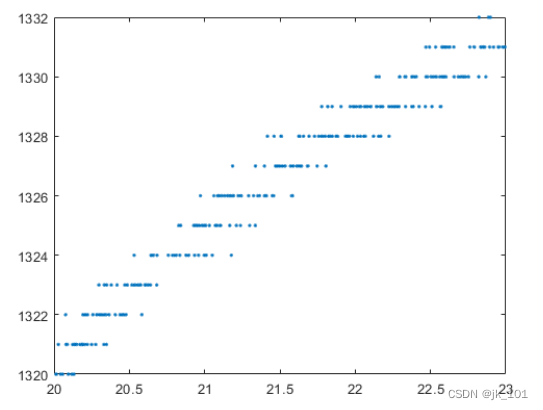
信号在此区域内缓慢变化。这允许您通过在重采样器中使用抗混叠滤波器来去除一些量化噪声。
desiredFs = 10;
[y,ty] = resample(x,t,desiredFs);
plot(t,x,'.')
hold on
plot(ty,y,'.-')
hold off
xlabel('Time')
ylabel('RPM')
legend('Original','Resampled')
xlim([20 23])如图所示:
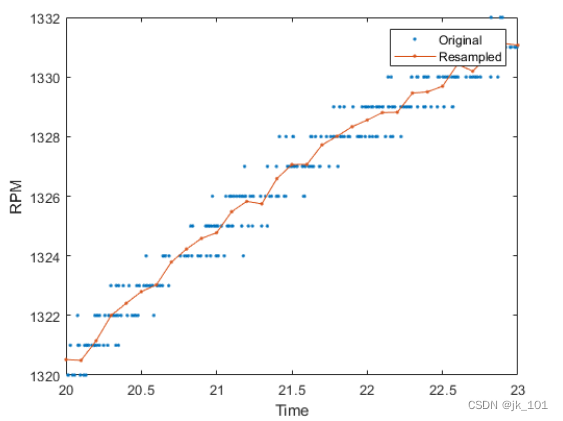
这相当有效。然而,通过为 resample 提供具有低截止频率的滤波器,可以进一步对重采样的信号进行平滑处理。
首先,将网格间距设置为大约我们的名义 100 Hz 采样率。
nominalFs = 100;接下来,确定合理的 p 和 q 以获得所需的速率。由于名义速率为 100 Hz,而我们所需的速率为 10 Hz,因此需要按 10 进行抽取。这等效于将 p 设置为 1,将 q 设置为 10。
p = 1;
q = 10;可以为 resample 提供自己的滤波器。为了获得适当的时序对齐,滤波器应为奇数长度。滤波器长度应比 p 或 q 大几倍(以较大者为准)。将截止频率设置为所需截止频率的 1/q,然后将生成的系数乘以 p。
% ensure an odd length filter
n = 10*q+1;
% use .25 of Nyquist range of desired sample rate
cutoffRatio = .25;
% construct lowpass filter
lpFilt = p * fir1(n, cutoffRatio * 1/q);
% resample and plot the response
[y,ty] = resample(x,t,desiredFs,p,q,lpFilt);
plot(t,x,'.')
hold on
plot(ty,y)
hold off
xlabel('time')
ylabel('RPM')
legend('Original','Resampled (custom filter)','Location','best')
xlim([20 23])
如图所示:
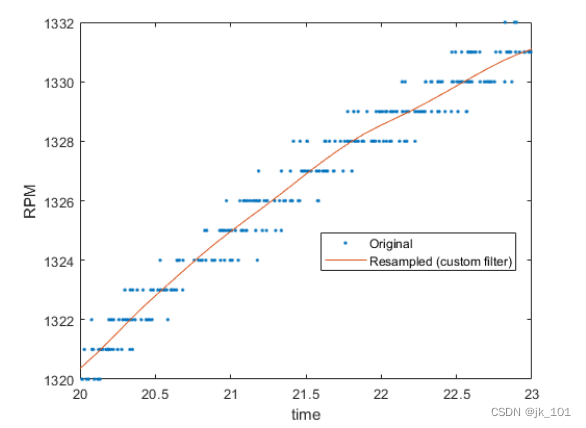
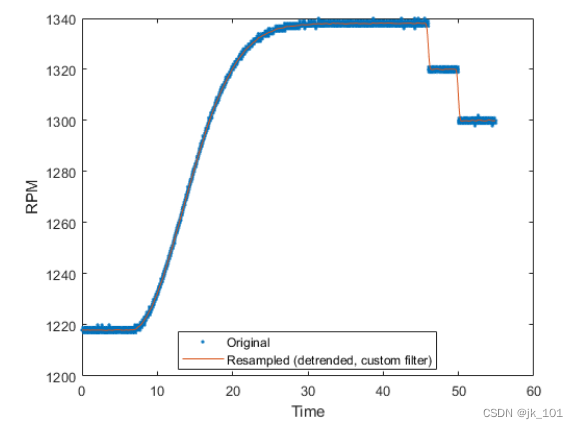
去除端点效应
现在缩小以查看我们的原始信号。请注意,端点处有明显的偏移。
plot(t,x,'.',ty,y)
xlabel('time')
ylabel('RPM')
legend('original','resampled (custom filter)','Location','best')如图所示:
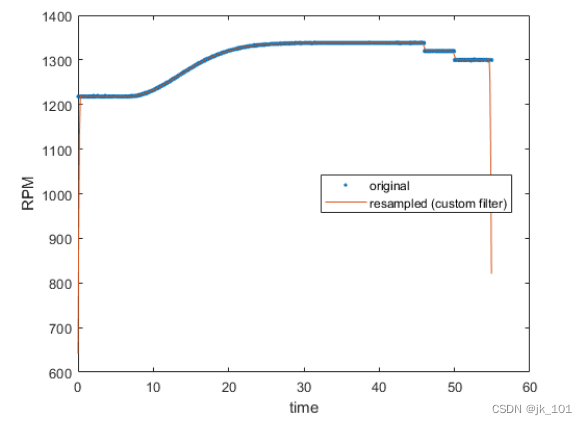
出现这些伪影是因为 resample 假设信号边界之外的信号为零。为了减少这些不连续性的影响,请减去信号端点之间的一条线,执行重采样,然后将该线添加回原始函数。要实现这一点,可以计算第一个和最后一个采样之间直线的斜率和偏移量,并使用 polyval 构造要减去的线。
% compute slope and offset (y = a1 x + a2)
a(1) = (x(end)-x(1)) / (t(end)-t(1));
a(2) = x(1);
% detrend the signal
xdetrend = x - polyval(a,t);
plot(t,xdetrend)如图所示:
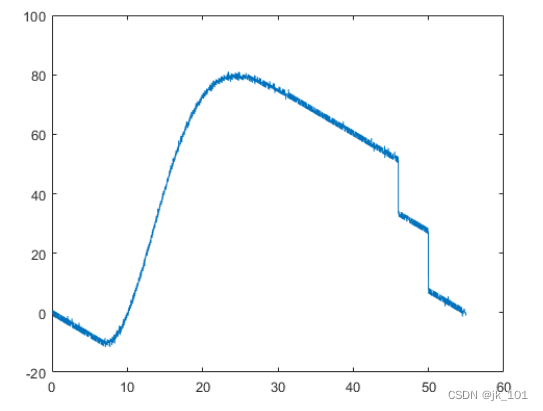
现在,去趋势后的信号的两个端点都接近于零,这减少了引入的瞬变。调用 resample,然后添加回趋势。
[ydetrend,ty] = resample(xdetrend,t,desiredFs,p,q,lpFilt);
y = ydetrend + polyval(a,ty);
plot(t,x,'.',ty,y)
xlabel('Time')
ylabel('RPM')
legend('Original','Resampled (detrended, custom filter)','Location','best')如图所示:
总结
此示例说明如何使用 resample 将均匀和非均匀采样信号转换为固定速率。