智力题在目前的大厂面试中也是非常常见的,这种题的特点是看过一遍就基本能答上来,没看过可能就比较费劲,所以性价比比较高。之前总结过一些,大家有兴趣可以看看。
1.一副牌除去大小王还有52张,其中10张牌是正面朝上的,要求一个盲人将牌分成两堆,并且每堆牌正面朝上的数量相同,可以任意翻动每张牌,应该怎么分
这个问题不算复杂,看过一遍就能记住答案。分成两堆,一堆10张,一堆42张,并且将第一堆的10张牌全部反转,这时两堆牌中正面朝上的数量是相同的。
2.两人玩游戏,在脑门上贴数字(正整数>=1),只看见对方的,看不见自己的,而且两人的数字相差1,以下是两人的对话:A:我不知道,B:我也不知道,A:我知道了,B:我也知道了,问A头上的字是多少,B头上的字是多少?
这个问题关键是数字是大于等于1的数字,只有对方脑门上贴的是1,才能一次猜出自己的数字,所以1这个数字很关键,不是在对方脑门上,就是自己脑门上的两个可能数字之一,这个条件是必须要用上的。
第一轮:A说不知道,B也说不知道,说明两个人脑门上都没有数字1。每个人脑门上的数字都有两种可能。
第二轮:A说知道了,B也说知道了,说明B说不知道给A排除了一个可能,只有数字1才有可能被排除,A才有可能猜出自己脑门上的数字,所以A脑门的数字是3。B听到A说知道了,说明自己说不知道给A排除了一个答案,排除的答案只能是1,A才能猜出,既然排除的是1,A只能是3,那么B脑门的数字则只能是2。
3.在一个飞机场有N架飞机,每架飞机只有一个油箱,每箱油可以使飞机绕地球飞半圈。如果使一架飞机绕地球一圈,至少需要出动多少飞机?(要求所有飞机均能安全返回到机场,只能通过飞机给飞机这样加油方式,不能降落到机场加油)
这个问题的思路是先将路程分为前半程和后半程,这样需要出动飞机会少些
具体细节可以看这个图
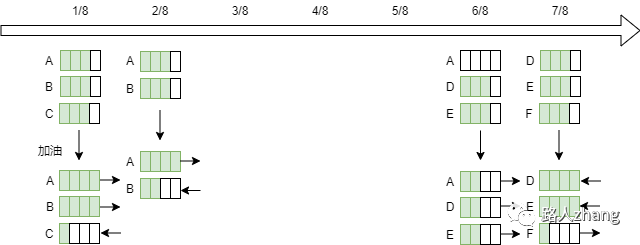
前半程:假设整个路程为1,A、B、C三架飞机同时起飞,在1/8处,三架飞机的油量都剩了3/4,其中飞机C给另外飞机A、B加满油,自己还剩1/4,刚好够返航到机场。到2/8处,A、B两架飞机的油量都剩了3/4,其飞机B给飞机A加满油后,自己还剩2/4,刚好能够返航。此时飞机A飞到6/8处时,油量为0。
后半程:D、E、F三架飞机同时反方向起飞,在7/8处,三架飞机的油量还剩了3/4,飞机F给飞机D、E加满后返航,D、E两架飞机在6/8处碰到飞机A,此时飞机A油量为0,D、E两架飞机的油量为3/4,分别给飞机A加1/4的油量。这时A、D、E飞机油量都是2/4,刚好够返航。
总结一下,几个加油的节点,分别在1/8,2/8,7/8,6/8处。
4.晚上有四个人需要过桥,但是只有一个手电筒,并且桥一次最多两个人,每个人通过桥所需的时间也不同,A、B、C、D过桥所需的时间分别为1、2、5、10分钟。请问如何过桥所需时间最短?
这个问题最开始想到的可能是让速度最快的人分别送其他三个人过去,因为他回来所需的时间最短。其实不是这样的,最佳的解决方案是将两个耗时最多的人一起过桥,而不是分开过桥,并且不需要返回。
第一次过桥:A和B一起过,需要2分钟,A再回来,所需1分钟,一共所需3分钟
第二次过桥:C和D一起过桥,需要10分钟,B再回来,所需2分钟,一共需12分钟
第三次过桥:A和B一起过桥,所需2分钟
一共所需17分钟。
5.一个人8块钱买了一只鸡,9块钱卖了,10块钱又买回来了,11块钱又卖了,请问他挣了多少钱?
2块钱
6.一共有N颗石子,每次最多取M颗最少取1颗,A,B轮流取(A先),谁最后拿完石子谁就获胜,请问最后谁会获胜?
这种没有具体的数字就要分类讨论下了
假设M>=N,那么A一次就把石子拿完了,A胜
假设M<N,如果N可以被(M+1)整除时,A失败,如果N不可以被(M+1)整除时,A胜
具体分析:如果N可以被(M+1)整除时,无论A怎么拿,B都会保持拿完后石子的数量为(M+1)的倍数,到最后只能M+1个,A无论怎么拿,B都会在下一次把石子拿完。如果N不可以被(M+1)整除时,A可以保证自己拿完剩下的石子数量一定是(M+1)的倍数,同理,A胜。
7.海盗分金币问题:5个海盗抢到了100枚金币,他们的分配方案,先抽签决定自己的发言顺序。1号提出的方案,由5个人进行投票表决,如果半数人以上同意(不包括半数),就按他的方案分配,否则扔进海里喂鱼。如果1号被喂鱼,由2号发言,提出的方案由4个人进行投票表决,规则同上。如果2号被喂鱼,以此类推。1号海盗提出什么样的方法才能使得自己分到最多的金币
这个题的思路主要是逆推法
从最后面开始,如果前三个人都被喂鱼了,只剩4号和5号,那么无论4号说什么,5号都会反对,4号一定会被喂鱼,5号独吞100枚金币。所以3号无论说什么,4号只能同意。
3号知道这些,会提出“100,0,0”这种分配方案,4号海盗为了活命只能赞同,加上自己一票即可使得投票通过半数。
2号知道这些,会提出“98,0,1,1”的分配方案,以此拉拢4号和5号。
1号知道这些,他还需要两个人支持他,2号是不可能的,3号只需1枚金币,4号或者5号其中一人即可,所以1号的分配方案是“97,0,1,2,0”或者“97,0,1,0,2”
拓展:如果题目改成投票半数人同意即可,又会怎样分配呢?
8.高层扔鸡蛋问题:有一个100层的高楼,给你两个鸡蛋,需要测试出在哪层楼扔鸡蛋,鸡蛋不会碎。鸡蛋如果没有碎可以扔无数次。最少需要扔多少次?
这是一个非常经典的动态规划问题,手撕代码时也很常见
如果是只有1个鸡蛋,这个问题就很简单了,为保证一定找到这个楼层,只能从第一层开始试。
题目中是两个鸡蛋,正常就是会想到二分法之类,先在50层扔一个,没碎,捡回来在75层扔,碎了,第二个鸡蛋只能从第1层开始试了。第一个鸡蛋用来缩短范围,第二个鸡蛋用来遍历范围。
假设需要x次才能找到临界的楼层,也就是说第一个鸡蛋从第x层扔出(因为需要考虑最差情况,万一第一个鸡蛋碎了,为保证x次能找到,第一个鸡蛋需要从x层扔出。因为如果鸡蛋恰好在第x层碎了,在第x-1层没碎,第一个鸡蛋在x层以上的楼层扔的话,第二个鸡蛋需要遍历x次,一共需要x+1次)
如果第一个鸡蛋碎了,第二个鸡蛋遍历1至x-1层,则需要x次找到。
如果第一个鸡蛋没碎,则第一个鸡蛋的任务是需要继续缩小范围,还是为了保持这个x次能找到临界楼层的条件,现在只剩x-1次了,下一次只能在x+x-1层扔第一个鸡蛋,以此类推,x+(x-1)+(x-2)+......+1>=100,x=14
也就是说最少需要扔14次。
这个问题还有一些变种问题,比如2个鸡蛋,n层楼;k个鸡蛋,n层楼(力扣887题,大家感兴趣可以看看)
如果本文对你有帮助,别忘记给我个3连 ,点赞,转发,评论,
咱们下期见!答案获取方式:已赞 已评 已关~
学习更多知识与技巧,关注与私信博主(03)
