动态多目标优化--基于决策变量分类的动态多目标进化算法 笔记

阅读论文：A Dynamic Multiobjective Evolutionary Algorithm
Based on Decision Variable Classification
（Zhengping Liang , Tiancheng Wu, Xiaoliang Ma, Zexuan Zhu , Member, IEEE,and Shengxiang Yang , Senior Member, IEEE）
这是2020年发布在IEEE上的一篇文章，主要讲的是基于决策分类的进化算法来解决动态多目标优化问题（DMOPs），由于本人也是才接触多目标进化没多久，学术功底有限，如果有不正确的地方欢迎批评指正！

前言

首先提出两个问题
1、什么是动态多目标优化问题（DMOPs）?
具有多个互相冲突且随着时间变化的多目标优化问题
2、动态多目标优化问题和多目标优化问题之间有什么区别呢？
动态=Dynamic 优化问题是指其目标函数不仅与决策变量有关，而且还会随着时间(环境)动态变化。
定义多目标问题（MOP）

定义动态多目标问题（DMOP）

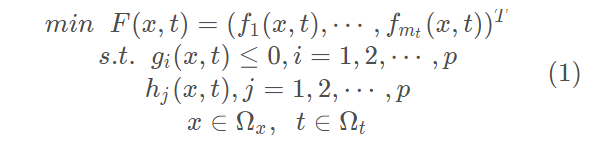
X = (x1,x2,…xn_t)代表n_t维的决策变量向量，主要是新增加了t：离散的时间实例，fm_t(x,t)表示x在时间t的第m_t个目标函数。n_t和m_t的值都会随时间变化。F(x,t)代表时间t评估解x的目标函数向量；p和q分别是不等式约束和等式约束的个数；g_i（x,t）代表第i个不等式约束；Ω_t代表可行的时间空间；

Abstract–摘要

现状：目前提出了许多动态多目标进化算法（DMOEAs）来解决DMOPs，主要是通过将多样性引入方法或预测方法与常规多目标进化算法相结合来解决。维持种群收敛性和分布性（Convergence and Diversity）的良好平衡对于DMOEAs的性能至关重要。

解决方案：提出了一种基于决策变量分类的DMOEA（DMOEA-DVC）。 DMOEA-DVC在静态进化和变化响应阶段分别将决策变量分为两个和三个不同的组。在静态进化中，两个决策变量组使用两种不同的交叉算子来加速收敛，同时保持良好的多样性。在变化响应中，DMOEA-DVC分别通过保持，预测和分布性引入策略来重新初始化三个决策变量组。

实验结果：在33个基准DMOPs上将DMOEA-DVC与其他六个典型的DMOEAs进行了比较。实验结果表明，DMOEA-DVC的总体性能优于或类似于所比较的算法。

Introduction–引言

• 从MOEAs 到 DMOEAs遇到的问题
  多目标进化算法（MOEAs）在各种静态多目标优化问题（MOPs）上都取得了成功。但是，由于在动态环境中缺少快速的变化响应机制，在DMOPs中它们往往会失败。
• 解决方法
  为了解决DMOPs，近年来已经提出了许多动态MOEAs（DMOEAs）。它们大部分可以被分为多样性引入方法（Diversity introduction approaches）和预测方法（prediction approaches）。

Diversity introduction approaches–多样性引入方法

多样性引入方法将一定比例的随机或突变个体引入进化种群以增加种群多样性。多样性的增加可以促进算法更好地适应新环境。但是，由于这些算法主要依靠静态进化搜索来找到引入多样性之后的最优解集，因此收敛速度可能会变慢。

prediction approaches–预测方法

预测方法采用预测模型来预测在变化的环境中有希望的种群。可以大大提高种群收敛性。然而，大多数预测模型需要一个训练周期，在训练周期中预测模型的性能不能令人满意。

主要问题

都没有考虑决策变量的不同特征。他们倾向于以相同的方式探索所有决策变量，这在平衡种群多样性和收敛性方面效率较低。

主要亮点（idea）

提出了基于决策变量分类（DMOEA-DVC）的DMOEA。分别在静态进化和变化响应阶段，使用两种决策变量分类方法将决策变量分为两个和三个不同的组。根据决策变量分类，将不同的进化算子和变化响应策略相应地应用于不同的组，以增强种群的分布性和收敛性。

1. 在静态进化和变化响应阶段分别使用两种不同的决策变量分类方法，使算法能够更有效地探索不同的决策空间。
2. 在静态进化中，引入了一种新的子代生成策略，该策略通过对两种不同类型的决策变量使用特定的交叉算子产生子代来加快种群收敛速度，同时保持算法的种群多样性。
3. 在变化响应中，提出了一种保持，预测和多样性引入相结合的混合响应策略来处理三种类型的决策变量，从而在不同的动态环境中实现更好的适应性。

Background–背景

A、DMOP基础

基于动态帕累托支配找到动态帕累托最优解或动态帕累托前沿面

1. 定义1（动态帕累托支配）：在时间t给出两个候选解x和y（x，y∈Ω），称x支配y，写为x（t）≺y（t），当且仅当
   
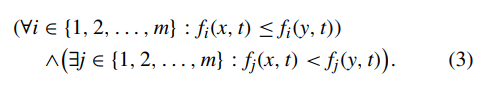
2. 定义2（动态帕累托最优解集）：在时间t的一个动态帕累托最优解集记为PS(t)，其中包括所有不被其他解支配的解，如下：
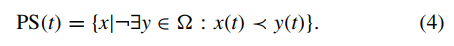
3. 定义3（动态帕累托前沿面）：在时间t的一个动态帕累托最优面记为PF(t)，是PS(t)中的解在目标函数空间中的映射，如下：
   
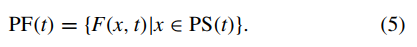
4. 定义4（多最优值变量）：给定一个决策变量i，若PS(t)中存在两个解x,y，并且xi≠yi，xi，yi分别指x，y在决策变量i上的值，则称i有多个最优值，是一个多最优值变量。
5. 定义5（单最优值变量）：给定一个决策变量i，对于PS(t)中任意两个解x,y，他们对应的决策变量i值是一样的，即xi=yi，则称i有单个最优值，是一个单最优值变量。

根据PF(t)和PS(t)的动态特性，将DMOP分为四种类型

扫描二维码关注公众号，回复： 14456886 查看本文章

• 类型I: PS(t)随时间变化，而PF(t)是固定的。
• 类型II: PS(t)和PF(t)都随时间变化。
• 类型三:PS(t)是固定的，PF(t)随时间变化。
• 类型IV: PS(t)和PF(t)都是固定的，但是随着时间的推移问题会改变。

B、动态多目标进化算法

1. 动态多目标算法（多样性引入）

通过看下面这个表格就非常直观，最终通过引入多样性方法可以防止种群陷入局部最优，并且易于实施。

2. 动态多目标算法之（基于预测的方法）

其中基于预测的方法中，也有很多在PPS算法的基础上，进行一些改进，最终也可以显示出提高收敛速度的能力。

C、决策变量分类方法

通过结合多样性引入和基于快速预测的方法来利用两者的优点，提出了一种增强的变化响应策略。

多样性引入或预测方法可以被视为搜索决策变量最优值的概率模型，大多数现有的DMOEAs都假定所有决策变量都处于相同的概率分布下。在实际的DMOPs中，决策变量的概率分布可能会发生很大变化。通过决策变量分类，可以将决策变量分为不同的组，然后可以将特定的概率搜索模型应用于相应的变量组以获得更好的解。

在静态中的决策变量分类

许多基于决策变量分类的MOEAs在静态MOPs上都取得了成功，决策变量扰动会产生大量个体用于分类，并成比例地消耗大量适应性评估。此策略对于静态MOPs效果很好，在静态MOPs中，决策变量的类别不变，并且仅需要分类一次。

在动态中的决策变量分类

• Woldesenbet和Yen [51]通过对目标空间变化的平均敏感度来区分决策变量，并以此为基础来重新安置个体。 该方法对于动态单目标优化问题效果很好，但是不适用于DMOP。
• Xu提出了一种针对DMOP的协作式协同进化算法，其中决策变量被分解为两个子组件，即相对于环境变量t不可分离和可分离的变量。应用两个种群分别协同优化两个子组件。文献中提出的算法在基于环境敏感性可分解决策变量的DMOP上具有优越性，但是，在许多DMOP中可能并非如此。

Framework–框架

具体过程：初始化父代种群P，然后从父代种群中选出一个子代种群P′和一个非支配解的档案A。在每次迭代中，在使用进化算子生成每个子代个体之前，对P使用决策变量分类方法，并将结果记录在布尔向量flag_multi中，其中每个元素指示相应的决策变量是多最优还是单最优变量。DMOEA-DVC可检测到进化过程中的任何潜在变化，如果检测到变化，则将使用变化响应策略，否则，将对个体的不同类型决策变量使用不同的交叉算子生成子代个体，生成子代个体后，更新P和A。在每一次迭代的末尾，从当前父代种群和子代种群的混合中选择一个新的子代种群和一个新的档案。

A、ClassificationSO–决策变量分类

在静态进化阶段(算法1第6行)使用决策变量分类，以增加生成高质量子代个体的可能性。
目标：找到在PF上分布均匀的种群，并尽快收敛到PF
方法：探索种群中非支配个体的邻居是很有效的
问题：如果子代的所有决策变量都是在非支配个体的决策变量附近生成的，则种群会陷入局部最优，为了避免这种情况，子代个体中的多最优值变量值应远离父代个体产生。

• 子代中的多最优变量值应该远离非支配个体产生，以保持良好的多样性。
• 对于单最优变量，子代个体中的生成值应尽可能接近父代个体中的相应值，以加速收敛。

关键问题：如何确定多最优值变量和单最优值变量

提出了一种区分多最优值变量和单最优值变量的近似方法。

在DMOP中，目标函数可能在某些决策变量上相互冲突。如果两个目标函数在决策变量上发生冲突，则该决策变量被视为具有多个最优值。（这个也很好理解，如果在X=C时存在两个最优的解，那么这两个目标相互冲突）

因此使用斯皮尔曼等级相关系数(SRCC)来衡量一个变量和一个目标函数之间的相关性。

如果第i个变量的两个目标函数之间存在明显的相关冲突（正相关与负相关），即max（ri1（t），ri2（t），…，rim（t））>0.5α并且min（ri1（t），ri2（t），…，rim（t））<-0.5α（α是预定义的阈值），则将第i个决策变量分类为多最优值变量。否则，第i个决策变量将被视为单最优值变量。

首先计算每个决策变量i与每个目标j之间的SRCC值，然后根据SRCC值将决策变量分为多最优值变量（第10行）或单最优值变量（第12行），然后采取上述对应方案。

Classification–变化响应中决策变量分类

在大多数现有的DMOPs中，考虑到环境变化，可以将决策变量分类为相似，可预测和不可预测的变量。

• 相似 —无需重新初始化
• 可预测 ----决策变量应基于预测进行重新初始化
• 不可预测 -----可以通过引入多样性进行重新初始化

非参数t-test用于评估决策变量的变化与环境变化的相关性

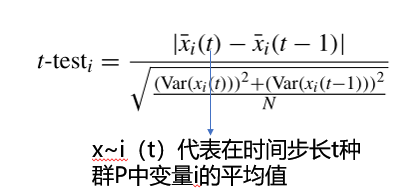
t-testi <=β，其中β是预定义的阈值，则第i个变量被视为无明显变化，也就是说，它是相似的变量，不需要重新初始化。如果t-testi>β，则第i个决策变量被认为具有显著变化，即变量i是可预测的或不可预测的，需要重新初始化。

上面公式已经区分了相似或者可预测和不可预测的情况，现在我们继续区分到底是可预测情况还是不可预测情况。如下图所示

将x_center的第i个决策变量置为预测值而其他决策变量保持不变来生成n个试验个体x_trial[i]，如果x_trial [i]支配x_center，则接受第i个决策变量的预测，并将第i个决策变量分类为可预测变量，并使用基于预测的方法重新初始化。否则，第i个决策变量是不可预测的，并使用基于多样性引入的方法重新初始化

下面就展示算法3 的伪代码

首先，分别根据（7）和（8）计算t-test和x_center。其次，使用预测模型来预测新的个体x_p（确切的预测模型在第IV -C节中进行了描述）。第三，产生试验个体（第6-14行）并进行评估。如果试验个体支配质心个体，则该试验个体的相应决策变量的预测是正确的，否则该预测是不可接受的。

B、环境选择

• DMOEA-DVC和SGEA[33]使用相同的选择方法，适应度函数F(i)表示支配个体xi的个体数目
  

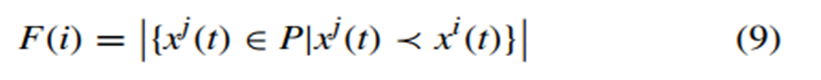
• 如果存档A中个体少于N则从种群中挑选最好的个体进P’，如果刚好相等，就将A中所有个体转入P’，如果存档A中个体多了就从种群中挑选最远的个体进P’.

C、ChangeResponse --变化响应

定义的三种类型的决策变量分别使用保持，多样性引入和预测方法。

• 保持：如果决策变量是相似变量，则DMOEA-DVC会在变化响应中保持该变量的值不变。
• 多样性引入：如果决策变量是不可预测的变量，则对该变量应用随机重新初始化策略。变量更新如下：
  
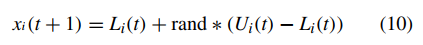
  其中，Li（t）和Ui（t）分别表示在时间t处第i个变量的上限和下限，rand是[0，1]中的随机值。
• 预测方法：如果将决策变量分类为可预测变量，则使用具有较短训练周期的卡尔曼滤波器[25]，[33]通过中心预测将其重新初始化。
• 
  下面就是算法4的伪代码
  

D、GenerateOffspring --子代生成

模拟二进制交叉（SBX）或DE交叉算子用于根据决策变量是否为多最优值变量来生成决策变量的值。SBX和DE交叉算子是MOEAs中两个常用的交叉算子。

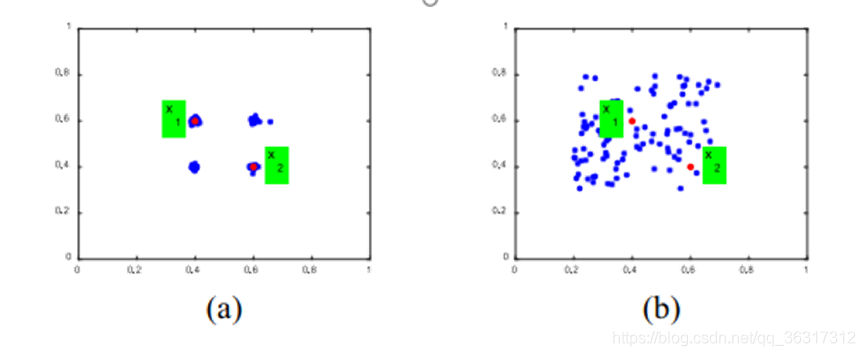
图1展示了这两个交叉算子生成的子代解的分布示例。SBX生成的子代解更接近父代，而DE交叉生成的子代解远离父代。应该在远离父代的位置生成多最优值变量，在这种情况下应使用DE交叉算子。而单最优值变量应在父代附近生成，即选择SBX。

这个伪代码已经很简单了，如果是多最优值变量就选择DE交叉算子，否则，单优值变量选择SBX交叉算子。

E、种群更新

DMOEA-DVC使用与SGEA相同的稳态种群更新策略。种群更新策略在父种群P和档案A中都执行。新生成的子代个体y用于替换P中最差的个体，同时更新A。

Conclusion

• 本文提出了一种基于决策变量分类的DMOEA，即DMOEA-DVC。对静态优化阶段和变化响应阶段的决策变量进行了分类。采用不同的策略来生成不同类型变量的值，以达到种群多样性和收敛性的良好平衡。
• DMOEA-DVC与其他六种最先进的DMOEA在33个基准DMOP上进行了比较。实验结果表明了DMOEA-DVC算法的有效性。

ps：上面大部分也是根据原文来进行总结以及理解的，由于本人也是才接触多目标进化没多久，学术功底有限，如果有不正确的地方欢迎批评指正！同时也借鉴了这些博客，如果想要了解，可以看
https://blog.csdn.net/u013555719/article/details/106856234?
同时这篇文章提到的几种动态多目标的算法，DCOEA、PPS、SGEA、有兴趣大家可以搜索了解一下。
同时我目前的微信公众号也是“研行笔录”，后期我也会持续更新，如果有兴趣的话，可以点个关注，不迷路！