【LeetCode 46】450.删除二叉搜索树的节点

【LeetCode 46】450.删除二叉搜索树的节点

一、题意

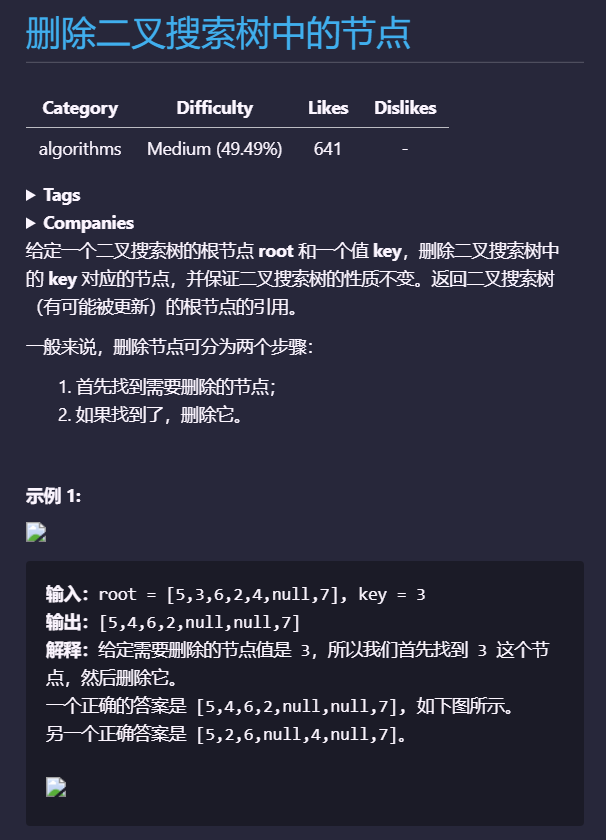
二、解答过程

二叉搜索树的删除要比插入困难，复杂。同样需要递归！

二叉搜索树删除情况有五种：

• 没找到删除的节点，遍历到空节点直接返回了
• 找到删除的节点
  • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
  • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
  • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
  • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

class Solution {
    
    
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
    
    
        //情况一：没有找到删除的节点，遍历到空节点直接返回
        if(root==NULL) return root;
        if(root->val==key)
        {
    
    
            //情况二：左右孩子都为空（叶子节点），直接删除节点，返回NULL为根节点
            //情况三：其左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
            if(root->left==NULL) return root->right;

            //情况四：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
            else if(root->right==NULL) return root->left;

            /*
            情况五：左右孩子节点都不为空，则将删除节点的左孩子放到删除节点的右子树
            树的最左面节点的左孩子的位置
            返回删除节点右孩子为新的根节点
            */
           else
           {
    
    
               TreeNode *tmp=root->right;
               while(tmp&&tmp->left)
               {
    
    
                   tmp=tmp->left;
               }
               swap(root->val,tmp->val);
                root->right=deleteNode(root->right,key);
           }
        }

        //被删除的节点key值在左子树，去左子树找就可以了（key值是我们要找的）
        if(root->val>key)
        {
    
    
            root->left=deleteNode(root->left,key);
        }
        //被删除的节点key值在右子树，去右子树找就可以
        if(root->val<key)
        {
    
    
            root->right=deleteNode(root->right,key);
        
        }
        return root;
    }
};