活动地址:CSDN21天学习挑战赛
作者简介:大家好我是小唐同学(๑><๑),为梦想而奋斗的小唐,让我们一起加油!!!
个人主页:小唐同学(๑><๑)的博客主页
系列专栏:数据结构
博友们如果也是新手入门数据结构我希望大家可以多加练习 数据结构题库在牛客网就有已经给大家附上链接,可以直接点击跳转:刷题点这里
牛客网支持ACM模式哦,刷算法题也很推荐哦!!!
下面上文章------》
目录
折半查找概念:
折半查找也称为二分查找,是一种效率比较高的查找算法,但是这是在该序列已经有序的状态下,因为该算法的核心思想就是缩小搜索区间,也要保持在元素不遗漏的状态下。
折半查找步骤:
1.输入:
(1)n个数(有序数列--升序)
(2)待查找元素
2.输出
查找成功:返回该元素在有序数列中的下标
查找失败:返回-1或自定义失败的标识
算法思想:
核心思想就是不断缩小搜索范围,在缩小范围时你会遇到三种情况
1.与目标值相等:直接返回对应下标,结束
2.比目标值大:因为数列有序 则中值元素在目标值的后边,搜索区间减半(在左一半),再算出减半后的区间的中值进行比较,以此类推。
3.比目标值小:由于元素有序,则中值元素在目标值的前边,搜索区间减半(在右一半),再算出减半后的区间的中值进行比较,以此类推。
如果区间两端点重合且端点值不相等则表示查找失败。
算法图解:
图片来自《数据结构简明教程》

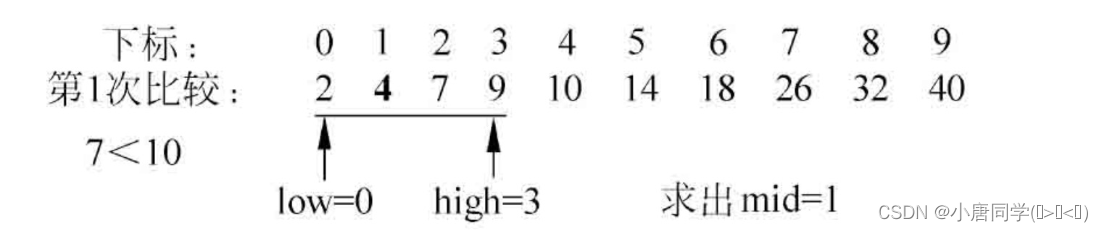

第一次查找:mid坐标为4,对应元素为10,大于7,则区间变为左一半:[0,3];
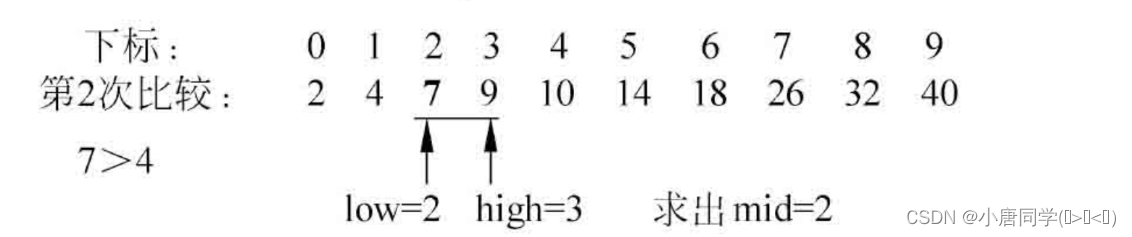
第二次查找:mid坐标为1,对应元素为1,小于7,则区间变为右一半:[0,3];
第三次查找:mid坐标为2,对应元素为7,等7,返回下标:mid+1=3;
代码实现:
# include <stdio.h>
int main()
{
int a[7];
int n;
printf("请输入要查找的元素");
scanf("%d",&n);
printf("请输入数组元素");
for(int i=0;i<7;i++)
{
scanf("%d",&a[i]);
}
//存储变化的区间右端点
int r=6;
//存储变化的区间左端点
int l=0;
int mid;
while(l<=r)
{
mid=(r+l)/2;
if(a[mid]==n)
{
printf("%d",mid);
return mid;
}
if(a[mid]<n)
{
l=mid+1;
}
if(a[mid]>n)
{
r=mid-1;
}
}
return -1;
}
时间复杂度分析:
(1)最坏情况:
最后一次才找到 设次数为t 因为每次缩小1/2 所以2^t=n;
则t=㏒₂n 则时间复杂度相当于对数级别O(㏒₂n )
(2)最好情况:
一次找到,则时间复杂度为常数级别O(1);
(3)平均情况:
综合则二分查找时间复杂度为O(㏒₂n )。
空间复杂度:
因为只需要几个固定变量则空间复杂度为常数级:O(1)。
