目录
激活函数的性质
- 连续并可导（允许少数点上不可导）的非线性函数。
可导的激活函数可以直接利用数值优化的方法来学习网格参数。
- 激活函数及其导数要尽可能的简单。
有利于提高网格计算效率。
- 激活函数的导函数的值域要在一个合适的区间内。
不能太大也不能太小，否则会影响训练的效率和稳定性。
- 单调递增
常见激活函数
常见激活函数包括：S型函数、斜坡函数和复合函数
S型激活函数
S型函数包括Logistic函数和tanh函数等
S型激活函数的性质：
- 两个函数都是梯度饱和函数，即在两端的梯度接近于0。
- Tanh函数是0中心化的，而logistic函数的输出恒大于0，非零中心化的输出使得最后一层的神经元的输入发生偏置偏移，并进一步使得梯度下降的收敛速度变慢。
斜坡函数
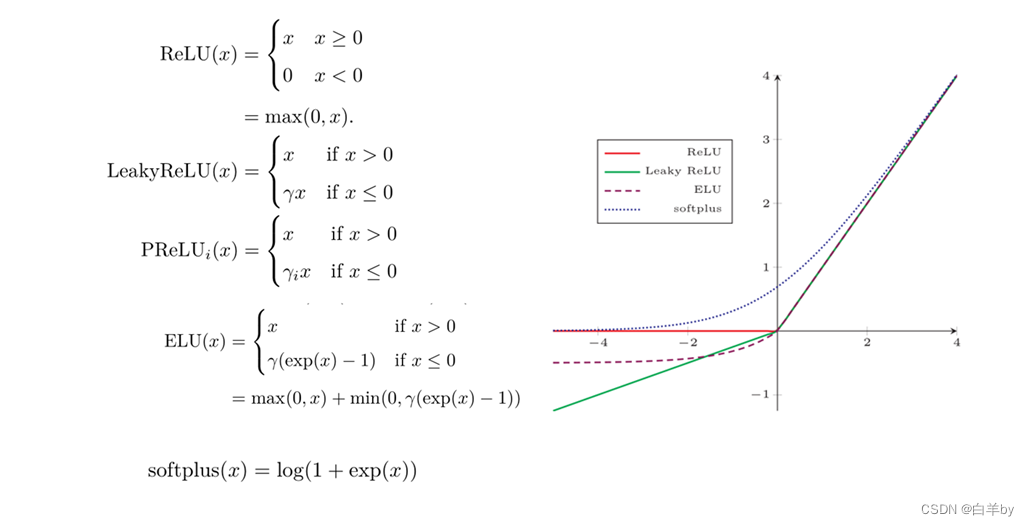
斜坡函数的性质：
- 计算更加高效。
- 生物学合理性：单侧抑制、宽兴奋边界。
- 在一定程度上缓解梯度消失问题。
复合函数
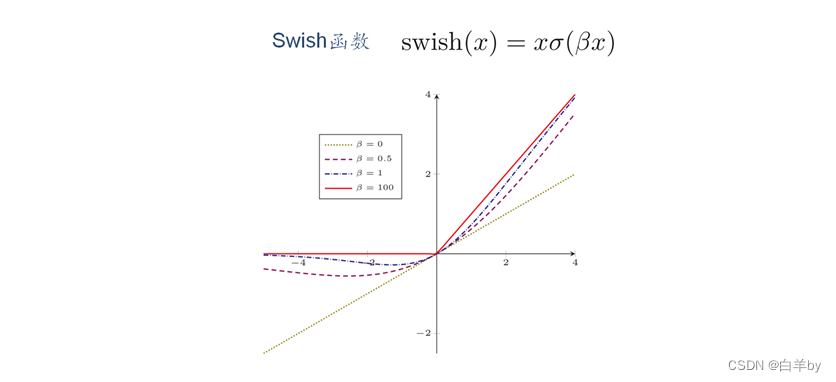
Swish函数性质：
- 和Relu一样没有上边界，因此不会出现梯度饱和现象。
- 有下边界，可以产生更强的正则化效果。
- 非单调。
- 处处连续可导，容易训练。
常见激活函数及其导数
