BF算法和KMP算法可以说是串中重要的算法,也是数据结构必学算法,我以前是不太理解KMP算法的,但是现在说来可以写出程序 理解思想了 也能懂了next数组,若有错误清在评论区指出,一起探讨。
一、BF算法
1.理解阶段
算法中最紧要的是理解一个算法的思想,就像是人一样,没有思想与行尸走肉无异,算法是一样的。BF算法的时间复杂度最理想为O(n) ------n为子串的长度
最不理想为O(n*m) ------------------m为主串长度
BF算法又称为简单模式匹配算法 其思想简单 容易理解 但是效率较低(需要回溯)
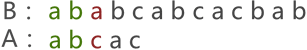
第一次进行模式匹配 匹配到第3个字符 匹配错误。
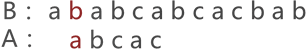
进行第2次模式匹配,本次匹配会把子串回溯到起点 主串会回溯到上次进行匹配的起点的下一个位置 可以看到到子串的第2个字符匹配失败 重新回溯
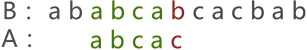
第3次进行模式匹配 同上回溯方法 到第5个字符匹配失败 重新回溯

第4次进行模式匹配 匹配成功
2.代码阶段
如果说理解重要,但是只处于理解阶段对于一个程序员是远远不够的,还要有代码能力。
先给出BF算法部分代码
我定义返回型为int型 返回第一次出现的位置
int creatBF(char *a,char *b)
{
//a主串 b子串
int i=0,j=0,x=0;
while(i<strlen(a)&&j<strlen(b)) //子串主串都没有到达最后 到达最后说明匹配不成功
{
if(a[i]==b[j])
{
i++;
j++;
}
else
{
i=x+1; //x存储上一次开始的起点
j=0; //回溯
x=i; //记录本次开始的起点
}
}
//跳出循环 则到达a的长度或到达b的长度
//到达a 则说明匹配成功
//到达b 则说明 匹配不成功
if(j==strlen(b))
{
return x;
}
return 0;
}测试结果如下:
二、KMP算法
1.理解阶段
KMP算法是BF算法的升级版 相对来说是 理解难度上升 但是效率得到了提高
KMP算法相对与BF算法 是主串不需要回溯 子串是回溯到特定的位置 可以有效减少比较次数
较少运行时间 提高效率
子串回溯 主要看next数组 ,我的理解是next数组是next数组的值-1表示最长前缀的下标


当子串主串发生失配时 主串不发生回溯,子串会回溯到最长相等前后缀数值的位置
而记录最长相等前后缀的就时next数组 next[j]=k 表示子串中前j-1个字符的最长相等前后缀长度为k-1
下面给出获得next数组的代码
1.next数组的获得代码
void GetNext(char *a,int next [])
{
//a主串 b子串
int j=0; //便利子串
int k=-1; //k时子串中每个字符的next值
next[0]=-1;
while(j<strlen(a))
{
if(k==-1||a[j]==a[k])
{
j++;
k++;
next[j]=k;
}
else
k=next[k];
}
}测试结果如图:
2.KMP算法代码如下:
KMP算法的核心在于求next数组 剩下的就是进行比较
int creatKMP(char *a,char *b,int next[])
{
//a 主串 b子串
int i=0,j=0;
while(i<strlen(a)&&j<strlen(b))
{
if(j==-1||a[i]==b[j])
{
i++;
j++;
}
else
j=next[j];
}
if(j>=strlen(b))
{
return (i-strlen(b));//i表示 查找结束在主串中的位置减去子串长度 为首位置
}
else
return -1;
} 测试结果如图:
下面我会给出完整的程序,包括BF和KMP算法 如下:
# include <stdio.h>
#include <string.h>
void GetNext(char *a,int next [])
{
//a主串 b子串
int j=0; //便利子串
int k=-1; //k时子串中每个字符的next值
next[0]=-1;
while(j<strlen(a))
{
if(k==-1||a[j]==a[k]) //表示判断加入后缀 j后是否与会 使最长前后缀增加 a[k] 表示最长前缀的后一个
{
j++;
k++;
next[j]=k;
}
else
k=next[k];
}
}
int creatKMP(char *a,char *b,int next[])
{
//a 主串 b子串
int i=0,j=0;
while(i<strlen(a)&&j<strlen(b))
{
if(j==-1||a[i]==b[j])
{
i++;
j++;
}
else
j=next[j];
}
if(j>=strlen(b))
{
return (i-strlen(b));//i表示 查找结束在主串中的位置减去子串长度 为首位置
}
else
return -1;
}
int creatBF(char *a,char *b)
{
//a主串 b子串
int i=0,j=0,x=0;
while(i<strlen(a)&&j<strlen(b)) //子串主串都没有到达最后 到达最后说明匹配不成功
{
if(a[i]==b[j])
{
i++;
j++;
}
else
{
i=x+1; //x存储上一次开始的起点
j=0; //回溯
x=i; //记录本次开始的起点
}
}
//跳出循环 则到达a的长度或到达b的长度
//到达a 则说明匹配成功
//到达b 则说明 匹配不成功
if(j==strlen(b))
{
return x;
}
return 0;
}
int main()
{
char a[13];
char b[5];
scanf("%s%s",a,b);
int t=creatBF(a,b);
printf("%d\n",t);
int next[5];
GetNext(b,next);
//for(int i=0;i<5;i++)
//{
// printf("%d ",next[i]);
//}
int y=creatKMP(a,b,next);
printf("%d",y);
}三.BF算法与KMP算法的区别与优缺点
BF算法是子串主串都需要进行回溯比较浪费时间,效率比较低。
KMP算法是主串不需要回溯,子串只需要根据next数组进行回溯到特定位置