数理统计（一）——统计量

期望

1. 期望可以简单理解为概率加权下的“平均值”，即试验中每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的大小：
   
   1. 离散型： $$E(X)=\sum_ix_ip_i$$
   2. 连续型： $$E(X)=\int_{-\infty}^{\infty}xf(x)dx$$
2. 期望的性质：
   
   1. 无条件存在：
      
      1. $E(kX) = kE(X)$
      2. $E(X+Y) = E(X) + E(Y)$
   2. 若X和Y 相互独立 ：$E(XY)=E(X)E(Y)$（反之不成立，即$E(XY)=E(X)E(Y)$是X和Y相互独立的必要不充分条件）

方差

1. 定义：$Var(X)=E\{[X-E(X)]^2\}=E(x^2)-E^2(X)$ （方差恒大于等于0）
   
   1. $E\{[X-E(X)]^2\} \ge 0 \Longrightarrow E(x^2) \ge E^2(X)$，当$X$为定值时，取等号
2. 方差的性质：
   
   1. 无条件成立：
      
      1. $Var(C) = 0 (C是常数)$
      2. $Var(X + C) = Var(X)$
      3. $Var(kX) = k^2Var(X)$
   2. 若$X$和$Y$ 独立：
      
      1. $Var(X+Y) = Var(X) + Var(Y)$
3. 方差代表了数据的震荡程度

标准差

方差的平方根就是标准差

协方差

1. 协方差：
   
   1. 定义：$Cov(X,Y) = E\{[X-E(X)][Y-E(Y)]\}$
   2. 性质：
      
      1. $Cov(X,Y) = Cov(Y,X)$
      2. $Cov(aX+b, cY+d) = acCov(X,Y)$
      3. $Cov(X_1+X_2,Y) = Cov(X_1, Y) + Cov(X_2, Y)$
      4. $Cov(X,Y) = E(XY)-E(X)E(Y)$

协方差和独立不相关

当$X$和$Y$独立时，$E(XY)=E(X)E(Y)$而$Cov(X,Y)=E(XY)-E(X)E(Y)$，从而，当$X,Y$独立时，$Cov(X,Y)=0$；
但反过来不一定成立，即$Cov(X,Y)=0$只能得到$X,Y$不相关

协方差的意义

协方差是两个随机变量具有相同方向变化趋势的度量，：
1. 若$Cov(X,Y)>0$，则它们的变化趋势相同；
2. 若$Cov(X,Y)<0$，则它们的变化趋势相反；
3. 若$Cov(X,Y)=0$，则它们不相关
即，如果协方差为正，说明X,Y同向变化，协方差越大说明同向程度越高；如果协方差为负，说明X,Y反向变化，协方差越小说明反向程度越高
详细解释可查看协方差的意义

协方差的上界

1. $Cov(X,Y) = E{[X-E(X)][Y-E(Y)]}$
2. $|Cov(X,Y)| = |E{[X-E(X)][Y-E(Y)]}|$
3. 由柯西不等式得：$|E{[X-E(X)][Y-E(Y)]}| \le \sqrt{E\{[X-E(X)]^2\}}\sqrt{E\{[Y-E(Y)]^2\}}$
4. 即$Cov(X,Y) \le \sqrt{Var(X)}\sqrt{Var(Y)}$
5. 柯西不等式：$|E(XY)| \le \sqrt{E(X^2)}\sqrt{E(Y^2)}$

协方差矩阵

对于n个随机向量$(X_1,X_2,...,X_n)$，任意两个元素$X_i,X_j$都可以得到一个协方差，从而形成$n*n$的矩阵；协方差矩阵是对称阵
$c_{ij}=E{[X_i-E(X_i)][X_j-E(X_j)]}=Cov(X_i,X_j)$

$$\left [ \begin{matrix} c_{11} & c_{12} & ... & c_{1n} \\ c_{21} & c_{22} & ... & c_{2n} \\ ...\\ c_{n1} & c_{n2} & ... & c_{nn} \\ \end{matrix} \right ]$$

独立和不相关

独立一定不相关,不相关不一定独立

Pearson相关系数

1. 定义：$\rho_{xy}=\frac{Cov(X,Y)}{\sqrt{Var{X}}\sqrt{Var(Y)}}$
2. pearson是一个介于-1和1之间的值，当两个变量的线性关系增强时，相关系数趋于1或-1；当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；如果相关系数等于0，表明它们之间不存在线性相关关系。
3. 也可以将Pearson相关系数理解为余弦相似度在维度缺失下的一种改进，余弦相似度公式：$\cos<x,y>=\frac{xy}{|x||y|}$，Pearson相关系数计算公式：皮尔逊系数就是cos计算之前两个向量都先进行中心化(centered)

详细介绍请看这儿

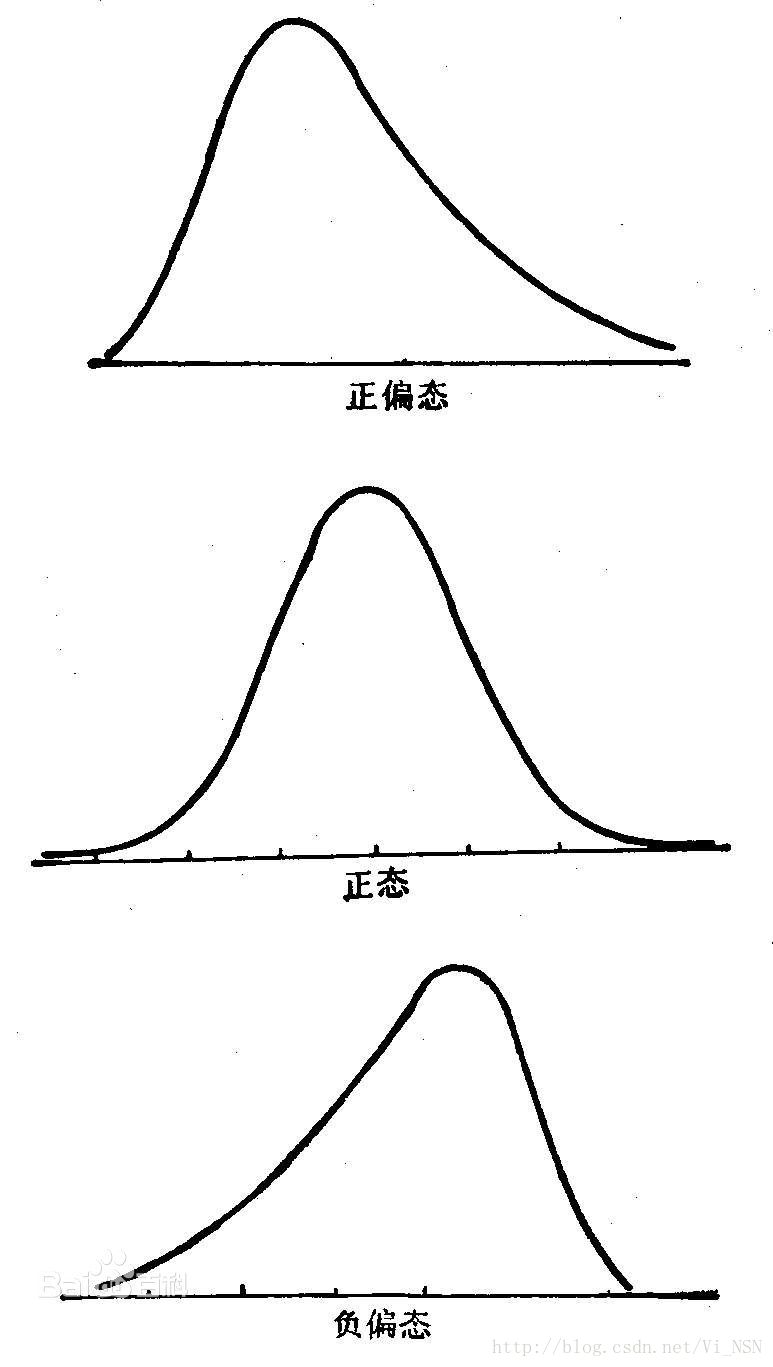
偏度

1. 定义：
   
   1. 偏度（skewness），是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。偏度(Skewness)亦称偏态、偏态系数。
   2. 表征概率分布密度曲线相对于平均值不对称程度的特征数。直观看来就是密度函数曲线尾部的相对长度。
   3. 定义上偏度是样本的三阶标准化矩，定义式如下，其中$k_2、k_3$ 分别表示二阶和三阶中心矩： $$Skew(X)=E[(\frac{X-\mu}{\sigma})^3]=\frac{k_3}{\sigma^3}=\frac{k_3}{k_2^{\frac{3}{2}}}$$
2. 性质：正态分布的偏度为0，两侧尾部长度对称。若以bs表示偏度。bs<0称分布具有负偏离，也称左偏态，此时数据位于均值左边的比位于右边的少，直观表现为左边的尾部相对于与右边的尾部要长，因为有少数变量值很小，使曲线左侧尾部拖得很长；bs>0称分布具有正偏离，也称右偏态，此时数据位于均值右边的比位于左边的少，直观表现为右边的尾部相对于与左边的尾部要长，因为有少数变量值很大，使曲线右侧尾部拖得很长；而bs接近0则可认为分布是对称的。若知道分布有可能在偏度上偏离正态分布时，可用偏离来检验分布的正态性。右偏时一般算术平均数>中位数>众数，左偏时相反，即众数>中位数>平均数。正态分布三者相等。

峰度

1. 定义：
   
   1. 峰度（peakedness;kurtosis）又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量，如果峰度大于三，峰的形状比较尖，比正态分布峰要陡峭。反之亦然。
   2. 在统计学中，峰度（Kurtosis）衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。
2. 峰度的类型：
   
   1. 尖顶峰度：当变量值的次数在众数周围分布比较集中，使次数分布曲线比正态分布曲线顶峰更为隆起尖峭，称为尖顶峰度
   2. 平顶峰度：当变量值的次数在众数周围分布较为分散，使次数分布曲线较正态分布曲线更为平缓，称为平顶峰度
   3. 标准峰度：即正态分布峰度。尖顶峰度或平顶峰度都是相对正态分布曲线的标准峰度而言的。
3. 计算：
   
   1. 通常定义四阶中心矩除以方差的平方减3为峰度值，即 $$\gamma_2=\frac{k_4}{k_2^2}=\frac{\mu_4}{\sigma^4}-3=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline x)^4}{(\frac{1}{n}\sum_{i=1}^n(x_i-\overline x)^2)^2}-3$$
   2. $\frac{\mu_4}{\sigma^4}$也被称为超值峰度
      
      1. 减3是为了让正态分布的峰度为0；
      2. 超值峰度为正，称为尖峰态；
      3. 超值峰度为负，称为低峰态
   3. 将$\mu_4$除以其标准差的四次方$σ^4$，目的是消除单位量纲的影响，便于不同次数分布曲线的峰度比较，从而得到以无名数表示的相对数，即为峰度的测定值

矩

1. 定义：
   
   1. 对于随机变量X，X的k阶原点矩为$E(X^k)$
   2. $X$的$k$阶中心矩为$E\{[X-E(X)]^k\}$
2. 统计参数总结：
   
   1. 期望：一阶原点矩；
   2. 方差：标准差、二阶中心矩；
   3. 变异系数(Coefficient of Variation)：标准差与均值的比值称为变异系数，记为$C\cdot V$
   4. 偏度(Skewness)：三阶
   5. 峰度(Kurtosis)：四阶