2022 高教社杯(国赛数学建模)思路解析
2022高教社杯ABCD赛题思路解析:
https://blog.csdn.net/dc_sinor/article/details/126211983
1 啤酒和尿布
Apriori算法是一种用于挖掘数据集内部关联规则的算法,“apriori”在拉丁语中翻译为“来自以前”,听意思你应该就能猜到了,这个算法是用先验知识来预测数据的关联规则的。
说到关联规则,有一个很有名的案例——啤酒与尿布。说,美国一家连锁店发现很多男性会在周四购买尿布和啤酒,这两种看似不相干的商品之间显现出强相关性,于是商家可以将啤酒货架放在尿布货架旁边以增加收益。
那么,啤酒与尿布的关系是如何被发现的呢?当然是通过关联算法,我们从Apriori算法开始吧,利用Apriori进行关联分析。
2 Apriori原理
先介绍两个概念
- 支持度support:数据集中包含该项集的数据所占数据集的比例,度量一个集合在原始数据中出现的频率
- 置信度confidence:是针对一条关联规则来定义的,a->b的置信度=支持度{a|b}/支持度{a},a|b表示ab的并集
关联分析有两个目标:
- 发现频繁项集(频繁项集是满足最小支持度要求的项集,它给出经常在一起出现的元素项)
- 发现关联规则(关联规则意味着元素项之间“如果…那么…”的关系)
Apriori原理
如果某个项集是频繁的,那么它的所有子集也是频繁的
如果某个项集是非频繁的,那么它的所有超集也是非频繁的
基于此,Apriori算法从单元素项集开始,通过组合满足最小支持度的项集来形成更大的集合
其实Apriori就是通过排除法来选择频繁项集和关联规则,下面我们根据这样的原理用python实现算法。
3 Apriori代码实现
3.1 挖掘频繁项集
挖掘频繁项集的逻辑如下图
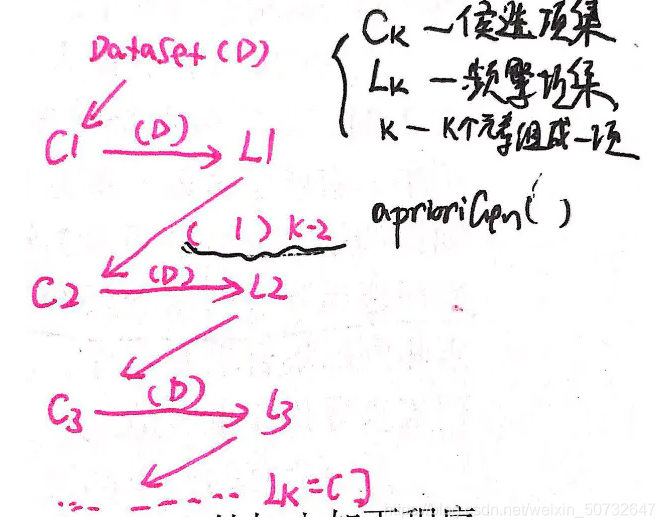
#加载数据集
def loadDataSet():
return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
#选取数据集的非重复元素组成候选集的集合C1
def createC1(dataSet):
C1=[]
for transaction in dataSet: #对数据集中的每条购买记录
for item in transaction: #对购买记录中的每个元素
if [item] not in C1: #注意,item外要加上[],便于与C1中的[item]对比
C1.append([item])
C1.sort()
return list(map(frozenset,C1)) #将C1各元素转换为frozenset格式,注意frozenset作用对象为可迭代对象
#由Ck产生Lk:扫描数据集D,计算候选集Ck各元素在D中的支持度,选取支持度大于设定值的元素进入Lk
def scanD(D,Ck,minSupport):
ssCnt={
}
for tid in D: #对数据集中的每条购买记录
for can in Ck: #遍历Ck所有候选集
if can.issubset(tid): #如果候选集包含在购买记录中,计数+1
ssCnt[can]=ssCnt.get(can,0)+1
numItems=float(len(D)) #购买记录数
retList=[] #用于存放支持度大于设定值的项集
supportData={
} #用于记录各项集对应的支持度
for key in ssCnt.keys():
support=ssCnt[key]/numItems
if support>=minSupport:
retList.insert(0,key)
supportData[key]=support
return retList,supportData
#由Lk产生Ck+1
def aprioriGen(Lk,k): #Lk的k和参数k不是同一个概念,Lk的k比参数k小1
retList=[]
lenLk=len(Lk)
for i in range(lenLk):
for j in range(i+1,lenLk): #比较Lk中的每一个元素与其他元素
L1=list(Lk[i])[:k-2];L2=list(Lk[j])[:k-2]
L1.sort();L2.sort()
if L1==L2: #若前k-2项相同,则合并这两项
retList.append(Lk[i]|Lk[j])
return retList
#Apriori算法主函数
def apriori(dataSet,minSupport=0.5):
C1=createC1(dataSet)
D=list(map(set,dataSet))
L1,supportData=scanD(D,C1,minSupport)
L=[L1]
k=2
while len(L[k-2])>0: #当L[k]为空时,停止迭代
Ck=aprioriGen(L[k-2],k) #L[k-2]对应的值是Lk-1
Lk,supK=scanD(D,Ck,minSupport)
supportData.update(supK)
L.append(Lk)
k+=1
return L,supportData
我们来测试一下
dataset=loadDataSet()
C1=createC1(dataset)
D=list(map(set,dataset))
L1,supportData0=scanD(D,C1,0.5)
L,supportData=apriori(dataset,minSupport=0.5)

可以看到,频繁项集如上图,{1,2,3,5,{2,3},{3,5},{2,5},{1,3},{2,3,5}}都是频繁项集。得到了频繁项集,接下来我们看看频繁项集之间的关联规则。
3.2 从频繁项集挖掘关联规则
挖掘关联规则原理如下:若某条规则不满足最小置信度要求,则该规则的所有子集也不满足最小置信度要求
# 主函数,由频繁项集以及对应的支持度,得到各条规则的置信度,选择置信度满足要求的规则为关联规则
# 为了避免将所有数据都对比一遍,采用与上述相同的逻辑减少计算量——一层一层计算筛选
def generateRules(L,supportData,minConf=0.7):
bigRuleList=[]
for i in range(1,len(L)):
for freqSet in L[i]:
H1=[frozenset([item]) for item in freqSet] # H1是频繁项集单元素列表,是关联规则中a->b的b项
if i>1:
rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
else:
calConf(freqSet,H1,supportData,bigRuleList,minConf)
return bigRuleList
# 置信度计算函数
def calConf(freqSet,H,supportData,brl,minConf=0.7):
prunedH=[] # 用于存放置信度满足要求的关联规则的b项,即“提纯后的H”
for conseq in H:
conf=supportData[freqSet]/supportData[freqSet-conseq]
if conf>=minConf:
print (freqSet-conseq,'-->',conseq,'conf:',conf)
brl.append([freqSet-conseq,conseq,conf])
prunedH.append(conseq)
return prunedH
# 关联规则合并函数
def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):
m=len(H[0])
if len(freqSet)>(m+1): #查看频繁项集freqSet是否大到可以移除大小为m的子集
Hmp1=aprioriGen(H,m+1) # 从Hm合并Hm+1
Hmp1=calConf(freqSet,Hmp1,supportData,brl,minConf)
if len(Hmp1)>1: #若合并后的Hm+1的元素大于1个,则继续合并
rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)
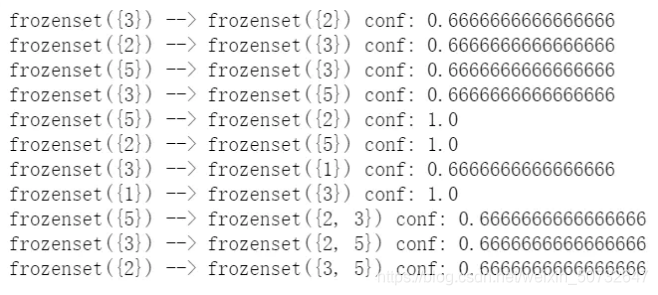
可以看到,如果有5那么必定有2,如果有3,那么66.7%的可能性有2,5……
3.3 总结
本文简述关联分析算法Apriori算法的原理,然后用python3进行了实操,需要注意的是,Apriori算法的缺点——每次增加频繁项集大小时(即Ck->Lk时),算法需要重新扫描整个数据集,当数据集很大时,算法效率很低。
解决方法是FP-Growth算法,这个算法我们下一次讲解。
2022 高教社杯(国赛数学建模)思路解析
2022高教社杯ABCD赛题思路解析:
https://blog.csdn.net/dc_sinor/article/details/126211983