一、朴素贝叶斯
1.原理
公式原型: (贝叶斯公式)
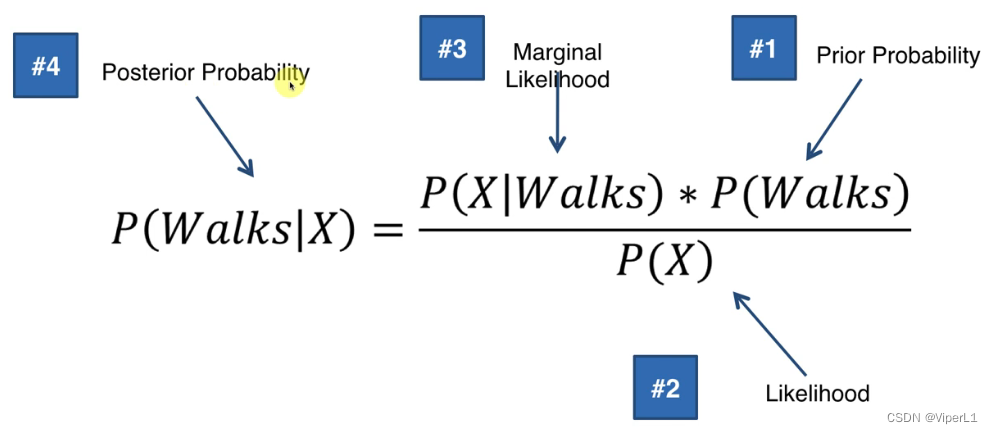
求出两个可能性然后进行对比。
#1:事件发生的全局概率(=发生的事件/总事件)
#2:事件发生的局部概率(=局部内发生的事件/局部内总事件--贴近新的样本)

#3:已知事件坐落与数据空间内的概率(=局部内发生的事件/总事件发生的事件)

#4:利用已知数据求得最终概率
Attention:
①先决条件:假定所有事件的概率都是独立的,
②P(X):在比较的时候可以约掉P(X),但是计算的值将不再是后验概率

③已知组大于两类的情况:将所有后验概率计算出来进行比较
2.Python实现
①使用分类器模板
②创建分类器并拟合
from sklearn.naive_bayes import GaussianNB --导入朴素贝叶斯分类器
classifier=GaussianNB() --新建类型
classifier.fit(x_train,y_train) --拟合
③进行预测并展示图线
pred = classifier.predict(x_test) --进行预测
--调用展示模板

二、决策树
1.原理
类别:分类决策树(按类别划分--分类组之间无序)
回归决策树(连续数据--数据之间有序)
分类决策树原理:对平面进行不断分割(直至所有类被分开)

关键:寻找分割线(目的:提升熵)
流程图:划分决策树的步骤(不一定要完全分割--可以用概率表示)

2.Python实现
①使用分类器模板
②创建和拟合分类器
--由于没有使用欧氏距离,所以不需要特征缩放
from sklearn.tree import DecisionTreeClassifier --导入库
classifier = DecisionTreeClassifier(criterion = 'entropy',random_state=0)
--参数:基尼系数/熵,随机数
classifier.fit(x_train,y_train) --拟合③预测和图线展示
y_pred = classifier.predict(x_test)
错误的分类被称为噪音。过度拟合时会被噪音干扰

三、随机森林
1.原理
采用多个分类器对数据进行学习,再采用方法(加权/投票)将结果组合
Step1:装袋--随机采用K个训练集的数据,将其装袋
Step2:用装袋的数据,训练分类器
Step3:重复Step1-Step2,直到拥有足够的分类器
Step4:使用这些分类器单独预测,并进行投票
2.Python实现
①套用分类器模板
②创建分类器并拟合
from sklearn.ensemble import RandomForestClassifier --导入类
classifier = RandomForestClassifier(h_estimators=10,criterion='entropy',random_state=0)
--估计量(决策树数量),标准(基尼指数/熵)
classifier.fit(x_train,y_train)③预测和图线输出
y_pred = classifier.predict(x_test) --预测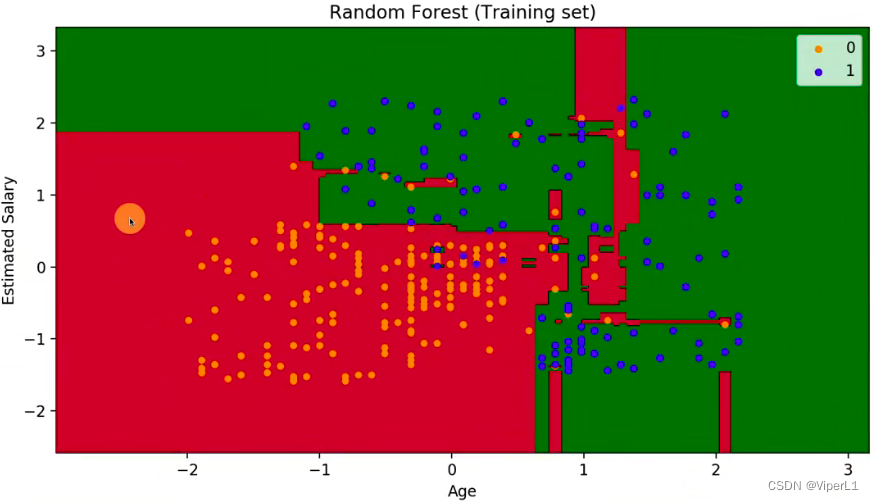
对比实际测试结果
