典型相关分析(CCA)及其python实现

典型相关分析(Canonical Correlation Analysis)是一种分析多变量与多变量之间关系的统计方法。比如我们现在有自变量$(x_1,x_2,x_3)=($身高，体重，肺活量$)$，因变量$(y_1,y_2)=(50$米成绩，立定跳远成绩$)$，我们想要研究自变量对因变量的作用。如果分别求取$x_i$对$y_j$的相关系数，在变量个数较多时比较麻烦。CCA与主成分分析的思想（见上一篇文章）类似，它利用原变量的线性组合来简化分析。

基本思想

设$n$维自变量$X=(x_1,x_2,...,x_n)$，$m$维因变量$Y=(y_1,y_2,...,y_m)$,我们想确定若干对典型相关变量$(U_i,V_i)$，使得

$U_i=a_{i1}{x}_1+a_{i2}{x}_2+...+a_{in}{x}_n$
$V_i=b_{i1}{y}_1+b_{i2}{y}_2+...+b_{im}{y}_m$

之间有最大的相关系数。此外，不同组的典型相关变量对之间应该不相关，即

$\rho (U_i,V_j)=0(i\ne j).$

约定$U_i,V_i$均为标准化变量，即

$var(U_i)=var(V_i)=1,$其中$var(X)$为$X$的方差。

求解过程

$1.设X为标准化后的自变量样本矩阵\left(\begin{array}{ccc}{x}_{11}& \cdots & x_{1t}\\ ⋮& & ⋮\\ x_{n1}& \cdots & x_{nt}\end{array}\right),其中n为自变量维数,t为样本数;$
$2.设Y为标准化后的因变量样本矩阵\left(\begin{array}{ccc}{y}_{11}& \cdots & y_{1t}\\ ⋮& & ⋮\\ y_{m1}& \cdots & y_{mt}\end{array}\right),其中m为因变量维数,t为样本数;$
$3.计算A=\left(\begin{array}{c}X\\ Y\end{array}\right)的协方差矩阵Cov(A);$
$4.设Cov(A)=\left(\begin{array}{cc}{R}_{11}& R_{12}\\ R_{21}& R_{22}\end{array}\right),其中R_{11}为n\times n矩阵，R_{22}为m\times m矩阵，R_{12}和R_{21}分别为n\times m和m\times n矩阵;$
$5.令M=R_{11}^{-1}{R}_{12}{R}_{22}^{-1}{R}_{21},计算M的所有正特征值{\lambda }_1,{\lambda }_2,...,{\lambda }_s(默认已经从大到小排序);$
$6.设{\alpha \alpha }_i为M的对应特征值{\lambda }_i的特征向量，k=1/\sqrt{{\alpha \alpha }_i^T{R}_{11}{\alpha \alpha }_i},将{\alpha \alpha }_i乘以k;$
$7.令{\beta \beta }_i=R_{22}^{-1}{R}_{21}{\alpha \alpha }_i/{\rho }_i,其中{\rho }_i={\sqrt{\lambda }}_i即为第i对典型变量的相关系数;$
$8.{\alpha \alpha }_i,{\beta \beta }_i即为自变量和因变量各个变量前的系数(已经标准化).$

说明：
$(1)$在第$4$步中，$R_{ij}$代表协方差矩阵，$1$为自变量，$2$为因变量;
$(2)$第$6$步将特征向量乘以$k$是为了标准化典型变量（注意是直接乘在${\alpha \alpha }_i$上的）。

经过上述过程，我们求出了三个我们关心的参数:${\alpha \alpha }_i,{\beta \beta }_i和{\rho }_i(i=1,2,...,s)$.

证明过程很多资料都已经给出了（见最后参考材料部分），这里不再证明。

python实现

这里采用参考材料3（ppt）中的一个例子，要分析$x_1,x_2,x_3$与$y_1,y_2,y_3$的关系，下面我们用python来实现一下：

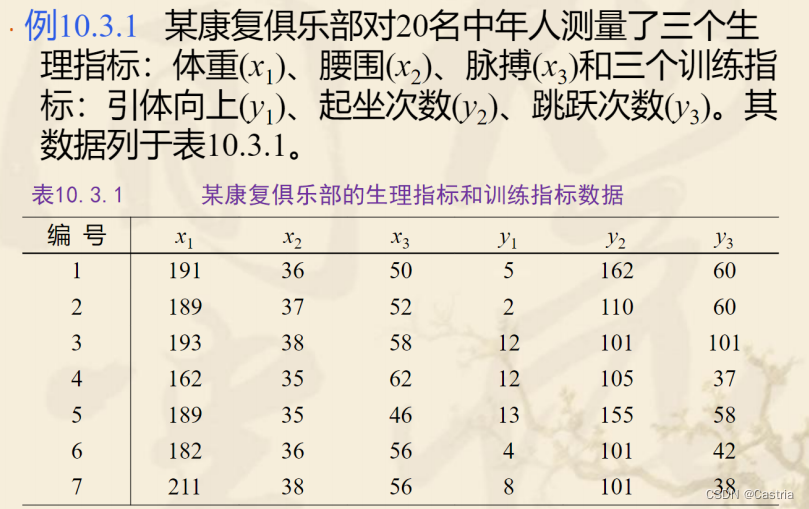
样本一共20组，代码中再给出。

from math import sqrt
import numpy as np

class CCA:

    '''
    # 说明
    该类用于典型相关分析。
    # 参数
    x_dataset 自变量数据，以[样本1, 样本2, ..., 样本t] 给出。

    y_dataset 因变量数据，以[样本1, 样本2, ..., 样本t] 给出。
    
    x_dataset 和 y_dataset 的样本应该一一对应。(第i个自变量决定第i个因变量)
    '''
    def __init__(self, x_dataset, y_dataset):
    	# 需要对数据转置一下，才能跟上文对上
        self.x_dataset = np.array(x_dataset, dtype = 'float64').T
        self.y_dataset = np.array(y_dataset, dtype = 'float64').T

    '''
    结果以三元组(rho, alpha, beta)形式给出:

        - rho: 典型变量的相关系数
        - alpha: 自变量系数
        - beta: 因变量系数
    '''
    def fit(self):
        A = []
        for sample in self.x_dataset:
            A.append(list(sample))
        for sample in self.y_dataset:
            A.append(list(sample))
        
        # 构造上面提到的A矩阵
        A = np.array(A, dtype = 'float64')
        
        # 标准化: 减去每行均值再除以标准差 
        for i in range(A.shape[0]):
            avg = np.mean(A[i])
            std = np.std(A[i])
            A[i] = (A[i] - avg) / std

		# bias = True 即计算时不采用对方差的无偏修正（除以n-1,样本方差）
		# 这里只是为了跟ppt里的数据对上,实际可以取消这个可选参数
        Cov = np.cov(A, bias = True)
        n = self.x_dataset.shape[0]

        R_11 = np.matrix(Cov[:n, :n])
        R_12 = np.matrix(Cov[:n, n:])
        R_21 = np.matrix(Cov[n:, :n])
        R_22 = np.matrix(Cov[n:, n:])

        M = np.linalg.inv(R_11) * R_12 * np.linalg.inv(R_22) * R_21
        N = np.linalg.inv(R_22) * R_21 * np.linalg.inv(R_11) * R_12

        eig1, vector1 = np.linalg.eig(M)

        data = []

        for i in range(len(eig1)):
        	# 若为0（精度误差，改为"绝对值小于一个很小的值"）
            if abs(eig1[i]) < 1e-10:
                continue
            # 下面变量与上面步骤中的意义相同
            rho = np.round(sqrt(eig1[i]), decimals = 5)
            alpha = np.round(vector1[:, i], decimals = 5)
            k = 1 / (alpha.T * R_11 * alpha)
            alpha *= sqrt(k)
            beta = np.round(np.linalg.inv(R_22) * R_21 * alpha / rho, decimals = 5)

            # 三元组分别为相关系数, 自变量系数, 因变量系数
            data.append((rho, alpha, beta))
        
        data.sort(key = lambda x: x[0], reverse = True)

        return data      

结果：

# 为了便于观察做了格式调整
[
(0.79561,    # 第一对典型变量
array([[ 0.7753969 ],[-1.5793479 ],[ 0.05911508]]),    # 自变量系数(第一对)
array([[ 0.3495 ],[ 1.05401],[-0.71642]])),            # 因变量系数(第一对)
(0.20056,    # 第二对
array([[-1.88437283],[ 1.18065335],[-0.23110043]]),
array([[-0.37555],[ 0.12347],[ 1.06216]])),
(0.07257,    # 第三对
array([[-0.19098071],[ 0.50601614],[ 1.05078388]]),
array([[-1.29659],[ 1.23682],[-0.41883]]))
]

结论：
我们得到了第一对典型变量
$U_1=0.7754x_1-1.5793x_2+0.0591x_3$
$V_1=0.3495y_1+1.054y_2-0.7164y_3$,
且它们的相关系数${\rho }_1=0.79561$，是高度相关的。此外，$x_2$即腰围的系数为$-1.5793,$是绝对值最大的，说明腰围对成绩会有很大影响；$x_3$即脉搏的系数仅为$0.059$,它的贡献比较低，说明脉搏这个自变量对成绩的影响可能不太大。可以类似地分析其它结果。如果一对典型变量不足以说明，还可以取第二对${\rho }_2=0.20056$继续分析。

参考材料

1.https://blog.csdn.net/weixin_44333889/article/details/119379776
2.https://zhuanlan.zhihu.com/p/372774724
3.https://max.book118.com/html/2019/0828/5343340333002121.shtm（这里提供该ppt的下载。）