摘要
随着云计算和人工智能的兴起,如何安全有效地利用数据,对持有大量数字资产的企业来说至关重要。同态加密,是解决云计算和分布式机器学习中数据安全问题的关键技术,也是隐私计算中,横跨多方安全计算,联邦学习和可信执行环境多个技术分支的热门研究方向。
本文对经典同态加密算法Pailier算法及其相关技术进行介绍,重点分析了Paillier的实现原理和性能优化方案,同时对基于公钥的加密算法中的热门算法进行了横向对比。最后介绍了Paillier算法的一些实际应用。
【关键词】:同态加密,多方安全计算,联邦学习,隐私计算
1 背景知识
1.1 同态加密
同态加密(Homomorphic Encryption,HE)[1] 是将数据加密后,对加密数据进行运算处理,之后对数据进行解密,解密结果等同于数据未进行加密,并进行同样的运算处理。同态加密的概念最初在1978年,由Ron Rivest,Leonard Adleman和Michael L. Dertouzos共同提出,旨在解决在不接触数据的前提下,对数据进行加工处理的问题。
目前,同态加密支持的运算主要为加法运算和乘法运算。按照其支持的运算程度,同态机密分为半同态加密(Partially Homomorphic Encryption, PHE)和全同态加密(Fully Homomorphic Encryption, FHE)。半同态加密在数据加密后只持加法运算或乘法运算中的一种,根据其支持的运算的不同,又称为加法同态加密或乘法同态加密。半同态加密由于机制相对简单,相对于全同态加密技术,拥有着更好的性能。全同态加密对加密后的数据支持任意次数的加法和乘法运算。
1.2 复合剩余类问题
如果存在一个数 y ∈ Z n 2 ∗ y∈\mathbb{Z}_{n^2}^\ast y∈Zn2∗, 那么符合公式 z ≡ y n ( m o d n 2 ) z ≡ y^n\ (mod\ n^2) z≡yn (mod n2)的数z,称为y的模 n 2 n^2 n2的n阶剩余。复合剩余类问题(decisional composite residuosity assumption , DCRA),指的是给定一个合数n和整数z,很难确定模 n 2 n^2 n2的n阶剩余数z是否存在。
1.3 中国剩余定理
中国剩余定理(Chinese Remainder Theorem, CRT),又称为孙子定理,源于《孙子算经》,是数论中的一个关于一元线性同余方程组的定理,说明了一元线性同余方程组有解的准则以及求解方法。
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
翻译为数学语言为:
{ x ≡ 2 ( m o d 3 ) x ≡ 3 ( m o d 5 ) x ≡ 2 ( m o d 7 ) \left\{ \begin{aligned} x ≡ 2 (mod{\,}{\,}3) \\ x ≡ 3 (mod{\,}{\,}5) \\ x ≡ 2 (mod{\,}{\,}7) \end{aligned} \right. ⎩ ⎨ ⎧x≡2(mod3)x≡3(mod5)x≡2(mod7)
其通用方程为:
{ x ≡ a 0 ( m o d n 0 ) x ≡ a 1 ( m o d n 1 ) . . . x ≡ a k ( m o d n k ) \left\{ \begin{aligned} x≡a_0(mod{\,}{\,}n_0) \\ x≡a_1(mod{\,}{\,}n_1) \\ ...{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}{\,}\\ x≡a_k(mod{\,}{\,}n_k) \end{aligned} \right. ⎩
⎨
⎧x≡a0(modn0)x≡a1(modn1)...x≡ak(modnk)
中国剩余定理的解法流程为:
- 计算所有模数的乘积 n = ∏ i = 0 k n i n = \prod_{i\ =\ 0}^{k}n_i n=∏i = 0kni
- 计算 m i = n / n i , c i = m i ∗ m i − 1 m_i = n / n_i, c_i = m_i * m_i^{-1} mi=n/ni,ci=mi∗mi−1
- 方程组的解为: x = ∑ i = 0 k a i c i ( m o d n ) x = \sum_{i\ =\ 0}^{k}{a_ic_i\ (mod\ n)} x=∑i = 0kaici (mod n)
2 Paillier算法原理
2.1 Paillier简介
在Paillier算法出现之前,基于公钥加密的算法主要有两个分支:
- 以RSA为代表的,基于大数因数分解难题的公钥加密算法
- 以ElGama为代表的,基于大数离散对数难题的公钥加密算法
Paillier加密算法,由Pascal Paillier于1999年发表,给出了公钥加密算法的一个新的分支领域。Paillier基于复合剩余类难题,满足加法同态和数乘同态,具有非常高效的运行时性能。
2.2 一个典型的应用场景

同态加密算法使得密文数据,在没有额外数据泄露的情况下,可以在第三方平台进行进一步加工处理。随着大规模云计算的兴起,尤其是涉及到敏感数据的云计算,同态加密算法将是其中至关重要的技术基础。我们以一个典型的联邦学习的例子为切入点,看看Paillier算法的原理和在实践中应用的问题。
假设Alice和Bob想共同训练一个网络模型,Alice和Bob各自持有一部分训练数据,并且他们不想把自己的数据泄露给对方。那么在训练期间,Alice和Bob需要交互各自训练的梯度数据,并根据双方的梯度数据,共同计算一个对双方都合适的梯度值,用来执行联合梯度下降过程。
2019年,Ligeng Zhu等人发表的“Deep Leakage from Gradients”论文中给出了一种算法[2],可以从几次迭代的梯度数据中,推断出训练的数据,标签,模型等一系列隐私信息。这使得在分布式机器学习中,通过传输梯度数据来进联合模型训练变得不再安全。那么如果在梯度数据传输的过程中,传输的是加密后的梯度数据,并且这些加密数据可以进行二次计算,那么便可以规避梯度数据传输过程带来的安全风险。
2.3 Paillier算法
2.3.1 密钥生成
类似于RSA算法,Paillier也拥有公钥和私钥对。
- Alice选择两个大素数p=11,q=19(目前已知512bit的非对称密钥已经可以破解,实际应用中通常选用非常大的素数)
- Alice计算p和q的乘积n = p * q = 209, 并计算λ = lcm(p – 1, q - 1)
- Alice选择一个随机整数g, g ∈ Z n 2 ∗ g\in {\mathbb Z}_{ {n^{ {2}}}}^{ {*}} g∈Zn2∗
- Alice定义函数 L ( x ) = x − 1 n L(x) = \frac{x-1}{n} L(x)=nx−1 , 并计算模反元素 μ = L ( g λ m o d n 2 ) − 1 m o d n μ = {L(g^\lambda\ mod\ n^2)}^{-1} mod{\,}{\,}n μ=L(gλ mod n2)−1modn
在上述过程中,Alice总计生成了6个数字:
p = 11
q = 19
n = 209
λ = 90
g = 147
μ = 153
Alice将 n 和g 封装成公钥 public-key = (n, g)
将λ和μ封装成私钥: private-key = (λ, μ)
2.3.2 加密
假设Bob需要加密明文m, 0 <= m < n. 且Bob收到了Alice发送过来的公钥(n, g)
- Bob选择一个随机数r,满足0 < r < n
- Bob计算加密后的密文 c = gm.rn mod n2
m = 8
r = 3
n_square = pow(n, 2) # n_square = 43681
c = gmpy2.mod(pow(g, m)*pow(r, n), n_square) # c = 32948
2.3.3 解密
假设c是Bob发送过来的密文,且 c ∈ Z n 2 ∗ c\in {\mathbb Z}_{
{n^{
{2}}}}^{
{*}} c∈Zn2∗
Alice计算明文 m = L ( c λ m o d n 2 ) ∗ μ m o d n m = L(c^\lambda\ mod\ n^2)*μ\ mod\ n m=L(cλ mod n2)∗μ mod n
c = 32948
m = gmpy2.mod(L(gmpy2.mod(pow(c, lam), n_square), n) * mu, n) # m = 8
正确性证明
为了证明解密操作的正确性,我们把加密的公式代入:
D E C ( c ) = L ( c λ m o d n 2 ) ∗ μ m o d n = L ( ( g m r n m o d n 2 ) λ m o d n 2 ) ∗ μ m o d n = L ( g λ m r λ n m o d n 2 ) ∗ μ m o d n DEC(c) = L(c^\lambda\ mod\ n^2) * μ mod n = L({
{(g}^mr^n\ mod\ n^2)}^\lambda\ mod\ n^2) * μ\ mod\ n = L{(g}^{\lambda m}r^{\lambda n}\ mod\ n^2) * μ\ mod\ n DEC(c)=L(cλ mod n2)∗μmodn=L((gmrn mod n2)λ mod n2)∗μ mod n=L(gλmrλn mod n2)∗μ mod n
根据卡米切尔定理(Carmichael’s function)有:
① r λ n ≡ 1 m o d n 2 \ \ r^{\lambda n} ≡1\ mod\ n^2 rλn≡1 mod n2
继续化简得:
D E C ( c ) = L ( g λ m m o d n 2 ) ∗ μ m o d n DEC(c) = L{(g}^{\lambda m}\ mod\ n^2) * μ\ mod\ n DEC(c)=L(gλm mod n2)∗μ mod n
由于 g ∈ Z n 2 ∗ , n + 1 ∈ Z n 2 ∗ g ∈ Z_{n^2}^\ast, n + 1 ∈ Z_{n^2}^\ast g∈Zn2∗,n+1∈Zn2∗, 那么一定存在唯一一对(a, b)使得:
② g λ m o d n 2 = ( 1 + n a λ ) ∗ b n λ m o d n 2 = 1 + a ∗ λ ∗ n m o d n 2 \ g^\lambda\ mod\ n^2 = {(1\ +\ n}^{a\lambda}) * b^{n\lambda}\ mod\ n^2 = 1 + a*λ*n\ mod\ n^2 gλ mod n2=(1 + naλ)∗bnλ mod n2=1+a∗λ∗n mod n2
把上述公式带入,高阶多项式按二项式定理展开,得:
D E C ( c ) = L ( ( ( 1 + n a λ ) b n λ ) m m o d n 2 ) ∗ μ m o d n = L ( 1 + a ∗ m ∗ λ ∗ n m o d n 2 ) ∗ μ m o d n DEC(c) = L({
{((1\ +\ n}^{a\lambda})b^{n\lambda})}^m\ mod\ n^2 ) * μ\ mod\ n = L(1 + a*m*λ*n\ mod\ n^2) * μ\ mod\ n DEC(c)=L(((1 + naλ)bnλ)m mod n2)∗μ mod n=L(1+a∗m∗λ∗n mod n2)∗μ mod n
这里我们再看下μ的取值,同样按照公式②展开,得
μ = L ( g λ m o d n 2 ) − 1 m o d n = L ( 1 + a ∗ λ ∗ n m o d n 2 ) − 1 m o d n μ = {L(g^\lambda\ mod\ n^2)}^{-1} mod n = {L(1 + a*λ*n\ mod\ n^2)}^{-1}\ mod\ n μ=L(gλ mod n2)−1modn=L(1+a∗λ∗n mod n2)−1 mod n
最后把函数L展开,得:
D E C ( c ) = ( a ∗ m ∗ λ m o d n 2 ) ∗ ( a ∗ λ m o d n 2 ) − 1 m o d n = m DEC(c) = (a*m*λ\ mod\ n^2) * {(a\ast\lambda\ mod\ n^2)}^{-1}\ mod\ n = m DEC(c)=(a∗m∗λ mod n2)∗(a∗λ mod n2)−1 mod n=m
2.3.4 同态加
假设Alice计算的梯度数据为m1, Bob计算的梯度数据为m2,Bob需要计算双方梯度数据的均值(m1 + m2)/ 2, 作为分布式梯度下降的梯度数据。
同态加的原理是利用了幂函数的 a x 1 ∗ a x 2 = a x 1 + x 1 a^{x1} * a^{x2} = a^{x1+x1} ax1∗ax2=ax1+x1的特性。对于Alice持有的数据m1的密文c1和Bob持有数据m2的密文c2,Bob使用如下公式计算同态加法运算:
c = c 1 ∗ c 2 m o d n 2 c = c1 * c2\ mod\ n^2 c=c1∗c2 mod n2
Alice使用私钥计算 D E C ( c ) = m 1 + m 2 DEC(c) = m1 + m2 DEC(c)=m1+m2
正确性证明
为了证明同态加的正确性, 我们把加密的公式代入同态加运算:
c = ( ( g m 1 r n m o d n 2 ) ∗ ( g m 2 r n m o d n 2 ) ) m o d n 2 = ( g m 1 r n g m 2 r n ) m o d n 2 = ( g m 1 + m 2 r 2 n ) m o d n 2 = E N C ( m 1 + m 2 ) c = ((g^{m1}r^n\ mod\ n^2) * (g^{m2}r^n\ mod\ n^2)) mod\ n^2 = (g^{m1}r^ng^{m2}r^n) mod\ n^2 = (g^{m1\ +m2}{r^2}^n) mod\ n^2 = ENC(m1 + m2) c=((gm1rn mod n2)∗(gm2rn mod n2))mod n2=(gm1rngm2rn)mod n2=(gm1 +m2r2n)mod n2=ENC(m1+m2)
解密c等价于:
D E C ( c ) = D E C ( E N C ( m 1 + m 2 ) ) = m 1 + m 2 DEC(c) = DEC(ENC(m1 + m2)) = m1 + m2 DEC(c)=DEC(ENC(m1+m2))=m1+m2
对于密文和明文相加的同态运算,我们当然可以先对明文加密,之后再对两个密文进行同态加运算的方式来计算。不过从上面的公式可以看出,扰动数据 r n r^n rn中的r是一个任意值。那么我们可以把计算密文c1和明文m2的和的计算转换为:
c 1 + m 2 = ( g m 1 ∗ r n m o d n 2 ∗ g m 2 m o d n 2 ) m o d n 2 = g m 1 + k ∗ r n m o d n 2 = E ( m 1 + m 2 ) c1 + m2 = (g^{m1}*r^n\ mod\ n^2 * g^{m2}\ mod\ n^2) mod\ n^2 = g^{m1}+k*r^n mod\ n^2 = E(m1+m2) c1+m2=(gm1∗rn mod n2∗gm2 mod n2)mod n2=gm1+k∗rnmod n2=E(m1+m2)
这样少了一次计算 r n r^n rn的运算量,提升了明文和密文相加运算的效率。
2.3.5 同态数乘
Paillier算法目前只支持明文和密文相乘的计算方式,不支持密文和密文相乘。
同态数乘的原理是利用了幂函数的axk = akx的特性。
Bob使用Alice对明文m1加密后的密文c1和明文k,计算
c = c 1 k m o d n 2 c = c1^k\ mod\ n^2 c=c1k mod n2
Alice使用私钥计算 D E C ( c ) = k ∗ m 1 DEC(c) = k*m1 DEC(c)=k∗m1
正确性证明
为了证明同态数乘的正确性, 我们把加密的公式代入同态数乘运算:
c = c 1 k m o d n 2 = ( g m 1 ∗ r n m o d n 2 ) k m o d n 2 = g k ∗ m 1 ∗ r 1 n m o d n 2 = E ( k ∗ m 1 ) c = c1^k\ mod\ n^2 = (g^{m1}*r^n\ mod\ n^2)^k\ mod\ n^2 = g^{k*m1}*r1^n\ mod\ n^2 = E(k*m1) c=c1k mod n2=(gm1∗rn mod n2)k mod n2=gk∗m1∗r1n mod n2=E(k∗m1)
解密c等价于:
D E C ( c ) = D E C ( E N C ( k ∗ m 1 ) ) = k ∗ m 1 DEC(c) = DEC(ENC(k * m1)) = k * m1 DEC(c)=DEC(ENC(k∗m1))=k∗m1
2.4 算法优化
2.4.1 参数g优化
在原始Paillier方案中,g的取值只需满足 g ∈ Z n 2 ∗ g∈\mathbb{Z}_{n^2}^\ast g∈Zn2∗。Ivan和Mads在论文中给出了使用g = n + 1 的优化方案[3],并且证明了使用此方案后,可以和原始Paillier算法保持相同的安全性。
在使用g = n + 1后,实现密钥生成和加密过程的性能提升。
密钥生成:
把g = n + 1带入μ的生成公式,得
μ = L ( g λ m o d n 2 ) − 1 m o d n = L ( ( n + 1 ) λ m o d n 2 ) − 1 m o d n = L ( ( 1 + λ n ) m o d n 2 ) − 1 m o d n = λ − 1 m o d n μ = {L(g^\lambda\ mod\ n^2)}^{-1}\ mod\ n = {L({(n\ +\ 1)}^\lambda\ mod\ n^2)}^{-1}\ mod\ n = {L((1\ +\ \lambda n)\ mod\ n^2)}^{-1}\ mod\ n = \lambda^{-1}\ mod\ n μ=L(gλ mod n2)−1 mod n=L((n + 1)λ mod n2)−1 mod n=L((1 + λn) mod n2)−1 mod n=λ−1 mod n
μ 生成可以直接取λ 对 n的模反元素。
加密:
把g = n+1,带入加密公式,得 c = g m r n m o d n 2 = ( n + 1 ) m r n m o d n 2 = ( n ∗ m + 1 ) ∗ r n m o d n 2 c = g^mr^n\ mod\ n^2 = {(n\ +\ 1)}^mr^n\ mod\ n^2 = (n * m + 1) * r^n\ mod\ n^2 c=gmrn mod n2=(n + 1)mrn mod n2=(n∗m+1)∗rn mod n2
加密过程把计算g的m次幂的操作,变成了简单的乘法操作:
c = (n*m+1)*rn mod n2
2.4.2 高阶幂运算优化
在优化了原始Paillier加密过程的 g m g^m gm幂运算后,加密操作中最耗性能的操作就是对 r n r^n rn高阶幂函数的计算。2010年,Ivan Damg˚ard, Mads Jurik 和 Jesper Buus Nielsen给出了优化 r n r^n rn这个高阶幂函数计算的方案[5],并证明了使用此方案后,可以和原始Paillier算法保持相同的安全性。
密钥生成:
要求p≡q≡3 (mod 4), 且gcd(p – 1, q – 1) = 2.
λ = (p - 1)(q - 1) / 2
选择一个随机数x,且 x ∈ Z n ∗ , h = − x 2 m o d n x ∈Z_n^\ast, h = -x^2\ mod\ n x∈Zn∗,h=−x2 mod n。
选择一个自然数s,对于原版Paillier, 相当于为s设定了s = 1
h s = h n s m o d n s + 1 h_s = h^{n^s} mod\ n^{s\ +\ 1} hs=hnsmod ns + 1
优化后,新的公钥为public-key=(n, hs)
加密:
生成一个随机数α, a ∈ Z 2 ⌈ k / 2 ⌉ a ∈Z_{2^{\lceil k\ /\ 2\rceil}} a∈Z2⌈k / 2⌉, 其中k是密钥长度
优化后使用如下公式进行加密操作:
c = ( n ∗ m + 1 ) h s α m o d n s + 1 c = (n\ \ast\ m\ +\ 1){h_s}^\alpha\ mod\ n^{s\ +\ 1} c=(n ∗ m + 1)hsα mod ns + 1
因为取值α << n, 使得加密计算过程中,计算 h s α {h_s}^\alpha hsα的性能,优于计算 r n r^n rn的性能.
2.4.3 使用中国剩余定理
使用中国剩余定理,可以把诸如 a x m o d n a^x\ mod\ n ax mod n形式的高阶幂函数取模操作,分解为低阶幂函数对n的因子取模的操作。
由于分解操作,需要使用到生成私钥的关键数据p和q,所以使用中国剩余定理对高阶幂函数取模操作的优化,只能应用在使用私钥的解密操作中。
解密:
使用中国剩余定理优化解密算法的步骤如下:
- 定义分解因子p和q对应的函数 L p ( x ) = x − 1 p , L q ( x ) = x − 1 q L_p(x) = \frac{x - 1}{p} , L_q(x) = \frac{x - 1}{q} Lp(x)=px−1,Lq(x)=qx−1
- 计算 h p ≡ ( p − 1 ) ∗ q ( m o d p ) , h q ≡ ( q − 1 ) ∗ p ( m o d q ) h_p ≡ (p - 1) * q (mod\ p), h_q ≡ (q - 1) * p (mod\ q) hp≡(p−1)∗q(mod p),hq≡(q−1)∗p(mod q)
- 计算 m p = L p ( c p − 1 m o d p 2 ) h p m o d p , m q = L q ( c q − 1 m o d q 2 ) h q m o d q m_p = L_p(c^{p\ -\ 1}\ mod\ p^2)\ h_p\ mod\ p,\ m_q = L_q(c^{q\ -\ 1}\ mod\ q^2)\ h_q\ mod\ q mp=Lp(cp − 1 mod p2) hp mod p, mq=Lq(cq − 1 mod q2) hq mod q
- 计算m = CRT(m_p, m_q) mod n, m 即为使用中国剩余定理优化的解密后的明文
2.4.4 性能优化对比
算法使用Python代码实现,密钥长度取2048bit, s参数取1,取模之前的幂运算均采用模幂方法优化。其中后面的优化均是在前面优化的基础上进行的优化。
| 原版 | 参数g优化 | 幂运算优化(s=1) | 中国剩余定理(s =1) | |
|---|---|---|---|---|
| 密钥生成 | 98.412 | 77.913 | 169.511 | 169.812 |
| 加密 | 20.043 | 9.107 | 4.704 | 4.704 |
| 解密 | 11.692 | 8.859 | 8.859 | 2.705 |
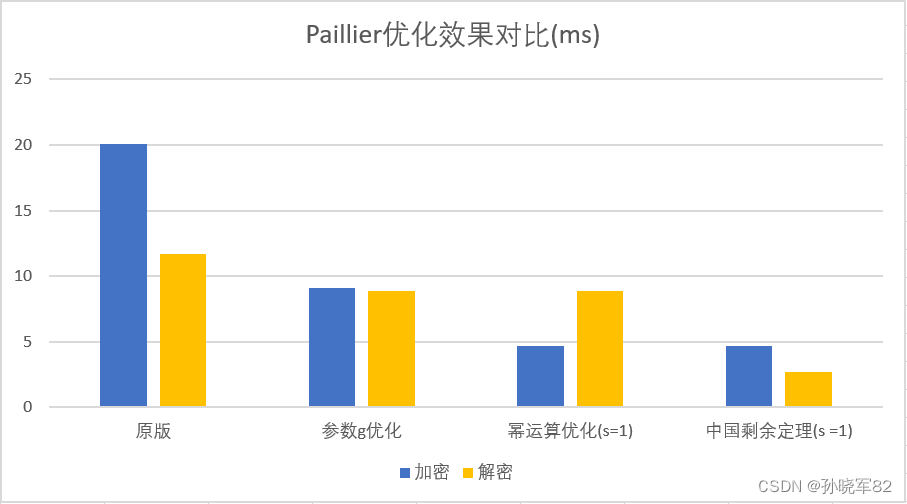
从表1和图2中可以看到,经过参数g优化和幂运算优化后,加密运算的效率较之原版方案提升了约3.26倍。经过使用中国剩余定理优化后,解密运算的效率较之原版方案提升了约3.32倍。在密钥生成上,使用了幂运算优化后,密钥生成的时间增加了约42%。考虑到密钥生成运算的次数,通常远小于加解密运算的次数,相比之下密钥生成的性能损失通常可以忽略不计。
2.5 来自多方计算的安全问题
在上面Alice和Bob使用Paillier同态加密来进行分布式梯度值计算时,Alice持有私钥,对Bob加密后的梯度数据,进行同态运算,并生成最终分布式梯度计算的梯度值。这里有一个问题,在这个场景下,虽然Alice没有获得Bob的直接或加密后的梯度数据,但Alice知道最终的梯度值,这使得Alice可以根据差分结果,猜测出Bob本次计算的梯度数据,从而产生安全问题。
在多方安全计算中,由于同态计算的算法,不一定能够提供安全保证,使得我们必须应对计算过程中可能出现的安全问题。对于Alice和Bob的计算分布式梯度值的场景,可以根据当前的学习率引入合适的扰动数据来规避差分隐私问题,或者参与计算的多方至少是三方。
3 功能扩展
在原版Paillier中,明文m的定义域是[0, n)。在Alice和Bob的进行的分布式机器学习场景中,需要能够对浮点和负数进行加密运算。在实际应用中,如果只能加密正整数,那么Paillier的应用场景会受到较大的限制。实际上,计算机的布尔电路只能对0和1的二进制数据进行计算,无论是浮点数还是负数,甚至是整数的计算,都是通过特定的计算规则来完成的,我们可以参照这些规则,实现Paiiler算法对浮点数和负数的支持。
3.1 浮点数支持

IEEE 754标准中,单精度浮点表示采用1位符号,8位阶码和23位分数。
对于浮点数,我们可以将所有参与计算的数值,编码为更小的单位,在计算完成后再解码。比如浮点数3.14,可以预先乘以100, 即3.14 = 314 * {10}^{-2}。之后计算过程中,整数部分和指数部分分别运算。
在计算机中,浮点数以符号位(Sign),阶码(Exponent)和分数(Fraction)三部分联合来标识,底数(Base)固定为2。我们仍旧以3.14为例, 3.14 = 0.785 ∗ 2 2 = [ 11.0010001 ] 2 3.14 = 0.785 * 2^2 = [11.0010001]_2 3.14=0.785∗22=[11.0010001]2。实际使用中,为了表示更大的范围,分数部分的取值范围要求 1 <= fraction < 2, 这样保证了分数部分的首位总是为1,这样小数部分可以隐藏首位的1。为了使阶码可以使用负数,浮点标准规定了指数部分使用一个偏移值(Bias),这样浮点数的值的计算方式为:
x = − 1 s i g n ∗ ( 1 + F r a c t i o n ) ∗ 2 ( E x p o n e n t − B i a s ) x = {-1}^{sign} * (1 + Fraction) * 2^{(Exponent\ -\ Bias)} x=−1sign∗(1+Fraction)∗2(Exponent − Bias)
在扩充Paillier算法定义域到浮点数时,浮点数各个部分的计算,均需程序来实现。这里我们参照浮点数的表示法,且不使用隐藏位,假设给定Bias=8,那么3.14就可以编码为(E = 2,F=200(0.785 * 28))。我们再把整数2,经过同样的编码,得到(E=2, F=128)
在Paillier计算中,由于阶码相同,3.14 + 2 = (E = 2, F = 328)。最终执行解码,得到 328 ∗ 2 − 8 ∗ 2 2 = 5.125 328 * 2^{-8} * 2^2 = 5.125 328∗2−8∗22=5.125。计算结果存在较大的精度损失,实际应用中,我们可以通过增大Bias的值,来提升计算结果的精度。
对于同态数乘来说,由于不需要阶码对齐,那么只需对F值做数乘,即可得到正确的结果。同样对于3.14, 乘以3后得到(E = 2, F = 600),之后解码,得到 600 ∗ 2 − 8 ∗ 2 2 = 9.375 600 * 2^{-8} * 2^2 = 9.375 600∗2−8∗22=9.375。同样由于示例中Bias取值问题,计算结果出现了较大的误差。
3.2 负数支持
在计算机中,负数是以补码的方式标识的。整数和负数相加,是通过溢出来使得计算结果符合预期值,如果我们把负数的字节扩充,那么会得到一个原有字节空间的最大值和对应负数之和的正数,在此基础上使用此正数进行四则运算,之后再缩容到原来的字节空间,那么得到的仍旧是正确的结果。
类似的,为了使Paillier能够支持负数的计算,我们可以给负数m_1增加一个周期值n, 来把负数m_1转换为正整数。那么对于同态加运算来说,计算结果c=ENC(m_1 + m_2 + n)。
此时同态加计算的结果为:
- 当 m 1 + m 2 > = 0 m_1 + m_2 >= 0 m1+m2>=0时, D E C ( c ) = m 1 + m 2 DEC(c) = m_1 + m_2 DEC(c)=m1+m2
- 当 − n < = m 1 + m 2 < 0 -n <= m_1 + m_2 < 0 −n<=m1+m2<0时, D E C ( c ) = m 1 + m 2 + n DEC(c) = m_1 + m_2 + n DEC(c)=m1+m2+n
- 当 m 1 + m 2 < − n m_1 + m_2 < -n m1+m2<−n 时,计算结果不正确
同态数乘的计算结果为:
- 当 k ∗ m 1 > = 0 k*m_1 >= 0 k∗m1>=0 , 时 D E C ( c ) = k ∗ m 1 DEC(c) = k*m_1 DEC(c)=k∗m1
- 当 − n < = k ∗ m 1 < 0 -n <= k*m_1 < 0 −n<=k∗m1<0时, D E C ( c ) = k ∗ m 1 + n DEC(c) = k*m_1 + n DEC(c)=k∗m1+n
- 当 k ∗ m 1 < − n k*m_1 < -n k∗m1<−n时,计算结果不正确
为了统一以上出现的各种场景,我们可以做如下限定:
- 操作数在参与同态计算前对n取模,用来统一正数可以直接参与计算,负数则需要补n再进行计算的问题。
- 设定操作数的最大值MAX_VALUE,比如32位整型的最大值。并使得n的取值大于3 * MAX_VALUE,这样使得对于合法的 m 1 和 m 2 m_1和m_2 m1和m2,不存在 m 1 + m 2 < − n m_1 + m_2 < -n m1+m2<−n的场景,且 m 1 + m 2 < 0 m_1 + m_2 < 0 m1+m2<0时,计算结果总是大于MAX_VALUE。
至此,我们可以使用统一的规则,来处理负数参与同态运算时的各种场景。
4 主要公钥加密算法对比
Paillier,RSA和ELGamal算法均为典型的基于公钥的加密算法,我们从功能指标和性能指标两个方向,来对比这些加密算法的区别和联系。
4.1 功能指标对比
| Paillier | RSA | ELGamal | |
|---|---|---|---|
| 安全基础 | 复合剩余类问题 | 大数分解问题 | 离散对数问题 |
| 语义安全 | 是 | 否(可以使用诸如OAEP的随机填充算法来达到语义安全的效果) | 是 |
| 公钥加密/私钥解密 | 支持 | 支持 | 支持 |
| 私钥签名/公钥验签 | 不支持(可以实现更为复杂的门限签名) | 支持 | 支持 |
| 算法复杂程度(非时间复杂度) | 高 | 低 | 中 |
| 同态计算 | 同态加,同态数乘 | 同态乘 | 同态乘 |
4.2 性能指标对比
对4096-bit大小的明文进行加密:
| Paillier | RSA | ELGamal | ||||
|---|---|---|---|---|---|---|
| s=1 | s=2 | s=3 | s=4 | |||
| 密钥长度 | 4096 | 2048 | 1366 | 1024 | 4096 | 4096 |
| 密文大小 | 8192 | 6144 | 5462 | 5120 | 4096 | 8192 |
| 膨胀系数 | 2 | 1.5 | 1.33 | 1.25 | 1 | 2 |
对1-bit大小的数据进行加密和解密运算,统计数据单位为ms。
| Paillier | RSA | ELGamal | |||
|---|---|---|---|---|---|
| s=1 | s=2 | s=4 | |||
| 加密 | |||||
| 1024 | 0.262 | 0.284 | 0.387 | 0.002 | 0.264 |
| 2048 | 0.955 | 1.067 | 1.480 | 0.004 | 0.967 |
| 4096 | 3.705 | 4.146 | 5.755 | 0.008 | 3.711 |
| 8192 | 14.507 | 16.244 | 22.617 | 0.015 | 14.467 |
| 解密 | |||||
| 1024 | 0.149 | 0.153 | 0.214 | 0.039 | 0.132 |
| 2048 | 0.503 | 0.559 | 0.780 | 0.132 | 0.489 |
| 4096 | 1.898 | 2.128 | 2.958 | 0.486 | 1.865 |
| 8192 | 7.349 | 8.244 | 11.461 | 1.854 | 7.286 |
5 同态加密的应用
同态加密使得云计算和人工智能时代的数据,算法,算力可以解耦,对于一家企业来说,无需完整具备以上三个条件也可以在云计算和人工智能时代获取一席之地。
我们可以假设这样一个场景,协和医院拥有大量的高价值医疗行业数据,并想通过京东云服务的云计算和人工智能来进行数据分析。在同态加密之前,能够采取的方案要么时协和将隐私数据的明文提供给京东云计算来进行数据分析,使得隐私数据外泄;要么是京东为持有敏感数据的企业,采用传统的On-Premise模式,放弃云计算带来的各种便利。而同态加密,使得协和可以以安全的方式向京东云服务提供隐私数据,京东云计算也可以在不解密的情况下使用这些数据进行数据分析,从而解决了这个两难问题。依靠同态加密,使得基于数理统计相关的算法和数据可以独立开来,既可以依托于云计算的算法和算力,又完美地保护了客户的隐私数据。
同态加密的应用不止限于简单的数据分析,在以下很多场景下都有其用武之地:
隐私集合求交
在隐私集合求交中,其中一个参与方构建如下的多项式
d i = r i ∏ x ∈ X ( c i − x ) d_i = r_i\prod_{x\in X}{(c_i-x)} di=ri∏x∈X(ci−x)
其中r_i为随机数, c i c_i ci是另一参与方提供的求交数据的同态加密之后的密文,x是己方持有的求交数据同态加密后的密文。如果 c i c_i ci 和x中任一数据相同,那么得到的 d i d_i di,在解密后的值为0,否则不为0。
联邦学习
在联邦学习过程中,联邦学习的参与者之间使用同态加密传递学习过程中的中间信息,从而避免信息接收方推断出其它参与联邦学习的参与方的私密信息,保证了联邦学习过程中的信息安全性。
门限签名
门限签名是秘密共享和数字签名技术的一种结合。传统的签名技术,私钥被保存在一个可信的中心节点中。(t, n)门限签名方案,把秘密分发给n个成员,组成一个签名群体。在这个群体中,单个成员不再具有签名的权限,只有集齐了t个或更多诚实的成员,才能对数据进行数字签名,这个的t即是门限值。门限签名防止了单个中心节点导致的秘密泄露或职权滥用,在证书颁发,多方身份识别,资产托管,电子投票等诸多领域具有应用价值。
联合风控
在银行或金融机构进行风险评估时,需要大量关于企业和个人的隐私信息。对于参与联合风控的数据提供方来说,不希望自身的隐私数据暴露给银行或金融机构,而银行和金融机构也不希望风控规则在三方环境下执行。参与联合风控的数据提供方,通过对自身数据进行同态加密,使得银行或金融机构能够正常进行风险评估,同时又不泄露数据提供方的数据信息。
同态加密技术被誉为隐私计算技术“皇冠上的明珠”,这项技术使得我们在不需要信赖云服务提供商的前提下,使用云服务提供商的计算和存储能力,从而解决了云计算中的隐私数据保护问题。同态加密技术的特点,使其在数字货币,金融应用,医疗保健等领域有着非常广泛的应用场景和实践价值。同态加密技术为云计算和云存储在应对隐私数据时,提供了一种可靠的解决方案。对同态加密技术的关注和研究,使得企业具有更多的理论和方案,来应对和解决私密信息的计算和存储问题,为数据的全面互联互通,提供了一种行之有效的解决方案。
配套源代码
https://github.com/sunxiaojun/privacy-preserving-computing
参考文献
[1] P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Proceedings of Advances in Cryptology (EUROCRYPT’99),pp. 223–238, Prague, Czech Republic, May 1999.
[2] Zhu, L., Liu, Z., Han, S.: Deep leakage from gradients. In: Annual Conference on Neural Information Processing Systems (NeurIPS) (2019)
[3] D. Choi, S. Choi, and D. Won, “Paillier’s cryptosystem revisited,” in Proceedings of the 8th ACM Conference on Computer and Communications Security(CCS’01), pp. 206–214, Philadelphia, Pennsylvania, USA, Nov. 2001
[4] I. Damgard and M. Jurik. A generalization, of Paillier’s Eurocrypt '99, volume 1592 of LNCS. IACR,Springer-Verlag, 1999.
[5] I. Damg˚ard, J. Jurik, and J. Nielsen, “A generalization of paillier’s public-key system with applications to electronic voting,” International Journal of Information Security, no. 9, pp. 371–385, 2010.
[6] Cao, Z. and Liu, L., “The Paillier’s Cryptosystem and Some Variants Revisited.” arXiv preprint arXiv:1511.05787,2015.