目录
简答题
1、什么是算法?算法有哪些特征?
算法是求解问题的一系列计算步骤。算法具有有限性、确定性、可行性、输入性和输出性。
2、什么是直接递归和间接递归?消除递归一般要用什么数据结构?
直接递归:一个 f 函数定义中直接调用 f 函数自己。
间接递归:一个 f 函数定义中调用 g 函数,而 g 函数的定义中调用 f 函数。消除递归一般要用栈实现。
3、分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题,分别解决子问题,最后将子问题的解组合起来形成原问题的解。这要求原问题和子问题:
问题规模不同,问题性质相同。
4、在寻找 n 个元素中第 k 小元素问题中,如快速排序算法思想,运用分治算法对 n个元素进行划分,如何选择划分基准?
随机选择一个元素作为划分基准、取子序列的第一个元素作为划分基准、用中位数的中位数方法寻找划分基准。
5、快速排序算法是根据分治策略来设计的,简述其基本思想。
对于无序序列 a[low..high]进行快速排序,整个排序为“大问题”。选择其中的一个基准 base=a[i](通常以序列中第一个元素为基准),将所有小于等于 base 的元素移动到它的前面,所有大于等于 base 的元素移动到它的后面,即将基准归位到 a[i],这样产生a[low..i-1]和 a[i+1..high]两个无序序列,它们的排序为“小问题”。当 a[low..high]序列只有一个元素或者为空时对应递归出口。
所以快速排序算法就是采用分治策略,将一个“大问题”分解为两个“小问题”来求解。由于元素都是在 a 数组中,其合并过程是自然产生的,不需要特别设计。
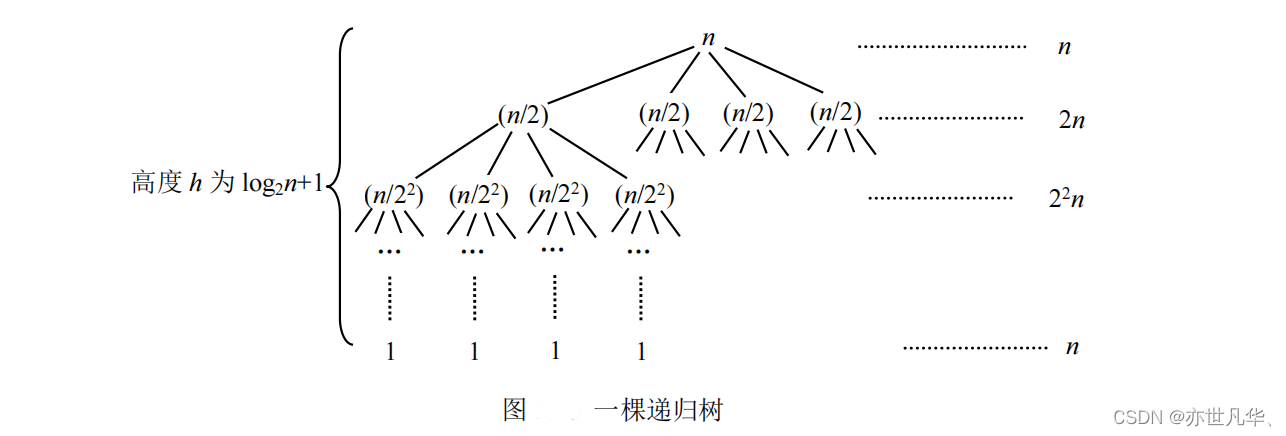
6、假设含有 n 个元素的待排序的数据 a 恰好是递减排列的,说明调用 QuickSort(a,0,n-1)递增排序的时间复杂度为 O(
)。
此时快速排序对应的递归树高度为 O(n),每一次划分对应的时间为 O(n),以整个排序时间为 O()。
7、哪些算法采用分治策略。
其中二路归并排序和折半查找算法采用分治策略。
8、适合并行计算的问题通常表现出哪些特征?
1)将工作分离成离散部分,有助于同时解决。例如,对于分治法设计的串行算法,可以将各个独立的子问题并行求解,最后合并成整个问题的解,从而转化为并行算法。
2)随时并及时地执行多个程序指令。
3)多计算资源下解决问题的耗时要少于单个计算资源下的耗时。
9、设有两个复数 x=a+bi 和 y=c+di。复数乘积 xy 可以使用 4 次乘法来完成,即xy=(ac-bd)+(ad+bc)i。设计一个仅用 3 次乘法来计算乘积 xy 的方法。
xy=(ac-bd)+((a+b)(c+d)-ac-bd)i。由此可见,这样计算 xy 只需要 3 次乘法(即ac、bd 和(a+b)(c+d)乘法运算)。
10、 有 4 个数组 a、b、c 和 d,都已经排好序,说明找出这 4 个数组的交集的方法。
采用基本的二路归并思路,先求出 a、b 的交集 ab,再求出 c、d 的交集 cd,最后求出 ab 和 cd 的交集,即为最后的结果。也可以直接采用 4 路归并方法求解。
11、简要比较蛮力法和分治法。
蛮力法是一种简单直接地解决问题的方法,适用范围广,是能解决几乎所有问题的一般性方法,常用于一些非常基本、但又十分重要的算法(排序、查找、矩阵乘法和字符串匹配等),蛮力法主要解决一些规模小或价值低的问题,可以作为同样问题的更高效算法的一个标准。而分治法采用分而治之思路,把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题直到问题解决。分治法在求解问题时,通常性能比蛮力法好。
12、在采用蛮力法求解时什么情况下使用递归?
如果用蛮力法求解的问题可以分解为若干个规模较小的相似子问题,此时可以采用递归来实现算法
13、回溯法在问题的解空间树中,按什么策略,从根结点出发搜索解空间树?
深度优先
14、对于回溯法说法错误的是
回溯算法需要借助队列这种结构来保存从根结点到当前扩展结点的路径
15、回溯法的效率依赖于哪些因素?
满足显约束的值的个数、计算约束函数的时间、计算限界函数的时间
16、什么函数是回溯法中为避免无效搜索采取的策略?
剪枝函数
17、回溯法的搜索特点是什么?
回溯法在解空间树中采用深度优先遍历方式进行解搜索,即用约束条件和限界函数考察解向量元素 x[i]的取值,如果 x[i]是合理的就搜索 x[i]为根结点的子树,如果x[i]取完了所有的值,便回溯到 x[i-1]。
18、用回溯法解 0/1 背包问题时,该问题的解空间是何种结构?用回溯法解流水作业调
度问题时,该问题的解空间是何种结构?
用回溯法解 0/1 背包问题时,该问题的解空间是子集树结构。用回溯法解流水作业调度问题时,该问题的解空间是排列树结构。
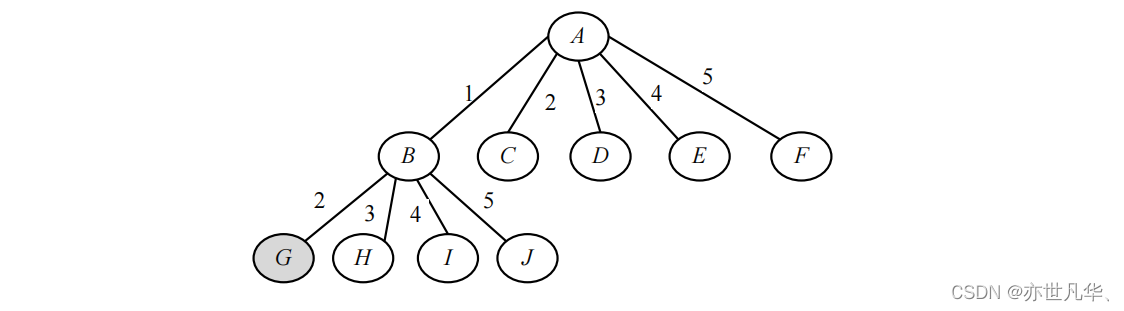
19、对于递增序列 a[]={1,2,3,4,5},采用回溯法求全排列,以 1、2 开头的排列一定最先出现吗?为什么?
是的。对应的解空间是一棵排列树,如图所示给出前面 3 层部分,显然最先产生的排列是从 G 结点扩展出来的叶子结点,它们就是以 1、2 开头的排列。
20、考虑 n 皇后问题,其解空间树为由 1、2、…、n 构成的 n!种排列所组成。现用回溯法求解,如下:
(1)通过解搜索空间说明 n=3 时是无解的。
n=3 时的解搜索空间如图所示,不能得到任何叶子结点,所有无解。
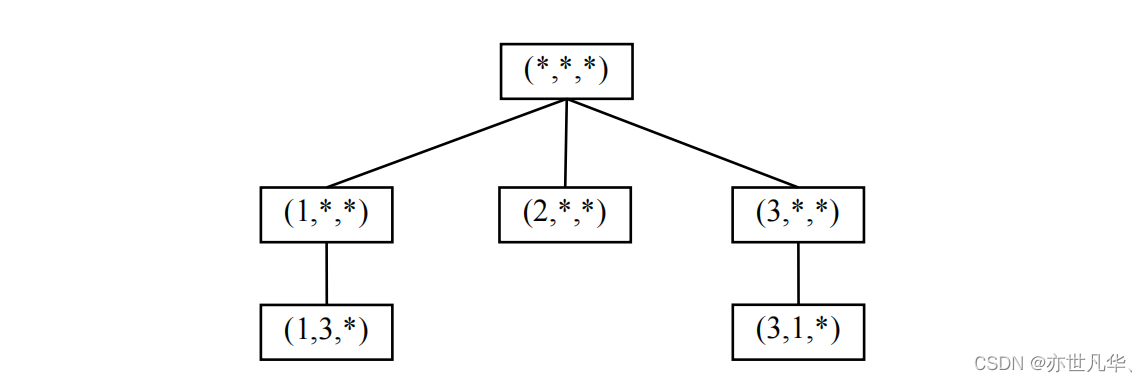
(2)给出剪枝操作。
剪枝操作是任何两个皇后不能同行、同列和同两条对角线。
(3)最坏情况下在解空间树上会生成多少个结点?分析算法的时间复杂度。
最坏情况下每个结点扩展 n 个结点,共有个结点,算法的时间复杂度为O(
)
21、分枝限界法在问题的解空间树中,按什么策略,从根结点出发搜索解空间树。
广度优先
22、常见的两种分枝限界法为:
队列式(FIFO)分枝限界法与优先队列式分枝限界法。
23、分枝限界法求解 0/1 背包问题时,活结点表的组织形式是
大根堆
24、采用最大效益优先搜索方式的算法是
分枝限界法
25、优先队列式分枝限界法选取扩展结点的原则是
结点的优先级
26、简述分枝限界法的搜索策略。
分枝限界法的搜索策略是广度优先遍历,通过限界函数可以快速找到一个解或者最优解。
27、有一个 0/1 背包问题,其中 n=4,物品重量为(4,7,5,3),物品价值为(40,42,25,12),背包最大载重量 W=10,给出采用优先队列式分枝限界法求最优解的过程。
求解过程如下:
1)根结点 1 进队,对应结点值:e.i=0,e.w=0,e.v=0,e.ub=76,x:[0,0,0,0]。
2)出队结点 1:左孩子结点 2 进队,对应结点值:e.no=2,e.i=1,e.w=4,e.v=40,e.ub=76,x:[1,0,0,0];右孩子结点 3 进队,对应结点值:e.no=3,e.i=1,
e.w=0,e.v=0,e.ub=57,x:[0,0,0,0]。
3)出队结点 2:左孩子超重;右孩子结点 4 进队,对应结点值:e.no=4,e.i=2,e.w=4,e.v=40,e.ub=69,x:[1,0,0,0]。
4)出队结点 4:左孩子结点 5 进队,对应结点值:e.no=5,e.i=3,e.w=9,e.v=65,e.ub=69,x:[1,0,1,0];右孩子结点 6 进队,对应结点值:e.no=6,e.i=3,e.w=4,e.v=40,e.ub=52,x:[1,0,0,0]。
5)出队结点 5:产生一个解,maxv= 65,bestx:[1,0,1,0]。
6)出队结点 3:左孩子结点 8 进队,对应结点值:e.no=8,e.i=2,e.w=7,e.v=42,e.ub=57,x:[0,1,0,0];右孩子结点 9 被剪枝。
7)出队结点 8:左孩子超重;右孩子结点 10 被剪枝。
8)出队结点 6:左孩子结点 11 超重;右孩子结点 12 被剪枝。
9)队列空,算法结束,产生的最优解:maxv= 65,bestx:[1,0,1,0]。
28、有一个流水作业调度问题,n=4,a[]={5,10,9,7},b[]={7,5,9,8},给出采用优先队列式分枝限界法求一个解的过程。
求解过程如下:
1)根结点 1 进队,对应结点值:e.i=0,e.f1=0,e.f2=0,e.lb=29, x:[0,0,0,0]。
2)出队结点 1:扩展结点如下:
进队(j=1):结点 2,e.i=1,e.f1=5,e.f2=12,e.lb=27,x:[1,0,0,0]。
进队(j=2):结点 3,e.i=1,e.f1=10,e.f2=15,e.lb=34,x:[2,0,0,0]。
进队(j=3):结点 4,e.i=1,e.f1=9,e.f2=18,e.lb=29,x:[3,0,0,0]。
进队(j=4):结点 5,e.i=1,e.f1=7,e.f2=15,e.lb=28,x:[4,0,0,0]。
3)出队结点 2:扩展结点如下:
进队(j=2):结点 6,e.i=2,e.f1=15,e.f2=20,e.lb=32,x:[1,2,0,0]。
进队(j=3):结点 7,e.i=2,e.f1=14,e.f2=23,e.lb=27,x:[1,3,0,0]。
进队(j=4):结点 8,e.i=2,e.f1=12,e.f2=20,e.lb=26,x:[1,4,0,0]。
4)出队结点 8:扩展结点如下:
进队(j=2):结点 9,e.i=3,e.f1=22,e.f2=27,e.lb=31,x:[1,4,2,0]。
进队(j=3):结点 10,e.i=3,e.f1=21,e.f2=30,e.lb=26,x:[1,4,3,0]。
5)出队结点 10,扩展一个 j=2 的子结点,有 e.i=4,到达叶子结点,产生的一个解
是 e.f1=31,e.f2=36,e.lb=31,x=[1,4,3,2]。
该解对应的调度方案是:第 1 步执行作业 1,第 2 步执行作业 4,第 3 步执行作业
3,第 4 步执行作业 2,总时间=36。
29、贪心算法的基本要素的是
贪心选择性质
30、什么问题不能使用贪心法解决。
n 皇后问题
31、采用贪心算法的最优装载问题的主要计算量在于将集装箱依其重量从小到大排序,故算法的时间复杂度为
O(nlog2n)
32、关于 0/ 1 背包问题
对于同一背包与相同的物品,做背包问题取得的总价值一定大于等于做 0/1 背包问题。
33、一棵哈夫曼树共有 215 个结点,对其进行哈夫曼编码,共能得到( )个不同的码字。
108
34、求解哈夫曼编码中如何体现贪心思路?
在构造哈夫曼树时每次都是将两棵根结点最小的树合并,从而体现贪心的思路。
35、举反例证明 0/1 背包问题若使用的算法是按照 vi/wi的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解(此题说明 0/1 背包问题与背包问题的不同)。
例如,n=3,w={3,2,2},v={7,4,4},W=4 时,由于 7/3 最大,若按题目要求的方法,只能取第一个,收益是 7。而此实例的最大的收益应该是 8,取第 2、3个物品。
36、通常以自底向上的方式求解最优解的是
动态规划法
37、备忘录方法是什么算法的变形。
动态规划法
38、动态规划算法基本要素的是。
子问题重叠性质
39、一个问题可用动态规划算法或贪心算法求解的关键特征是问题的:
最优子结构性质
40、简述动态规划法的基本思路。
动态规划法的基本思路是将待求解问题分解成若干个子问题,先求子问题的解,然后从这些子问题的解得到原问题的解。
41、简述动态规划法与贪心法的异同。
动态规划法的 3 个基本要素是最优子结构性质、无后效性和重叠子问题性质,而贪心法的两个基本要素是贪心选择性质和最优子结构性质。所以两者的共同点是都要求问题具有最优子结构性质。
两者的不同点如下:
(1)求解方式不同,动态规划法是自底向上的,有些具有最优子结构性质的问题只能用动态规划法,有些可用贪心法。而贪心法是自顶向下的。
(2)对子问题的依赖不同,动态规划法依赖于各子问题的解,所以应使各子问题最优,才能保证整体最优;而贪心法依赖于过去所作过的选择,但决不依赖于将来的选择,也不依赖于子问题的解。
42、简述动态规划法与分治法的异同。
两者的共同点:
是将待求解的问题分解成若干子问题,先求解子问题,然后再从这些子问题的解得到原问题的解。
两者的不同点是:
适合于用动态规划法求解的问题,分解得到的各子问题往往不是相互独立的(重叠子问题性质),而分治法中子问题相互独立;另外动态规划法用表保存已求解过的子问题的解,再次碰到同样的子问题时不必重新求解,而只需查询答案,故可获得多项式级时间复杂度,效率较高,而分治法中对于每次出现的子问题均求解,导致同样的子问题被反复求解,故产生指数增长的时间复杂度,效率较低
43、哪些属于动态规划算法?
判断算法是否具有最优子结构性质、无后效性和重叠子问题性质。直接插入排序算法、简单选择排序算法 和 二路归并排序算法 均属于动态规划算法。
计算题
时间复杂度的计算
一、


二、

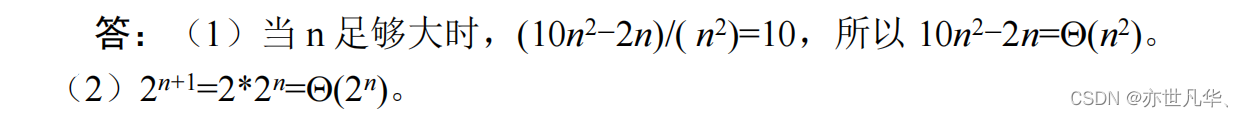
三、
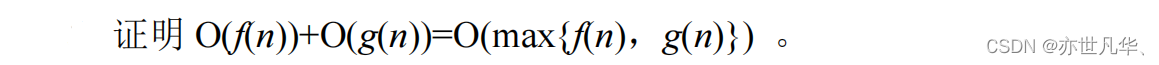

递归算法计算
一、


二、


三、


四、



五、


六、


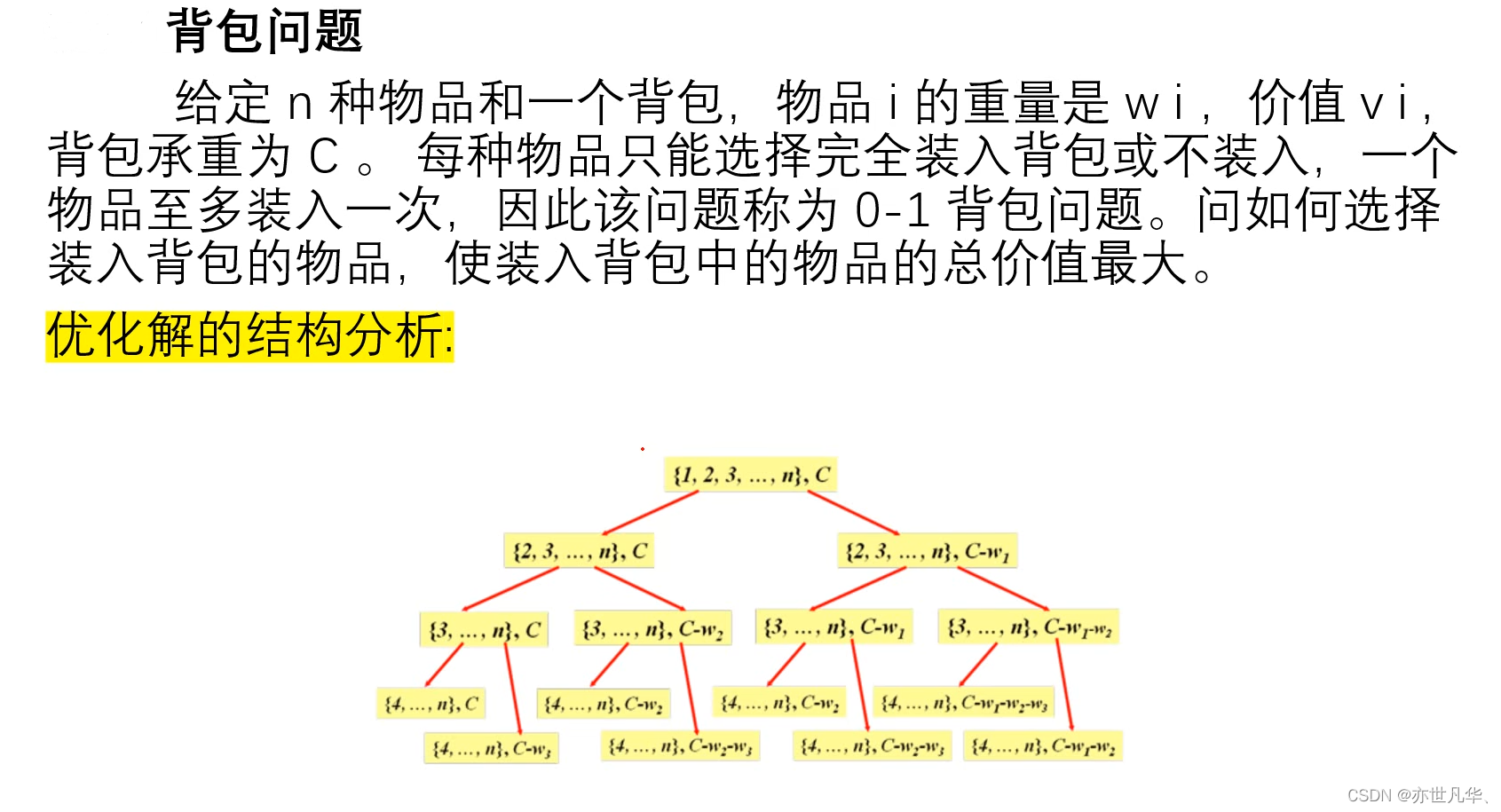
背包问题(0-1背包问题)


回溯法

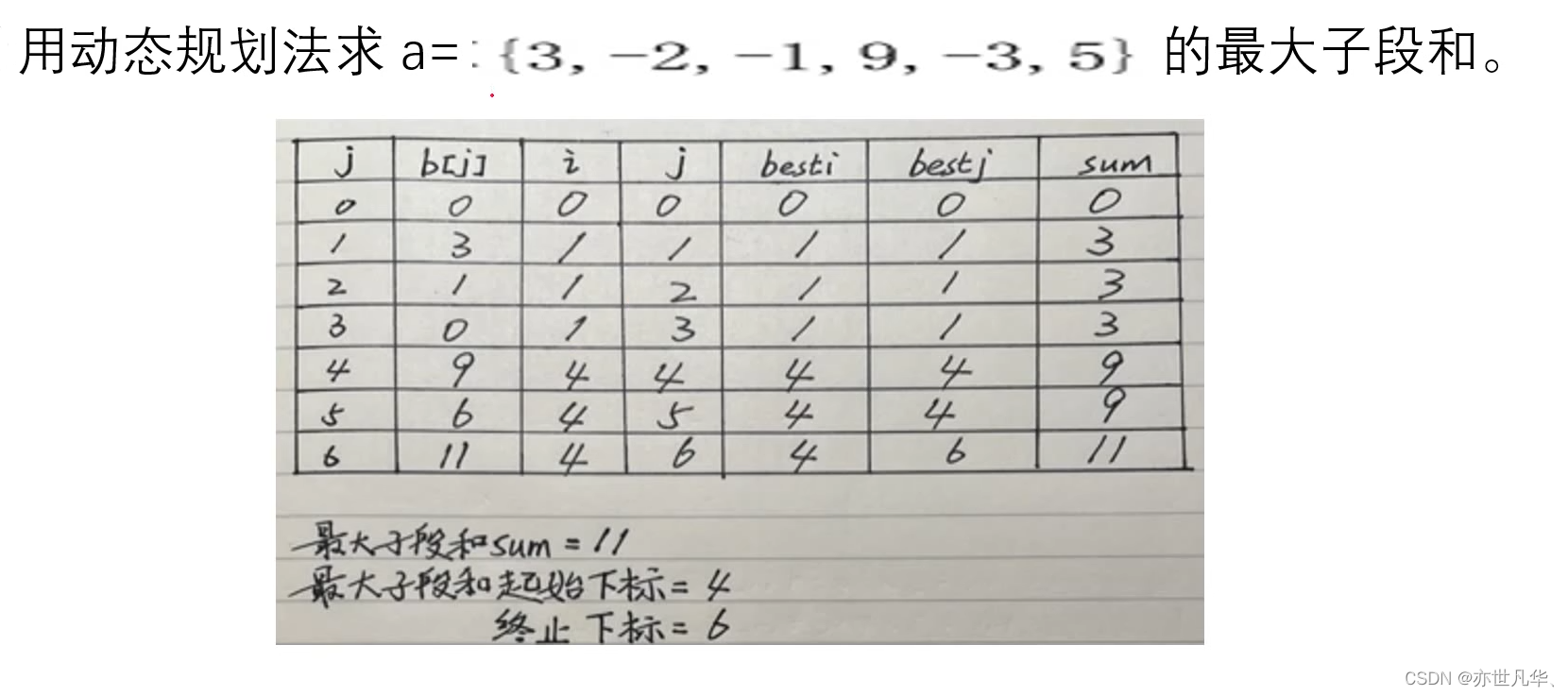
动态规划法



编程题
用回溯法解方程
#include<iostream>
using namespace std;
int a[6] = { 0 };
int solution(int b[], int m, int n)
{
if (m == n)
{
if (b[0] * b[1] - b[2] * b[3] - b[4] == 1)
{
printf("解为a=%d b=%d c=%d d=%d e=%d\n", b[0], b[1], b[2], b[3], b[4]);
}
return 0;
}
for (int i = 1; i <= n; i++)
{
if (a[i] == 0)
{
a[i] = 1;
b[m] = i;
solution(b, m + 1, n);
a[i] = 0;
}
}
}
int main()
{
int c[6];
solution(c, 0, 5);
return 0;
}
动态规划法解决蜘蛛吃蚊子
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cstdlib>
int main(int argc, char** argv)
{
int n = 5, i, j;
if (argc == 2) n = std::stoi(argv[1]);
std::vector<std::vector<int> > dp(n, std::vector<int>(n, 1));
for (i = 1; i < n; ++i)
for (j = 1; j < n; ++j)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
std::cout << "total path for " << n << "x" << n << " grid: " << dp[n - 1][n - 1] << std::endl;
return 0;
}
用分治法解决抛硬币问题
#include <iostream>
#include <vector>
#include <string>
#include <cstdlib>
#include <numeric>
#include <time.h>
int solve(std::vector<int>& a, int low, int high);
int main(int argc, char** argv)
{
int n = 100, m, ans;
if (argc == 2) n = std::stoi(argv[1]);
std::vector<int> a(n, 2);
srand((unsigned)time(NULL));
m = rand() % n; std::cout << "m: " << m << std::endl;
a[m] = 1;
std::cout << "solving ..." << std::endl;
ans = solve(a, 0, n - 1);
std::cout << "coin " << ans << " is fake" << std::endl;
return 0;
}
int solve(std::vector<int>& a, int low, int high)
{
int sum1, sum2, mid, ret_val;
if (low == high) return low; // 只有一个硬币
if (low == high - 1) // 只有两个硬币
{
std::cout << " weighing coin " << low << " and " << high << std::endl;
if (a[low] < a[high]) ret_val = low;
else ret_val = high;
std::cout << " --> coin " << ret_val << " is lighter" << std::endl;
return ret_val;
}
mid = (low + high) / 2;
if ((high - low + 1) % 2 == 0) // 硬币数量为偶数
{
sum1 = std::accumulate(a.begin() + low, a.begin() + mid + 1, 0);
sum2 = std::accumulate(a.begin() + mid + 1, a.begin() + high + 1, 0);
std::cout << " weighing coin " << low << "-" << mid << " and " << mid + 1 << "-" << high << std::endl;
}
else // 硬币数量为奇数
{
sum1 = std::accumulate(a.begin() + low, a.begin() + mid, 0);
sum2 = std::accumulate(a.begin() + mid + 1, a.begin() + high + 1, 0);
std::cout << " weighing coin " << low << "-" << mid - 1 << " and " << mid + 1 << "-" << high << std::endl;
}
std::cout << " sum1=" << sum1 << " , sum2=" << sum2 << std::endl;
if (sum1 == sum2)
{
std::cout << " --> equal" << std::endl;
return mid;
}
else if (sum1 < sum2)
{
std::cout << " --> the former is lighter" << std::endl;
if ((high - low + 1) % 2 == 0) return solve(a, low, mid); // 偶数
else return solve(a, low, mid - 1); // 奇数
}
else
{
std::cout << " --> the latter is lighter" << std::endl;
return solve(a, mid + 1, high);
}
}
用二分法分两边求最大值
#include<stdio.h>
void maxmin(int a, int b, int* min, int* max);
int array[9] = { 1,3,4,5,6,7,8,9,2 };
int main() {
int _max, _min;
maxmin(0, 8, &_min, &_max);
printf("MAX:%d, MIN:%d", _max, _min);
}
void maxmin(int a, int b, int* min, int* max) {
int lmax, lmin, rmax, rmin;
if (a == b) *min = *max = array[a];
else if (a == b - 1) {
if (array[a] < array[b]) {
*min = array[a];
*max = array[b];
}
else {
*min = array[b];
*max = array[a];
}
}
else {
int mid = (a + b) / 2;
maxmin(a, mid, &lmin, &lmax);
maxmin(mid + 1, b, &rmin, &rmax);
if (lmin < rmin) *min = lmin;
else *min = rmin;
if (rmax < lmax) *max = lmax;
else *max = rmax;
}
}