该文章在之前编写并发布过,现在重新编辑一下并纳入到滤波专题中。
之前已经讲过FIR和IIR的概念:
Mr.看海:【滤波专题-第1篇】数字滤波器15分钟入门!——这可能是最简单的FIR有限冲激响应滤波讲解
Mr.看海:【滤波专题-第2篇】数字滤波器15分钟入门!——这可能是最简单的IIR无限冲激响应滤波讲解
从名字上看,“无限冲激响应”和“有限冲激响应”的区别一定在“冲激响应”上。在之前的文章里我们讲到了冲激响应的概念,文章里用被打了一巴掌(单位脉冲)后鼓起来的“包”来描述的冲激响应。
有些人的“包”几分钟可以消肿直至消失,就是有限冲激相应;有些人的“包”虽然会慢慢变小,但是永远不会消失,就是无限冲激响应。
那么问题来了,IIR和FIR数字滤波器有什么区别?
区别一、结构形式
两种滤波器最直观的区别就体现在结构形式上。
这里直接放公式了,公式并不难理解:
IIR的方程中,当前输出y(n)是由当前输入x(n)、过去输入x(n-1)、x(n-2)...、过去输出y(n-1)、y(n-2)...这三类值共同决定的。
而在FIR方程中,则没有过去输出这一项。

IIR的差分方程
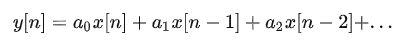
FIR的差分方程
由于IIR的当前输出受到以前输出值的影响,所以它是有反馈的,或者说其输出值是递归的;相对应的,FIR就是无反馈、非递归的。
需要注意的是,上述差分方程中的系数a和b不是单纯的常数。
区别二、相位特性
滤波会引起相位延迟,为什么呢。首先看下图:
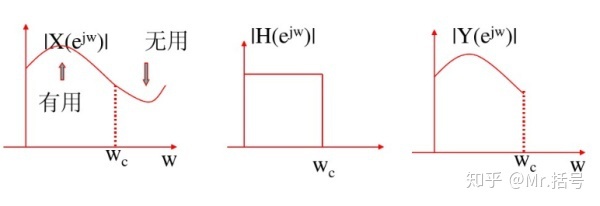
图1*图2=图3
其中三张图分别是原始信号频谱图、滤波器频谱图和滤波后信号的频谱图。图2可以是理想情况下的低通滤波器。图1*图2=图3就是滤波在频域上的表示过程(相乘),也很好理解。不过看到这里大家会想起什么?之前的文章里提到过:频域上相乘即时域上卷积。
暂且把这个卷积写成y(k)=∑h(k)x(n-k)。(对于IIR,k取从0到n;对于FIR,k取从0到N-1)
也就是说对于输出y(k),其值是由其之前N或n个输入点共同决定的,这就是引起相位延迟的原因。

相位延迟
IIR为非线性相位延迟,FIR为线性相位延迟。即IIR的相位延迟会随着输入波形的变化而变化,而FIR的相位延迟为一确定值。FIR的相位补偿只需要对输出结果平移即可,IIR的相位补偿复杂一些,不过在matlab上实现同样很容易。
区别三、稳定性、运算速度、运算误差设计难度
FIR的极点全部在原点(z变换),是稳定的。IIR不一定稳定。
FIR运算速度快,IIR运算速度慢
FIR运算误差小,IIR由于有反馈,可能会产生极限环。
FIR设计难度高,需要借助计算机程序完成,IIR设计难度低。
文章如要转载请私信与我联系,并注明来源知乎专栏与信号处理有关的那些东东作者Mr.括号。
欢迎关注我的公众号“看海的城堡”,微信号为“khscience”,会有更多有趣的东西分享。
参考: