计算步骤
模型框架
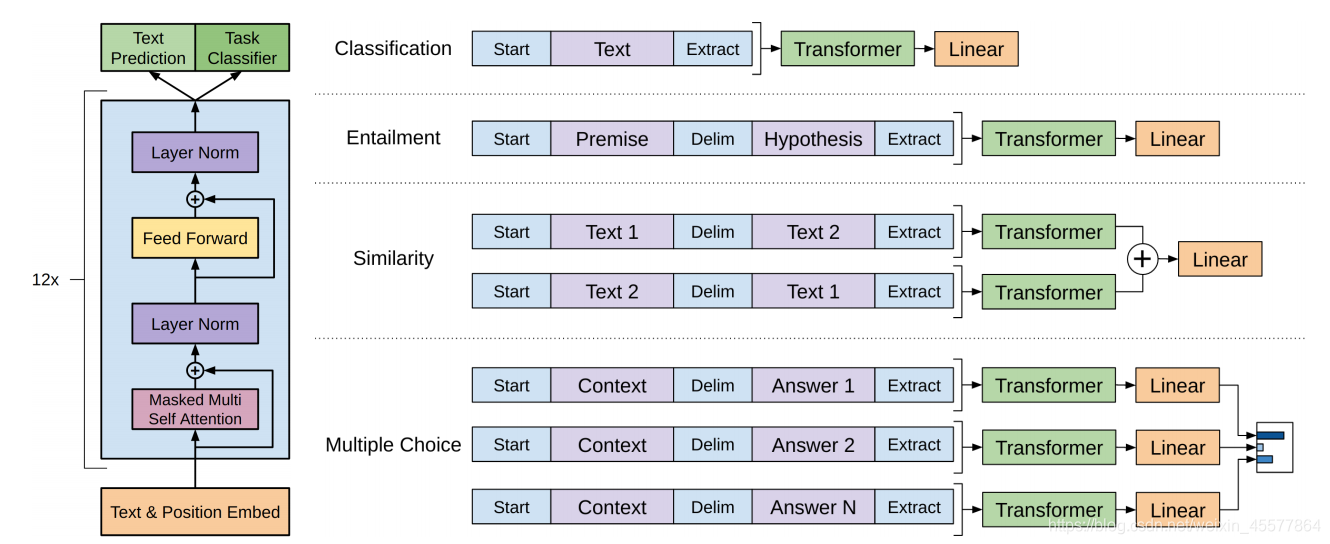
- 输入
- Embedding
- 多层transformer的block (12层)
- 拿到两个输出端结果
- 计算损失
- 反向传播
- 更新参数
下面主要介绍上述步骤中的2.Embedding和3.transformer的block层
Embedding
Embedding层就是以one hot为输入、中间层节点为字向量维数的全连接层。而这个全连接层的参数,就是一个“字向量表”。实现text输入维度的变换。

Embedding操作(此处指text embedding)实际上是一个查表操作,one hot型的矩阵相乘,就像是相当于查表,于是它直接用查表作为操作,而不写成矩阵再运算,这大大降低了运算量。再次强调,降低了运算量不是因为词向量的出现,而是因为把one hot型的矩阵运算简化为了查表操作。
代码部分
def input_emb(self,seqs, segs):
# device = next(self.parameters()).device
# self.position_emb = self.position_emb.to(device)
return self.word_emb(seqs) + self.segment_emb(segs) + self.position_emb
包括text embed和position embed
- text embed
self.word_emb = nn.Embedding(n_vocab,model_dim)
self.word_emb.weight.data.normal_(0,0.1)
self.segment_emb = nn.Embedding(num_embeddings= max_seg, embedding_dim=model_dim)
self.segment_emb.weight.data.normal_(0,0.1)
text embed部分调用nn.Embedding,构造词/段向量矩阵,查表实现降维。
- position embed
self.position_emb = torch.empty(1,max_len,model_dim)
nn.init.kaiming_normal_(self.position_emb,mode='fan_out', nonlinearity='relu')
self.position_emb = nn.Parameter(self.position_emb)
position embed则是初始化一个包含输入序列长度作为维度的矩阵,然后作为参数训练学习位置信息。
Transformer的block层
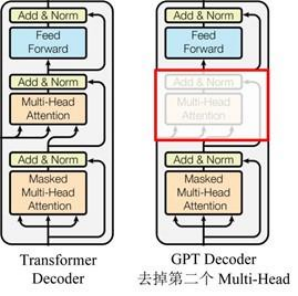
由右上图知,GPT包含的block和Transformer的Decoder比较像,每个block包含两个子层:
- Sublayer1:Masked Multi-Head Attention(mask多头注意力层)
- Sublayer2:Feed Forward Network(FFN层)
每一个子层后均有残差连接和归一化操作
sublayer1:mask多头注意力层
输入: q, k, v, mask
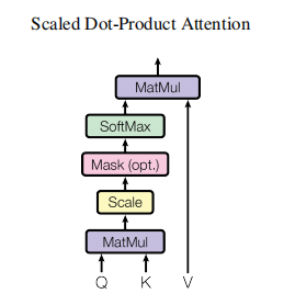
计算注意力(如下图左所示):
- Linear(矩阵乘法)
- Scaled Dot-Product Attention
- Concat(多个注意力的结果)
- Linear(矩阵乘法)
残差连接和归一化操作:Dropout操作 → 残差连接 → 层归一化操作
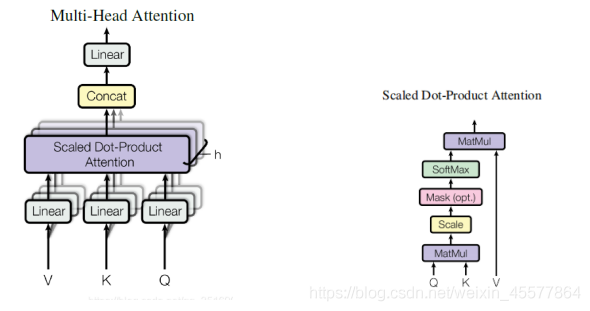
我们以上图中的左图介绍整个注意力层的计算过程
- 矩阵乘法
将输入的Q,K,V与矩阵作乘法,得到新的Q,K,V
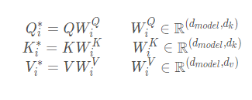
- Scaled Dot-Product Attention
这个操作名字看起来很长,实际上是 点乘+缩放+mask(可选)+Softmax+点乘 来计算注意力值的过程
第一步:Q与K的转置进行点乘,计算Q和K的相似度
第二步:缩放,除以一个比例因子
第三步:Mask矩阵中一部分值(可选,GPT中有此操作)
第四步:Softmax,转化为每个token的概率
第五步:Softmax后的矩阵值点乘V值,每个value通过概率加权,得到注意力分数。
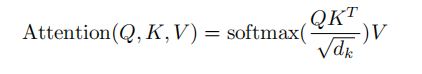
补充:
Mask操作:masked_fill_(mask, value)
掩码操作,用value填充tensor中与mask中值为1位置相对应的元素。mask的形状必须与要填充的tensor形状一致。(这里采用-inf填充,从而softmax之后变成0,相当于看不见后面的词)
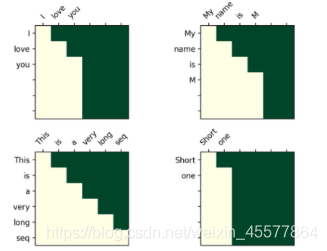
transformer中的mask操作
mask后可视化矩阵:
直观理解是每个词只能看到它之前的词(因为目的就是要预测未来的词嘛,要是看到了就不用预测了)
- Concat操作
综合多个注意力头的结果,实际上是对矩阵做变换:permute,reshape操作,视具体情况降维。(如下图红框中所示)
context = torch.matmul(self.attention,v) # [n, num_head, step, head_dim]
context = context.permute(0,2,1,3) # [n, step, num_head, head_dim]
context = context.reshape((context.shape[0], context.shape[1],-1))
return context # [n, step, model_dim]
- 矩阵乘法
一个Linear层,对注意力结果线性变换
整个mask多头注意力层的代码
def forward(self,q,k,v,mask,training):
# residual connect
residual = q
dim_per_head= self.head_dim
num_heads = self.n_head
batch_size = q.size(0)
# 1.线性变换,linear projection
key = self.wk(k) # [n, step, num_heads * head_dim]
value = self.wv(v) # [n, step, num_heads * head_dim]
query = self.wq(q) # [n, step, num_heads * head_dim]
# split by head
query = self.split_heads(query) # [n, n_head, q_step, h_dim]
key = self.split_heads(key)
value = self.split_heads(value) # [n, h, step, h_dim]
#2.3 Scaled Dot-Product Attention计算注意力分数 + Concat连接多头注意力
context = self.scaled_dot_product_attention(query,key, value, mask) # [n, q_step, h*dv]
#4.Linear层,对注意力结果线性变换
o = self.o_dense(context) # [n, step, dim]
#残差连接和归一化操作
o = self.o_drop(o)
o = self.layer_norm(residual+o)
return o
注意到,最后进行了残差连接和归一化操作,包括:
- Dropout操作
- 残差连接
- 层归一化操作
sublayer2:FFN前馈网络
主要是一个多层感知机结构
- 线性层(矩阵乘法)
- relu函数激活
- 线性层(矩阵乘法)
之后同样进行了残差连接和归一化操作,包括:
- Dropout操作
- 残差连接
- 层归一化操作
class PositionWiseFFN(nn.Module):
def __init__(self,model_dim, dropout = 0.0):
super().__init__()
dff = model_dim*4
self.l = nn.Linear(model_dim,dff)
self.o = nn.Linear(dff,model_dim)
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(model_dim)
def forward(self,x):
#1.2.线性层 + relu
o = relu(self.l(x))
#3.线性层
o = self.o(o)
#4.dropout
o = self.dropout(o)
#5.6.残差连接 + 层归一化
o = self.layer_norm(x + o)
return o # [n, step, dim]