【C++笔试强训】第八天

选择题

解析：函数重载：在相同作用域中，函数名字相同，参数列表不同的一系列函数称之为函数重载。

参数列表的不同具体表现在：参数个数不同、参数类型不同、参数类型次序不同。与函数类型返回值没有关系。

解析：A 引用是给变量取别名，需要知道是给谁取的别名，所以必须初始化，指针不强制要求；

B 引用初始化之后就不能被二次引用，但指针指向的对象可以改变；

C 引用不存在空，指针可以指向空；

D 引用就是变量别名；

E 引用底层使用是使用指针来实现的，引用的本质就是一个指针，所以在传参的时候也是传实参的地址；

F 函数参数可以声明为引用或指针类型。

解析：在类域中，public修饰的成员是公有的，可以在类外被访问；private或protected不可以在类外访问。

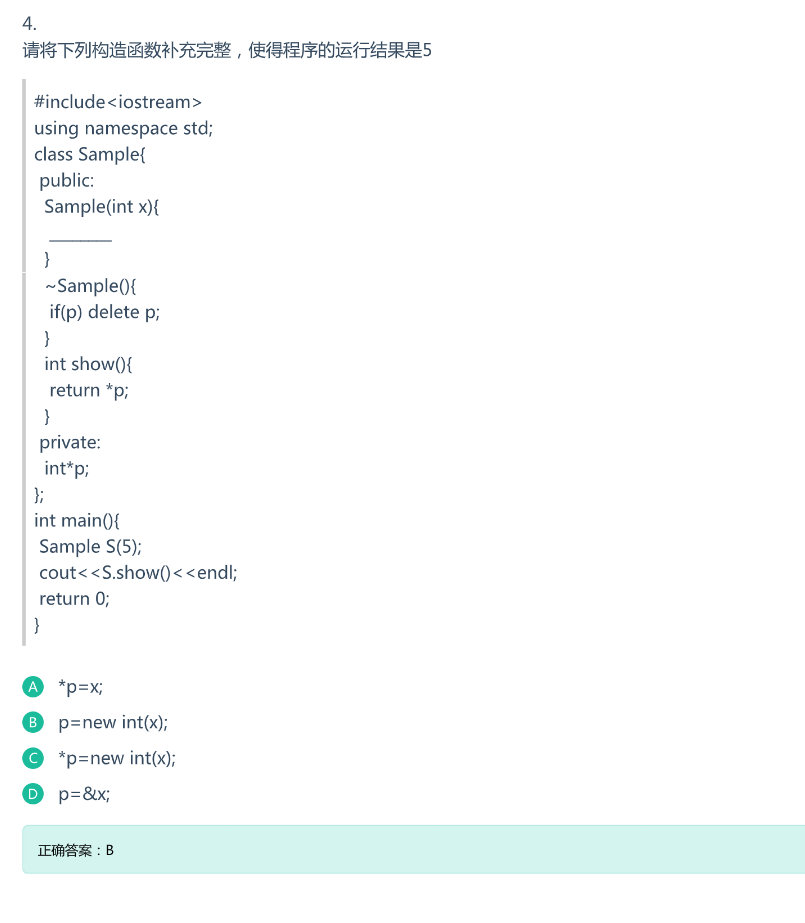
解析：在main函数中Sample S(5)创建对象的时候需要调用构造函数，在析构函数中delete说明需要使用new申请新空间，而p指向新空间的地址，new int(x)表明要给新申请的空间赋值。

解析：拷贝构造函数是一个特殊的构造函数，是单参的，参数的类型必须是类类型&，如果使用传值传参会一直递归，一般情况下会使用const修饰，eg：const A& a；

当用已经存在的对象构造新对象时，编译器会自动调用拷贝构造函数；

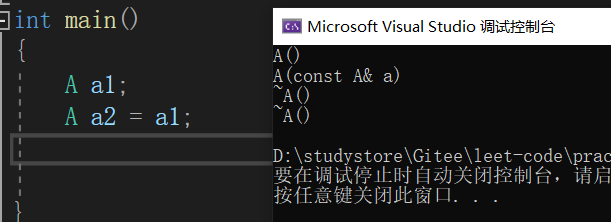
A：当创建一个新的对象时要调用构造函数，但是编译器会做优化，如下图所示，构造+拷贝构造优化为拷贝构造；

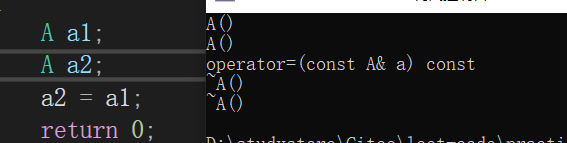
B：将类的一个对象赋值给该类的另一个对象时，调用的是赋值运算符，如下图

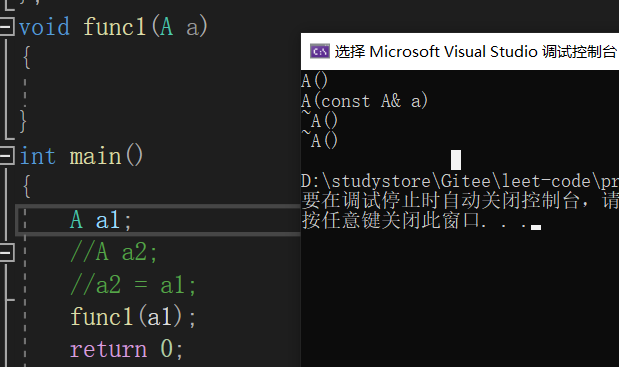
C：函数的形参对象，调用函数进行形参和实参结合时，即对类对象进行函数传参时也会调用拷贝构造函数

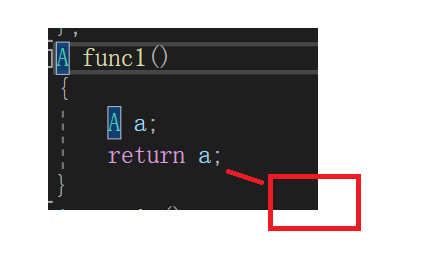
D：函数的返回值是类的对象，函数执行返回调用时；函数执行返回调用时会先进行拷贝构造，将返回值放在一个临时对象中，因为函数执行完栈帧会销毁，所以返回的时候返回的是拷贝构造产生的临时对象。

解析：从main函数中第一条指令开始分析，Widget x调用构造函数；Widget y=f(f(x));先执行里面的f(x)，传参的时候会调用一次拷贝构造，函数内部Widget v(u)创建新对象的时候也会调用一次拷贝构造，Widget w=v的时候也调用一次拷贝构造；return w的时候会调用拷贝构造创建一个临时变量用来返回；到现在调用了4次拷贝构造了，接着执行外面一层函数调用，又是4次拷贝构造；函数调用完成之后，用一个已经存在的对象去创建新对象时，也会调用拷贝构造，所以一共调用了9次拷贝构造。

注意：编译器在调用拷贝对象时会进行一些优化，在返回值的时候我们需要创建临时对象，编译器可能会直接拿着临时对象使用，这样子可以少调用一次，所以可以认为是调用了7次拷贝构造。

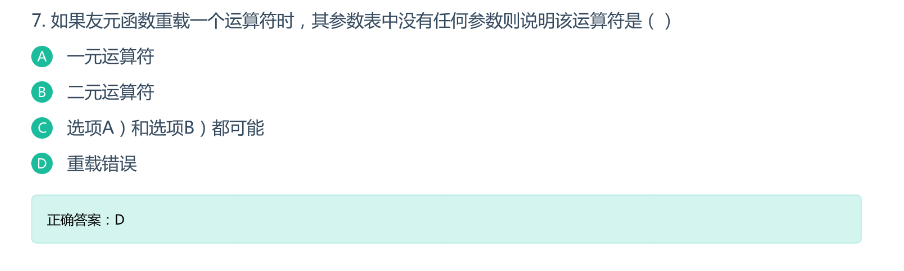
解析：什么时候需要运算符重载？当用户定义了一个类之后，然后想要通过该类的对象直接使用某种运算符时编译器不支持，原因就是类对象中可能有多个成员，在用该类的对象进行相应的运算符操作时，编译器不知道该如何处理。

函数重载运算符，函数形参个数要根据运算符的操作数决定。

运算符重载成类的成员函数时，因为在类里面函数有隐藏的this指针，所以重载运算符时形参数目看起来比该运算符的操作数少1；

重载成类的友元函数时，必须要有一个参数是类类型的对象。

D中没有任何参数明显错误，而且运算符必须要有操作数。

解析：因为先创建A类型的变量，所以先调用A的构造函数；再创建B类型的变量，调用B的构造函数；B先调用析构函数然后是A，可以理解为进栈和出栈：A先进栈，B才进栈，所以要B先出栈，A才能出栈。

解析：在main函数中创建了一个cla类型的对象，然后delete；cla类中的成员变量是静态变量，在类外定义n = 0；new的时候要调用构造函数，delete的时候要调用析构函数，所以最后n还是为0。

解析：C/C++没有内存回收机制，需要考虑内存管理的问题，为了避免内存泄漏，所有在堆上申请的内存都需要用户手动释放；

悬挂引用（悬挂指针）：指向已经释放的地址；首先必须明白空悬指针（悬挂指针）是针对动态内存来说明的：

eg：
	p=new int ;
	delete p;

当我们delete一个指针后，指针值就变为无效了。虽然指针已经无效，但在栈上的指针仍保留着（已经释放了的）动态内存的地址。在delete之后，指针就变成了人们所说的空悬指针，即，指向一块曾经保存数据对象但现在已经无效的内存的指针。

未初始化指针的所有缺点空悬指针也都有。有一种方法可以避免空悬指针的问题：在指针即将要理考其作用域之前释放掉它所关联的内存。这样，在指针关联的内存被释放后，就没有机会使用指针了。如果我们需要保留指针，可以在delete之后将nullptr赋予指针，这样就可以清楚地指出指针不指向任何对象。

程序的动态性越强，内存管理就越重要，内存分配程序的选择也就更重要；

编程题

1.两种排序方法

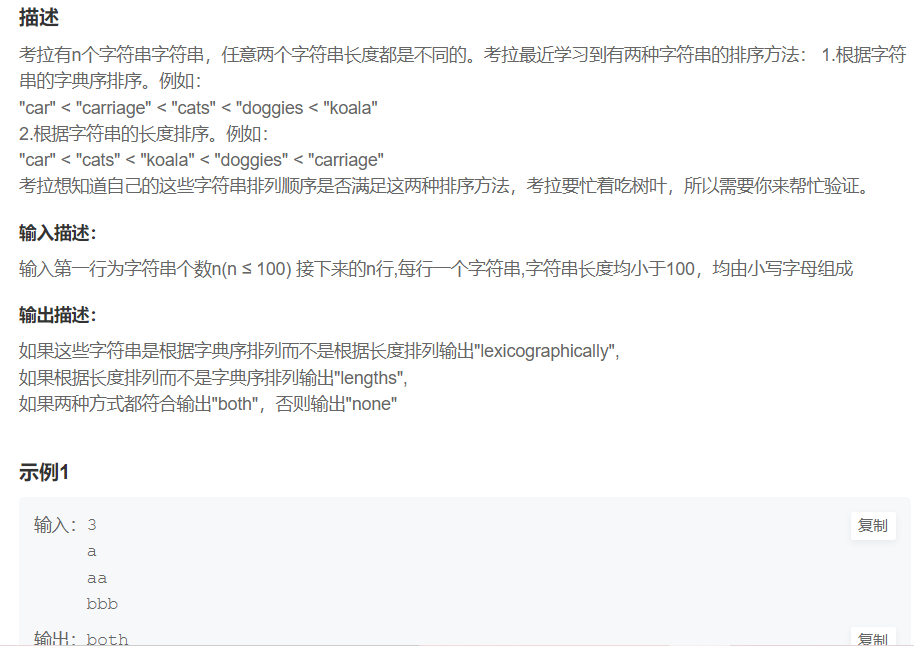
解析：创建string类型的数组，存储数据元素，对数组中每个元素进行长度比较和字符大小比较。需要注意的是当数组中两个字符串中首个字符相同的情况下要继续比较这两个字符串中下一个字符，这样才能确定是不是根据字典序排序。

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int main() {
    int n;
    cin >> n;
    vector<string> s;//定义一个字符指针数组
    s.resize(n);//开辟空间
    for (int i = 0; i < s.size(); i++) {
        cin >> s[i];//使用getline输入的时候会少输入一个字符串，所以当输入的字符串没有空格的时候使用cin
    }
    int i = 0;
    int flag1 = 1;//标记次数，从1开始后面能够和
    int flag2 = 1;
    while (i < n - 1) { //n个元素只需要比较n-1次
        if (s[i][0] < s[i + 1][0]) //等
        {
            flag1++;
        }
        //注意当两个字符串中首个字符相同的时候要继续比较该字符串中下一个位置
        else if(s[i][0] == s[i + 1][0]) {
            int j = 1;
            while (s[i][j] == s[i + 1][j]) { //当不相同时退出循环
                j++;
            }
            if(s[i][j] < s[i + 1][j]){ //再次进行比较
                flag1++;
            }
        }
        if (s[i].length() < s[i + 1].length()) //比较长度
            flag2++;
        i++;//每次增加
    }
    
    //注意下面ifelse条件的顺序不能改变
    if (flag1 == s.size() && flag2 == s.size()) {  //先看两者是否都符合
        cout << "both";
        return  0;
    } 
    else if (flag1 == s.size() && flag2 != s.size()) {
        cout << "lexicographically";
        return 0;
    }
    else if (flag2 == s.size() && flag1 != s.size()) {
        cout << "lengths";
        return 0;
    }
    else {
        cout << "none";
    }
    return 0;
}

答案解析：思路很简单，将接受的字符串都放到vector容器中，利用string的operator>=运算符重载来按ascii比较字符串，利用string的size来比较字符串的长度

#include<iostream>
#include<vector>
#include<string>
using namespace std;
int main()
{
    int n;
    cin>>n;
    vector<string> v;
    v.resize(n);
    for(auto& str : v)
        cin>>str;
    bool lenSym = true, lexSym = true;
    // 这里要注意从i=1开始遍历，前后比较，比较长度
    for(size_t i = 1; i < v.size(); ++i)
    {
        if(v[i-1].size() >= v[i].size())
        {
            lenSym = false;
            break;
        }
    }
    //比较ASCII码
    for(size_t i = 1; i < v.size(); ++i)
    {
        if(v[i-1] >= v[i])
        {
            lexSym = false;
            break;
        }
    }
    if (lenSym&& lexSym)
        cout<<"both"<<endl;
    else if (!lenSym && lexSym)
        cout<<"lexicographically"<<endl;
    else if (lenSym && !lexSym)
        cout<<"lengths"<<endl;
    else if (!lenSym&&!lexSym)
        cout<<"none"<<endl;
    return 0;
}

2.最小公倍数

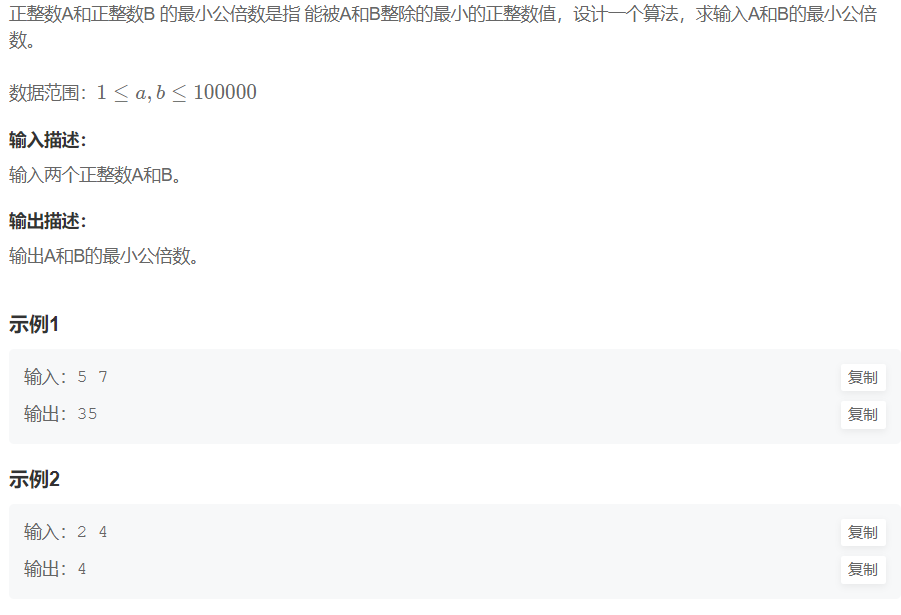
解析：

本题可以使用上图中的第三种方法，扩大法。就是将叫较大数每次扩大1倍，再去%较小数，当取模为0的时候说明该数就是最小公倍数。

#include <iostream>
using namespace std;

int main() {
    int A ,B;
    cin >> A >> B;
    //先找出较大的那一个
    int max = A;
    int min = B;
    if(max < B)
    {
        max = B;
        min = A;
    }
    //从2倍开始比较，找较大数的倍数，然后%较小数，当==0时n就是最小公倍数
    int i = 2;
    int n = max;
    while(n % min)
    {
        n = max*i;
        i++;
    }
    cout << n;
    return 0;
}
// 64 位输出请用 printf("%lld")

答案解析：最小公倍数 = 两数之积除以最大公约数，这里使用碾转相除法进行最大公约数的求解：即a与b的最大公约数可以转化为a、b之间的余数为两者之间最小的数之间的公约数。所以对于输入的两个数进行连续求余，直到余数为0，求余的分母即为结果。

#include<iostream>
using namespace std;
int gcd(int a, int b)
{
    int r;
    while(r = a%b){
        a = b;
        b = r;
    }
    return b;
}
int main()
{
    int a,b;
    while(cin >> a >> b){
        cout << a*b/gcd(a,b) <<endl;
    }
    return 0;
}