模式识别 —— 第五章 数据聚类
文章目录
距离与相似性度量
距离的四条基本公理
- d(x,y) >= 0,对于任意的x,y∈P(两点之间的距离大于0)
- d(x,y) = 0, 当且仅当x=y(相同输入,距离为0)
- d(x,y) = d(y,x),对于任意的x,y∈P(对称性)
- d(x,y) <= d(x,z) + d(z,y),对于任意的x,y,z∈P(满足三角不等式)
闵可夫斯基距离
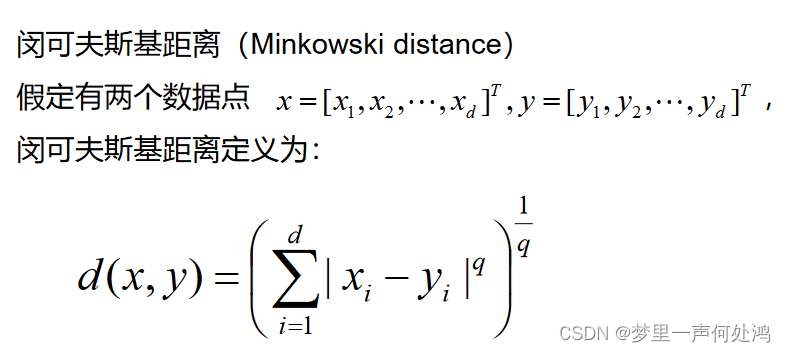
- 当 q = 1 q = 1 q=1时,为曼哈顿距离
- 当 q = 2 q = 2 q=2时,为欧几里得距离
- 当 q q q趋于无穷大时,为切比雪夫距离

欧式距离

马式距离
马氏距离实际上是欧氏距离在多变量下的“加强版”,用于测量点(向量)与分布之间的距离。
欧式距离在多变量距离度量方面有局限性,如下图所示,这是是两个变量的简单散点图。左图是两个变量之间不相关,Point 1和Point 2与分布中心的距离相等。右图是两个变量之间呈正相关。
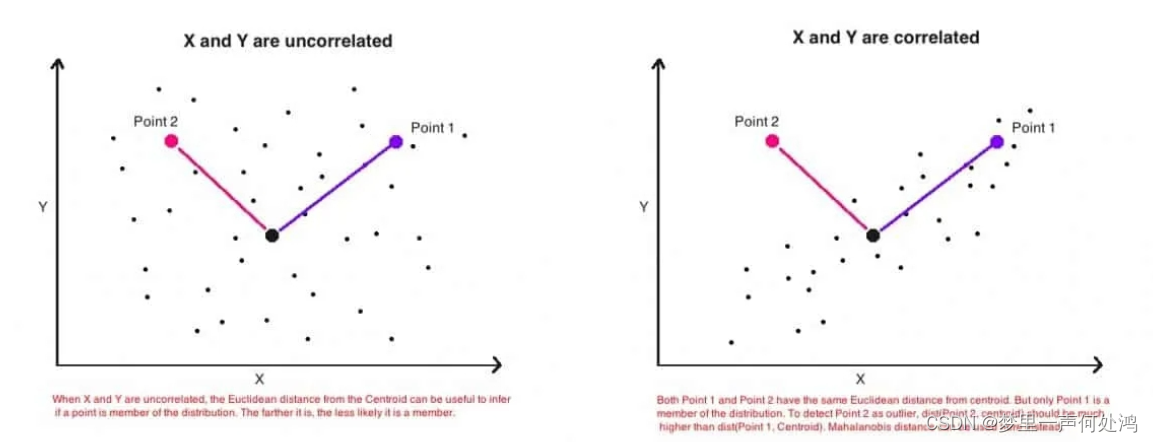
从几何上说,Point 1和Point 2两个点与分布中心的距离相等(欧几里得距离)。但是,即两点到分布的欧几里得距离相等,但实际上只有Point 1(蓝色)更接近该分布。
这是因为,欧几里得距离仅是两点之间的距离,它不考虑数据集中的其余点的分布情况。因此,它不能用来真正判断一个点实际上与点的分布有多接近。所以我们需要的是更健壮的距离度量标准,该度量标准可以精确地表示一个点与分布之间的距离。
计算公式
向量 x x x到一个均值为 μ \mu μ,协方差为 S S S的样本分布的马氏距离计算如下:
d m a h a l = ( x − μ ) S − 1 ( x − μ ) T d_{mahal} = \sqrt{(x - \mu)S^{-1}(x-\mu)^{T}} dmahal=(x−μ)S−1(x−μ)T
其中, ( x − μ ) (x-\mu) (x−μ)本质上是向量与平均值的距离。然后,将其除以协方差矩阵,这实际上是多元变量的常规标准化。如果数据集中的变量高度相关,则协方差将很高。除以较大的协方差将有效缩短距离。同样,如果X不相关,则协方差也不高,距离也不会减少太多。因此,它有效地解决了规模问题以及前文中谈到的变量之间的相关性。
从计算上来说:马氏距离与欧几里得距离相比,有以下不同步骤:
- 首先将列转换为不相关的变量
- 缩放列以使其方差等于1
- 最后,计算出加强版欧几里得距离。
曼哈顿距离
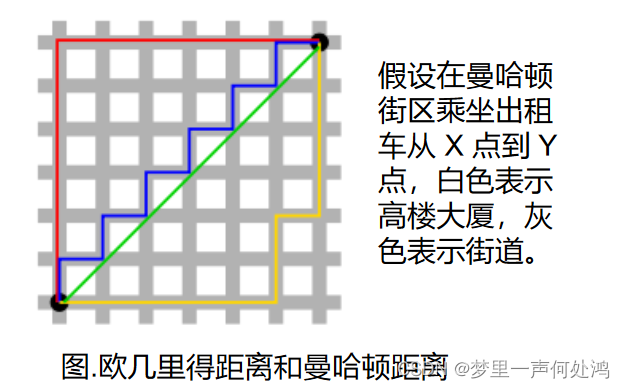
其实通过平移可知就是三角形的两个直角边长度之和。
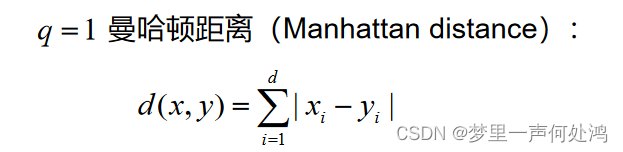
切比雪夫距离

汉明距离

例如:
d(10010,10000) = 1
d(abcbc,abdab) = 3
余弦相似度

余弦相似度与向量的幅值无关,只与向量的方向相关
杰卡德相似系数

KL散度
基于距离阈值的聚类算法
近邻聚类法


最大最小距离算法

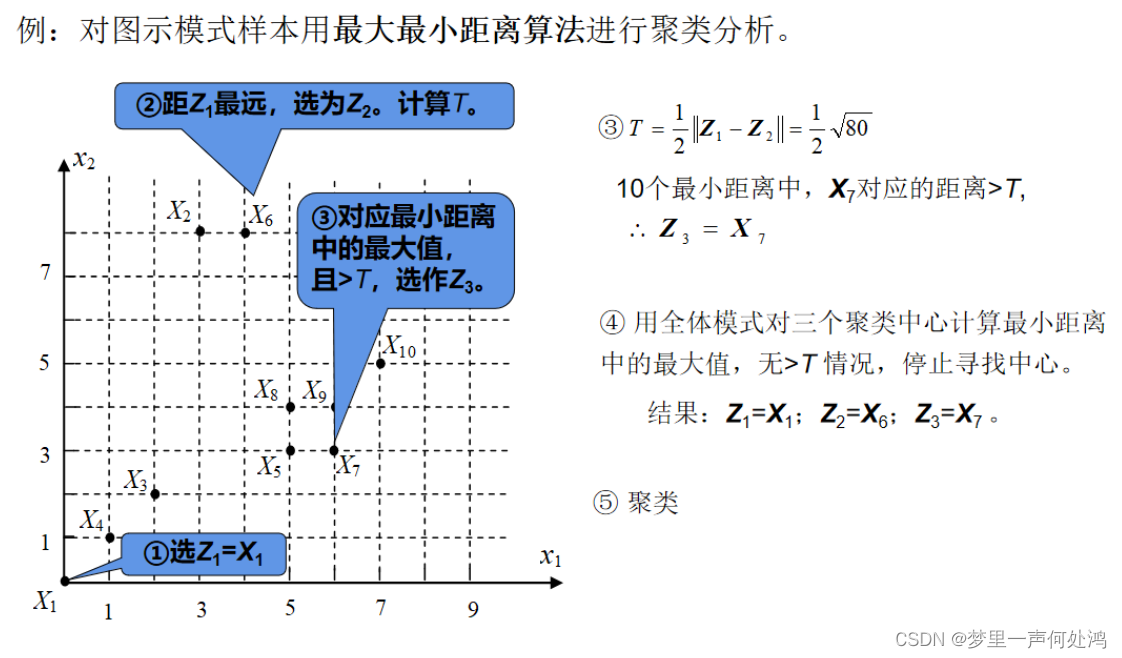
系统聚类法(层次/分级聚类法)

最短距离法
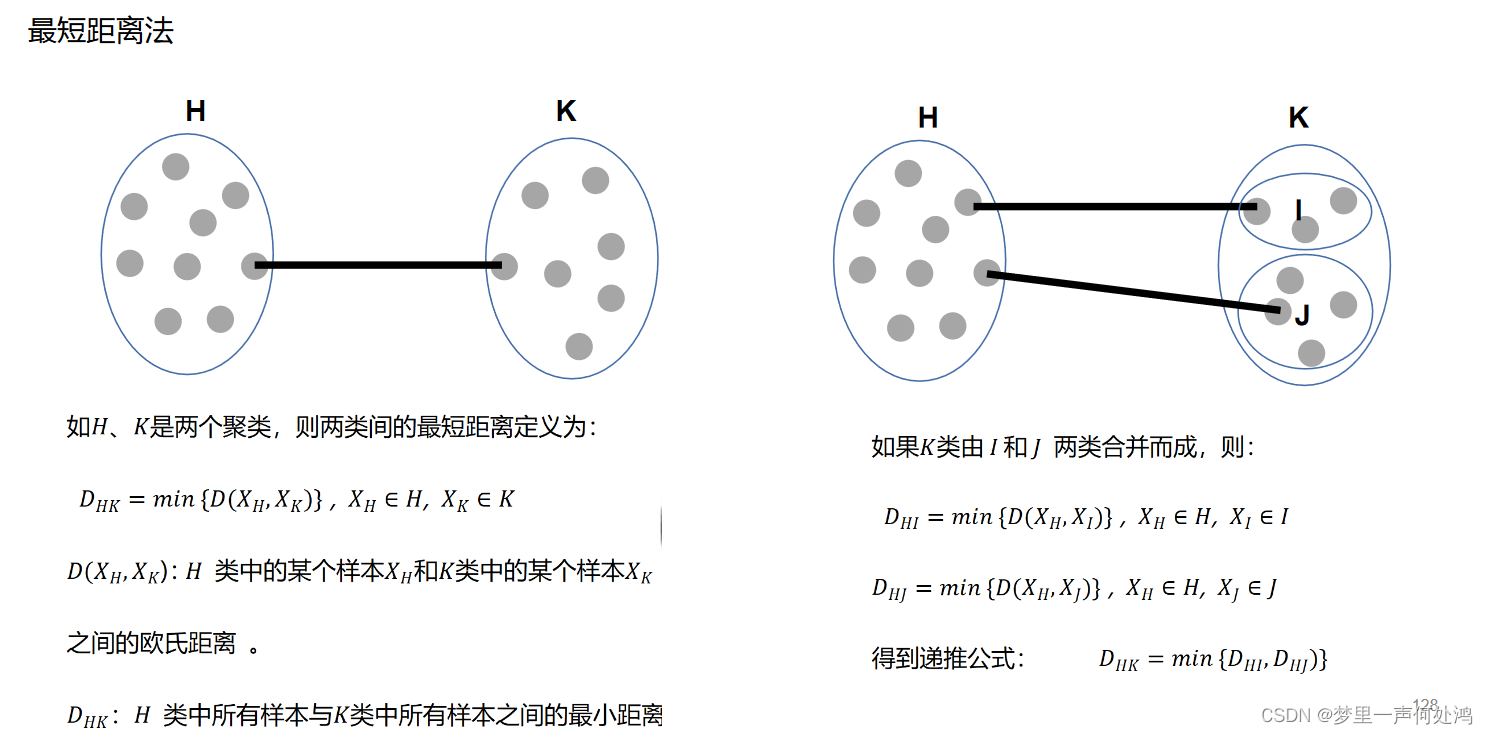
最长距离法

中间距离法(考点)
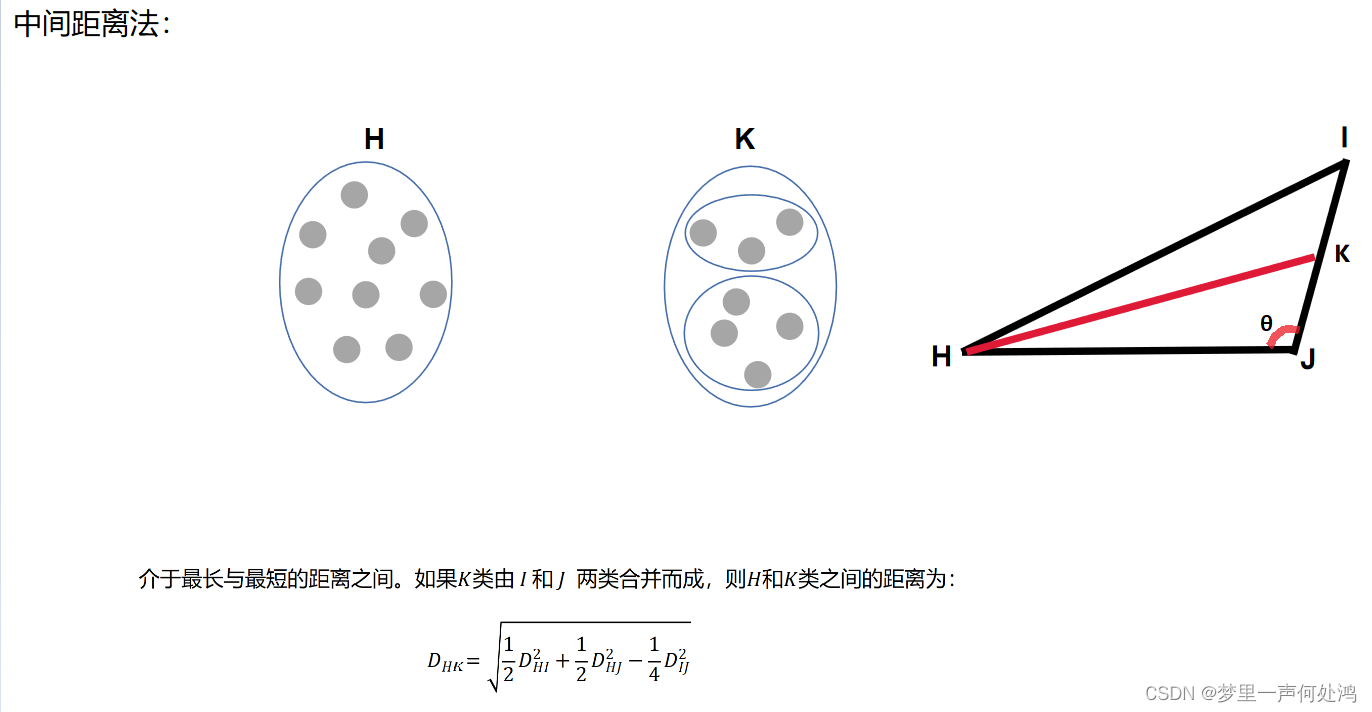
这个老师说要考那个公式的推导,推导如下:
在 Δ \Delta ΔHJK中对于 ∠ \angle ∠ HJI即 θ \theta θ进行余弦定理如下:
c o s θ = H J 2 + J K 2 − H K 2 2 H J × J K = H J 2 + 1 4 J I 2 − H K 2 H J × J I ( 1 ) cos\theta = \frac{HJ^2 + JK^2 - HK^2}{2HJ\times JK} = \frac{HJ^2 + \frac{1}{4}JI^2 - HK^2}{HJ\times JI} (1) cosθ=2HJ×JKHJ2+JK2−HK2=HJ×JIHJ2+41JI2−HK2(1)
在 Δ \Delta ΔHJI中同样对 ∠ \angle ∠ HJI即 θ \theta θ进行余弦定理如下:
c o s θ = H J 2 + J I 2 − H I 2 2 H J × J I ( 2 ) cos\theta = \frac{HJ^2 + JI^2 - HI^2}{2HJ\times JI} (2) cosθ=2HJ×JIHJ2+JI2−HI2(2)
显然,1式与2式是相同的:
H J 2 + 1 4 J I 2 − H K 2 H J × J I = H J 2 + J I 2 − H I 2 2 H J × J I \frac{HJ^2 + \frac{1}{4}JI^2 - HK^2}{HJ\times JI} = \frac{HJ^2 + JI^2 - HI^2}{2HJ\times JI} HJ×JIHJ2+41JI2−HK2=2HJ×JIHJ2+JI2−HI2
解得:
H K = 1 2 H I 2 + 1 2 H J 2 − 1 4 I J 2 HK = \sqrt{\frac{1}{2}HI^2+\frac{1}{2}HJ^2-\frac{1}{4}IJ^2} HK=21HI2+21HJ2−41IJ2
重心法
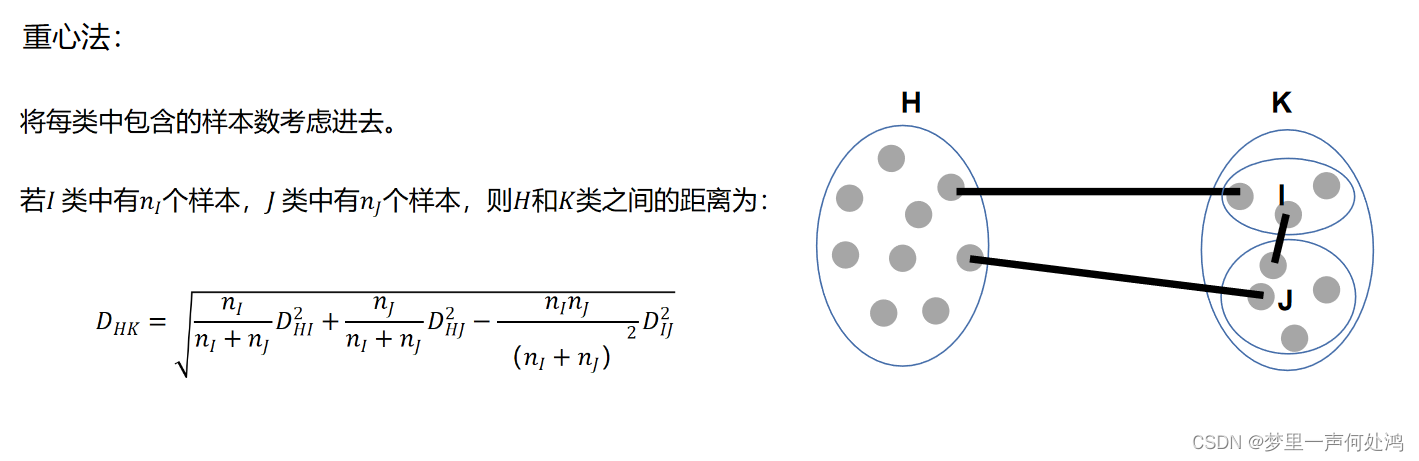
类平均距离法
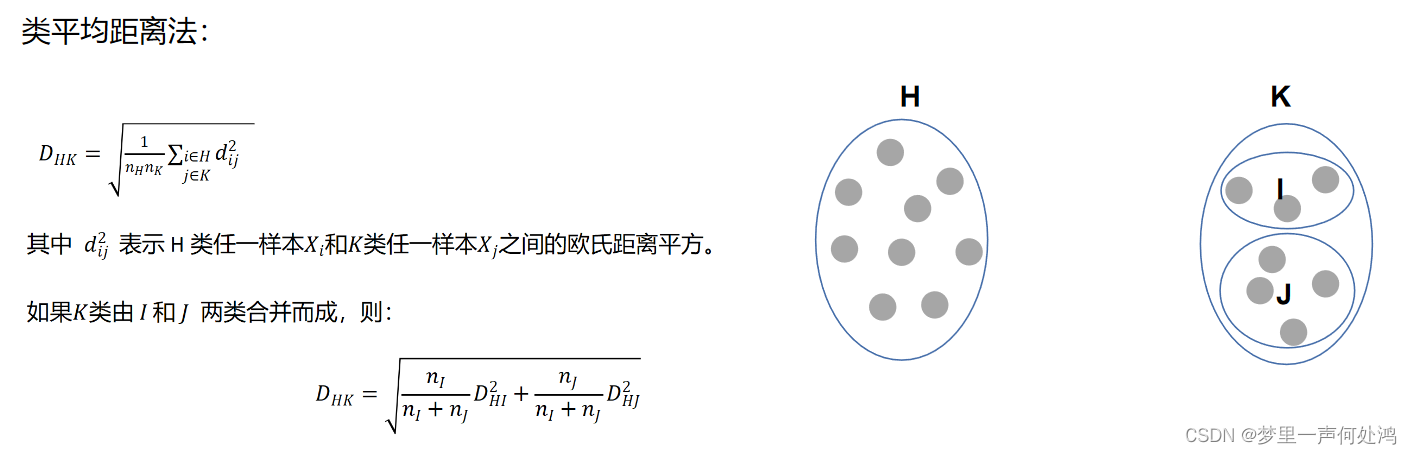
动态聚类方法
K-均值算法 (K-means算法)
 例题:
例题:
随机取2个点
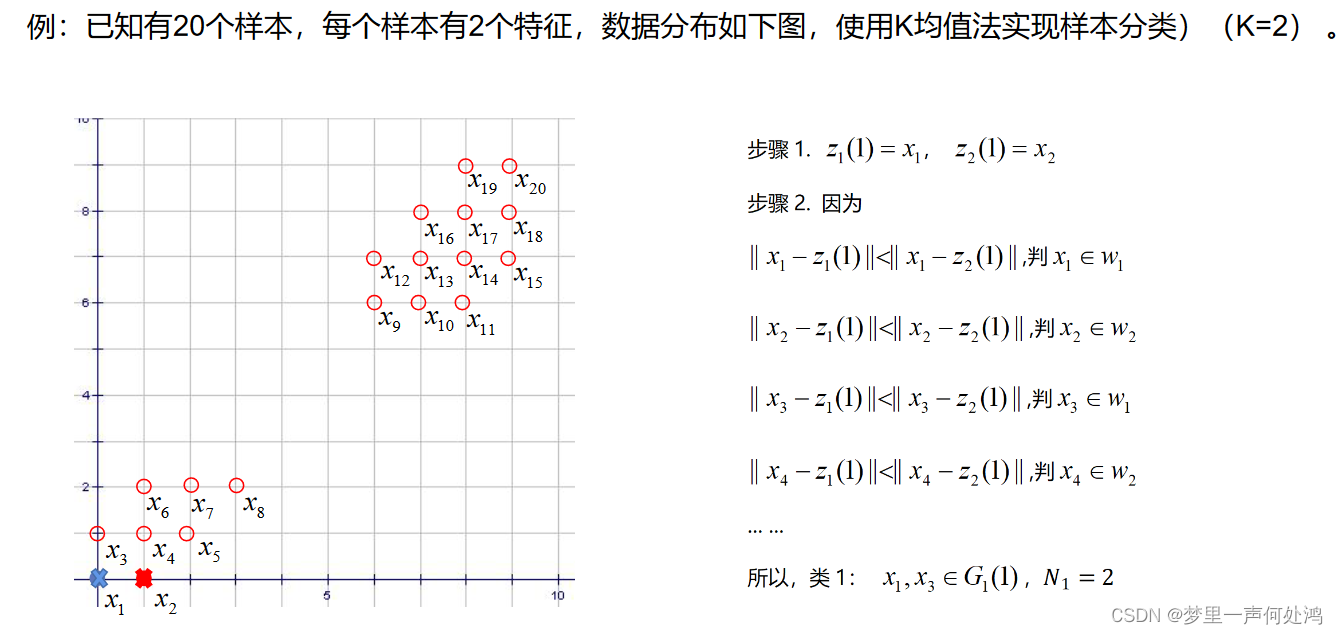 最近距离聚类
最近距离聚类
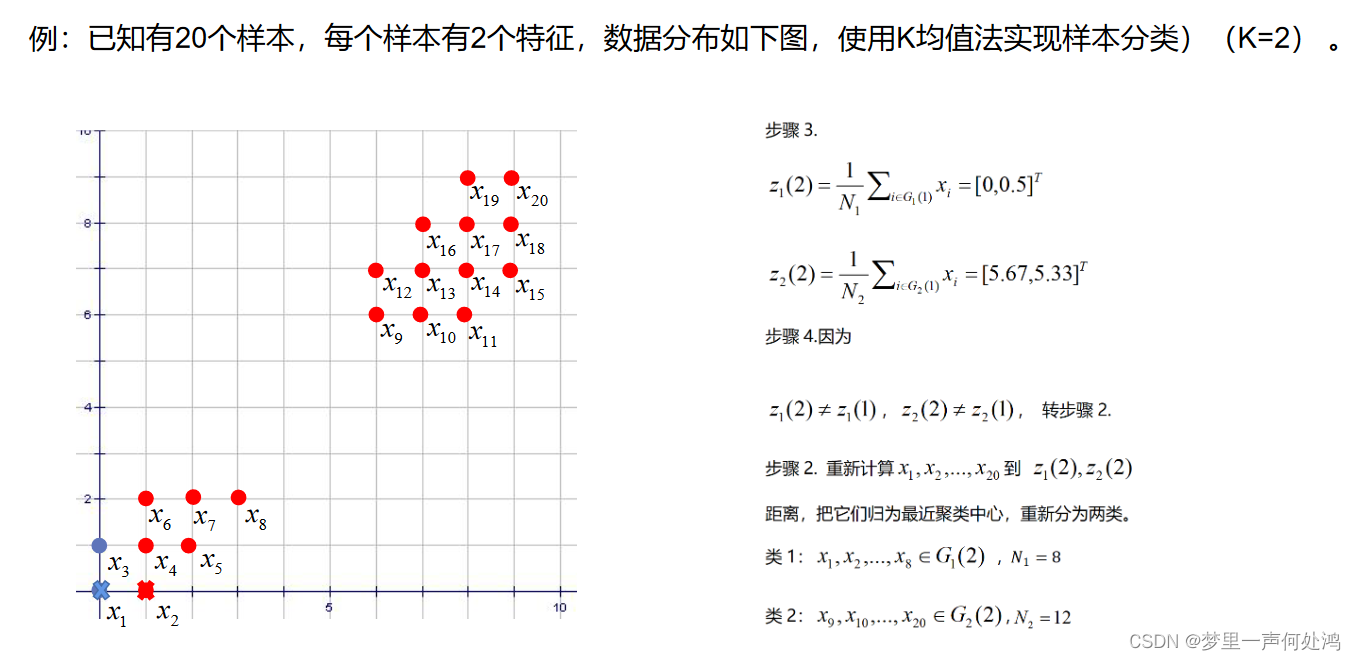 类中心取点
类中心取点
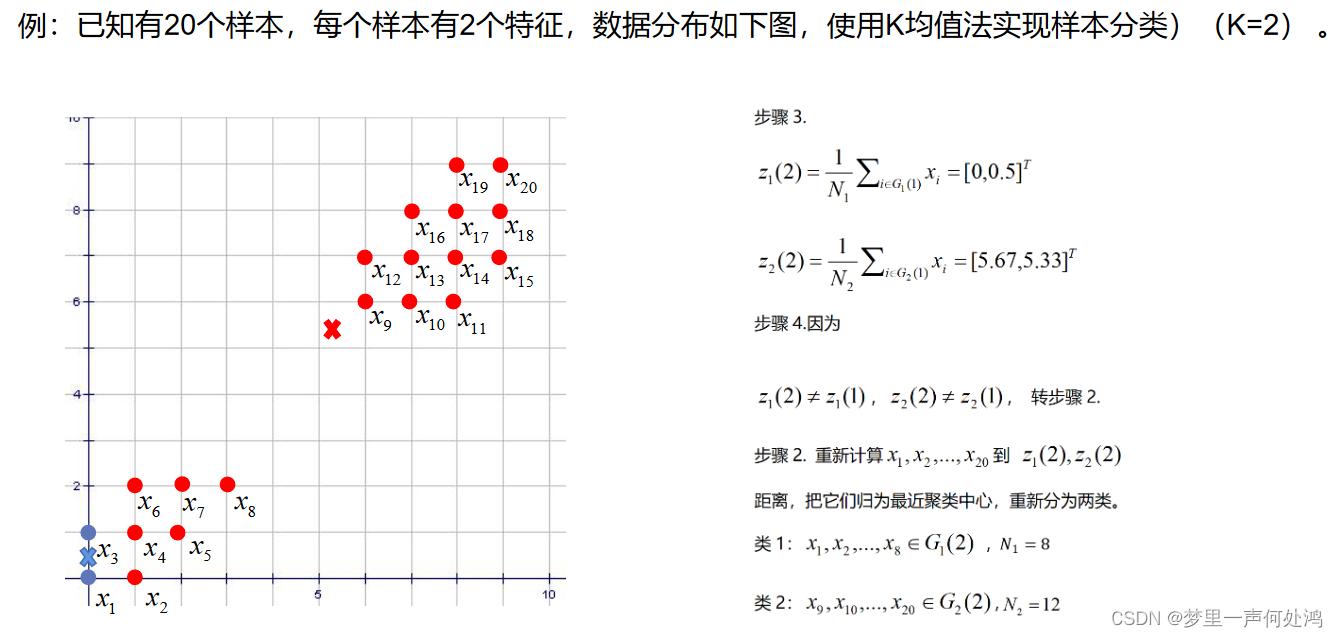 重新最近距离聚类
重新最近距离聚类

重复上述操作至不在变化。
迭代自组织的数据分析算法(ISODATA)







谱聚类
啊啊啊,偷个懒吧。反正这章的考题不考这个,嘻嘻。
