EKF扩展卡尔曼滤波器 - CTRV运动模型 及其代码实现

本文参考了Adam大佬的帖子
https://blog.csdn.net/AdamShan/article/details/78265754
原贴的公式有一点点错误，这里已经修正了，并给出了代码实现。

CTRV模型

我们通常所使用的匀速CV，匀加速CA模型，是线性模型，没有考虑到目标的转向运动，所以在进行目标位置预测的时候会有一些误差。
所以，有一种更精确的模型可以描述目标的运动，也就是恒速度恒角速度运动模型，CTRV。

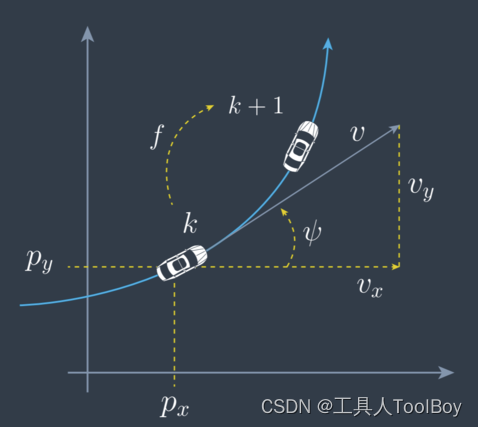
在CTRV中，我们认为目标有位置x，y，速度v（xy合速度），朝向角θ，以及角速度ω。这五个参数组成了状态向量。
$$\overrightarrow{x}(t)=(xyv\theta \omega {)}^T$$
所以，在$\omega$ 不为0的时候，状态向量可以写成这样子：
$$\overrightarrow{\mathrm{x}}(\mathrm{t}+\Delta \mathrm{t})=\mathrm{g}(\mathrm{x}(\mathrm{t}))=\left(\begin{array}{c}\frac{\mathrm{v}}{\omega }\sin (\omega \Delta \mathrm{t}+\theta )-\frac{\mathrm{v}}{\omega }\sin (\theta )+\mathrm{x}(\mathrm{t})\\ -\frac{\mathrm{v}}{\omega }\cos (\omega \Delta \mathrm{t}+\theta )+\frac{\mathrm{v}}{\omega }\cos (\theta )+\mathrm{y}(\mathrm{t})\\ \mathrm{v}\\ \omega \Delta \mathrm{t}+\theta \\ \omega \end{array}\right),\omega \ne 0$$
但是，$\omega$为0的时候，上面的公式分母中会出现0，所以，需要写成这样：
$$\overrightarrow{\mathrm{x}}(\mathrm{t}+\Delta \mathrm{t})=\mathrm{g}(\mathrm{x}(\mathrm{t}))=\left(\begin{array}{c}\mathrm{v}\cos (\theta )\Delta \mathrm{t}+\mathrm{x}(\mathrm{t})\\ \mathrm{v}\sin (\theta )\Delta \mathrm{t}+\mathrm{y}(\mathrm{t})\\ \mathrm{v}\\ \omega \Delta \mathrm{t}+\theta \\ \omega \end{array}\right),\omega =0$$

EKF扩展卡尔曼滤波器

在看本文之前，想必你已经能够理解并且掌握KF滤波器。但是我们知道，KF是一个纯线性滤波器，也就是只能支持匀速和匀加速模型（也就是CV和CA）。如果我们需要引入CTRV，就需要扩展卡尔曼滤波器EKF。那么它是什么原理呢？
我们知道，想要使用卡尔曼滤波器的五个公式，必须保证状态转移矩阵是线性模型，因为误差矩阵只有线性变换之后才能保证还是高斯分布。
所以，我们想要使用非线性的CTRV模型，就必须想一个办法进行近似，让这些方程变成线性方程。
那么方法来了，在大学上过高数的小伙伴一定学过泰勒级数这个神器。泰勒级数的作用是，将一切函数，用导数的方式进行展开，只要展开的级数足够多，最后就可以无限逼近原函数。
$$\mathrm{T}(\mathrm{x})=\mathrm{f}(\mathrm{u})+(\mathrm{x}-\mathrm{u})\mathrm{Df}(\mathrm{u})+\frac{1}{2!}(\mathrm{x}-\mathrm{u}{)}^2{\mathrm{D}}^2\mathrm{f}(\mathrm{u})+\dots$$

我们发现，这里的一阶展开刚好是一个线性函数。CTRV的一阶泰勒展开就是它的近似线性化方程。
但是也可以发现，这是一种有损的近似，展开点距离越远，误差就越大，当展开点足够近的时候，误差就可以忽略。
在自动驾驶领域，由于采样频率通常可以达到20Hz以上，所以一阶泰勒级数可以进行比较准确的近似。
那么剩下的工作就只剩下求一阶导了。我们对卡尔曼滤波中的状态转移矩阵F中的元素，替换为状态转移方程的偏导数，就可以得到雅克比矩阵 $J_F$ 用这个雅克比矩阵替换卡尔曼滤波中的F，就可以完成预测之后的误差更新了。
对于CTRV模型，求导之后的雅克比矩阵如下（$\omega \ne 0$）：
$${\mathrm{J}}_{\mathrm{F}}=\left[\begin{array}{ccccc}1& 0& \frac{1}{\omega }(-\sin (\theta )+\sin (\Delta \mathrm{t}\omega +\theta ))& \frac{\mathrm{v}}{\omega }(-\cos (\theta )+\cos (\Delta \mathrm{t}\omega +\theta ))& \frac{\Delta \mathrm{t}\mathrm{v}}{\omega }\cos (\Delta \mathrm{t}\omega +\theta )-\frac{\mathrm{v}}{{\omega }^2}(-\sin (\theta )+\sin (\Delta \mathrm{t}\omega +\theta ))\\ 0& 1& \frac{1}{\omega }(\cos (\theta )-\cos (\Delta \mathrm{t}\omega +\theta ))& \frac{\mathrm{v}}{\omega }(-\sin (\theta )+\sin (\Delta \mathrm{t}\omega +\theta ))& \frac{\Delta \mathrm{t}\mathrm{v}}{\omega }\sin (\Delta \mathrm{t}\omega +\theta )-\frac{\mathrm{v}}{{\omega }^2}(\cos (\theta )-\cos (\Delta \mathrm{t}\omega +\theta ))\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& \Delta \mathrm{t}\\ 0& 0& 0& 0& 1\end{array}\right]$$
对于$\omega =0$ :
$${\mathrm{J}}_{\mathrm{F}}=\left[\begin{array}{ccccc}1& 0& \Delta \mathrm{t}\cos (\theta )& -\Delta \mathrm{t}\mathrm{v}\sin (\theta )& 0\\ 0& 1& \Delta \mathrm{t}\sin (\theta )& \Delta \mathrm{t}\mathrm{v}\cos (\theta )& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& \Delta \mathrm{t}\\ 0& 0& 0& 0& 1\end{array}\right]$$
上面的公式基于原贴，已经对原贴公式的一些错误进行了修正。
在实际应用中，我们收到的传感器感知结果都是基于笛卡尔坐标系的，也就是线性观测。那么我们的观测矩阵还保持不变，不需要求雅克比。（如果你的观测值基于极坐标，那么就需要按照原贴的方法求解了。）

例如，我们的观测值只有位置坐标$x$ $y$，观测矩阵$H$如下：
$$J_H=\mathrm{H}=\left[\begin{array}{lllll}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\end{array}\right]$$
总结一下，对于CTRV的EKF，其步骤和KF是一样的，还是那五步，只不过变成了如下的过程：
$${\mathrm{x}}_{\mathrm{k}+1}=\mathrm{g}\left({\mathrm{x}}_{\mathrm{k}},\mathrm{u}\right)$$
$${\mathrm{P}}_{\mathrm{k}+1}={\mathrm{J}}_{\mathrm{F}}{\mathrm{P}}_{\mathrm{k}}{\mathrm{J}}_{\mathrm{F}}^{\mathrm{T}}+\mathrm{Q}$$
$$K_k=P_k{J}_H^T{\left(J_H{P}_k{J}_H^T+R\right)}^{-1}$$
$$x_k=x_k+K_k\left(z_k-h\left(x_k\right)\right)$$
$${\mathrm{P}}_k=\left(I-K_k{J}_H\right)P_k$$

代码实现

求雅克比矩阵最好通过ceres库来进行。但是，我们其实只需要CTRV，所以不如直接手写。
这里我只做了J_f的实现，供大家参考。
由于观测值只有XY，观测方程实际上还是线性的，所以不需要J_h，直接用原来的H即可 ($J_H=H$) 。

void EKF::predict_ctrv() {
    
    
  double dt = 0.1;
  double x = x_hat(0);
  double y = x_hat(1);
  double v = x_hat(2);
  double yaw = x_hat(3);
  double yaw_rate = x_hat(4);
  Eigen::MatrixXd J_f(5, 5);
  if (yaw_rate > 0.000001) {
    
    
  //这是yaw_rate（omega）不为0的情况
    double J_x_x = 1;
    double J_x_y = 0;
    double J_x_v = (1 / yaw_rate) * (sin(yaw + yaw_rate * dt) - sin(yaw));
    double J_x_yaw = (v / yaw_rate) * (cos(yaw + yaw_rate * dt) - cos(yaw));
    double J_x_yaw_rate = dt * (v / yaw_rate) * cos(yaw + yaw_rate * dt) - ((v / (yaw_rate * yaw_rate)) * (sin(yaw + yaw_rate * dt) - sin(yaw)));
    double J_y_x = 0;
    double J_y_y = 1;
    double J_y_v = (1 / yaw_rate) * (cos(yaw) - cos(yaw + yaw_rate * dt));
    double J_y_yaw = (v / yaw_rate) * (sin(yaw + yaw_rate * dt) - sin(yaw));
    double J_y_yaw_rate = dt * (v / yaw_rate) * sin(yaw + yaw_rate * dt) - ((v / (yaw_rate * yaw_rate)) * (cos(yaw) - cos(yaw + yaw_rate * dt)));
    J_f << J_x_x, J_x_y, J_x_v, J_x_yaw, J_x_yaw_rate, J_y_x, J_y_y, J_y_v, J_y_yaw, J_y_yaw_rate, 0, 0, 1, 0, 0, 0, 0, 0, 1, dt, 0, 0, 0, 0, 1;
    //状态向量的预测直接用状态转移方程
    x = x + v / yaw_rate * (sin(yaw + yaw_rate * dt) - sin(yaw));
    y = y + v / yaw_rate * (-cos(yaw + yaw_rate * dt) + cos(yaw));
    v = v;
    yaw = yaw + yaw_rate * dt;
    yaw_rate = yaw_rate;
    x_hat << x, y, v, yaw, yaw_rate;
    //协方差矩阵的更新用上面求好的雅克比矩阵
    P = J_f * P * J_f.transpose() + Q;
  } else {
    
    
  //这是yaw_rate（omega）为0的情况
    double J_x_x = 1;
    double J_x_y = 0;
    double J_x_v = dt * cos(yaw);
    double J_x_yaw = -1 * dt * v * sin(yaw);
    double J_x_yaw_rate = 0;
    double J_y_x = 0;
    double J_y_y = 1;
    double J_y_v = dt * sin(yaw);
    double J_y_yaw = dt * v * cos(yaw);
    double J_y_yaw_rate = 0;
    J_f << J_x_x, J_x_y, J_x_v, J_x_yaw, J_x_yaw_rate, J_y_x, J_y_y, J_y_v, J_y_yaw, J_y_yaw_rate, 0, 0, 1, 0, 0, 0, 0, 0, 1, dt, 0, 0, 0, 0, 1;
    x = x + v * cos(yaw) * dt;
    y = y + v * sin(yaw) * dt;
    v = v;
    yaw = yaw + yaw_rate * dt;
    yaw_rate = yaw_rate;
    x_hat << x, y, v, yaw, yaw_rate;
    P = J_f * P * J_f.transpose() + Q;
  }
}