初识贝塞尔（bezier）曲线

---

资料援引

B站视频：wow，神奇的贝塞尔曲线！

博客：贝塞尔曲线简单介绍

知乎：曲线篇: 贝塞尔曲线

---

贝塞尔曲线的用途

• 基于对汽车的的车身结构进行流体化设计而诞生
• 处理视频状态点之间的图像变化
• 随心所欲绘制曲线，比如：

---

一阶贝塞尔（bezier）曲线

如上，$P_0$、$P_1$ 两点构成了一条线段，而我们可以通过一个函数——线性插值（lerp），来根据一个 $t$ 值（$t\in [0,1]$） 得到线段上一点 $P$（图中一直在滑动的点）。而 $P$ 的运动轨迹（红线），便是一阶贝塞尔线段（曲线）。线性插值的数学形式（一阶贝塞尔曲线公式）为：

$$P=lerp(P_0，P_1，t)=(1-t)P_0+t{P}_1$$

一阶贝塞尔曲线有两个端点（$P_0$、$P_1$ ），0个控制点。

---

二阶贝塞尔（bezier）曲线

如上，假设现在有点 $P_2$ ，它与 $P_1$ 构成了新的线段，我们得到两个 一阶插值点（$Q_1$、$Q_2$），它们构成了绿色线段，值得注意的是，两个插值点具有相同的 $t$ 值。

而此时我们在绿色线段上生成一个 二阶插值点（$P$），并让它具有 与两个一阶插值点相同的$t$ 值。 那么该点的运动轨迹就是 二阶贝塞尔曲线。其公式推导为：

• 绿色线段左端点的运动轨迹：

$$Q_1=(1-t)P_0+t{P}_1$$

• 绿色线段右端点的运动轨迹：

$$Q_2=(1-t)P_1+t{P}_2$$

• 二阶贝塞尔曲线公式：

$$P=(1-t)Q_1+t{Q}_2$$
$$=(1-t)((1-t)P_0+t{P}_1)+t((1-t)P_1+t{P}_2)$$
$$=(1-t{)}^2{P}_0+2t(t-1)P_1+t^2{P}_2$$

二阶贝塞尔曲线有两个端点（$P_0$、$P_2$），一个控制点（$P_1$）。

---

三阶贝塞尔（bezier）曲线

经过对一阶、二阶贝塞尔曲线的研究学习，我们能知道贝塞尔曲线通过在两点之间再采点的方式实现降阶，每一次选点都是一次的降阶。

• $P_0$、$P_1$、$P_2$、$P_3$ 通过生成插值点 $Q_1$、$Q_2$、$Q_3$ 来构成二阶贝塞尔（绿色线段）
• 在此基础上生成插值点 $O_1$、$O_2$ 来构成一阶贝塞尔（蓝色线段）
• 之后以 $O_1$、$O_2$ 上的插值点 $P$ 的运动轨迹来生成三阶贝塞尔曲线。

公式推导过程同二阶贝塞尔曲线，因此不做赘述，直接贴出公式：

$$P=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3$$

三阶贝塞尔曲线有两个端点（$P_0$、$P_3$），两个控制点（$P_1$、$P_2$）。

---

高阶贝塞尔（bezier）曲线

• 四阶贝塞尔曲线示意图：

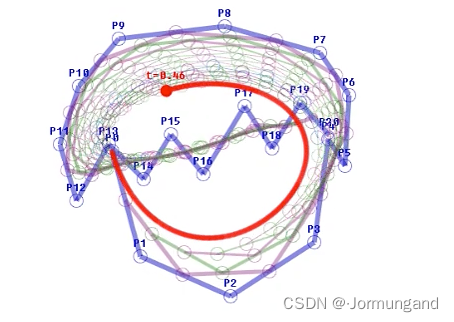
• 五阶贝塞尔曲线示意图：

• 高阶贝塞尔曲线公式：

$$P(t)=\sum _{i=0}^n{P}_i{B}_{i,n}(t)，t\in [0,1]$$

$$B_{i,n}(t)=C_n^i{t}^i(1-t{)}^{n-i}=\frac{n!}{i!(n-i)!}{t}^i(1-t{)}^{n-i}，【i=0,1,...,n】$$

---

三阶贝塞尔曲线求插值（Slerp）

在熟悉了贝塞尔曲线的相关概念之后，我们来了解一下它的具体应用。通常它的应用场景是：

已知两个端点和两个控制点的情况下，根据 动画进度向量 $P_x$ 求 $t$，再由 $t$ 确认的曲线求 $P_y$。

回顾一下三阶贝塞尔曲线公式：
$$P=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3$$

公式中的 $P_0$、$P_1$ 等都是二维向量，由两个一维向量 $P_x$ 和 $P_y$ 构成。而我们根据 $t$ 求 $P$，本质上是根据 $t$ 来求一个坐标 $(x,y)$。因此，可将公式拆解在两个一维向量上：
$$y=(1-t{)}^3{P}_{y0}+3t(1-t{)}^2{P}_{y1}+3t^2(1-t)P_{y2}+t^3{P}_{y3}$$

$$x=(1-t{)}^3{P}_{x0}+3t(1-t{)}^2{P}_{x1}+3t^2(1-t)P_{x2}+t^3{P}_{x3}$$

而由于我们在处理动画时通常起点 $P_0$ 和终点 $P_3$ 都是可以确定的【$P_0(0,0)、P_3(1,1)$】，因此上述公式可以化简为（以 $x$ 举例，$y$ 同理）：

$$x=3t(1-t{)}^2{P}_{y1}+3t^2(1-t)P_{y2}+t^3$$

完全展开：
$$=3P_{y1}t-6P_{y1}{t}^2+3P_{y1}{t}^3+3P_{y2}{t}^2-3P_{y2}{t}^3+t^3$$

提取三次方系数 $a$：
$$a=3P_{y1}-3P_{y2}+1$$

提取二次方系数 $b$：
$$b=3P_{y2}-6P_{y1}$$

提取一次方系数 $c$：
$$c=3P_{y1}$$

将公式简化为：
$$x=a{t}^3+b{t}^2+ct$$

移动 $x$，将公式变为一元三次方程：
$$a{t}^3+b{t}^2+ct-x=0$$

此时，就可以通过卡尔丹公式根据 $x$ 求出来 $t$。之后根据 $t$ 可以求得 $y$：
$$y=(1-t{)}^3{P}_{y0}+3t(1-t{)}^2{P}_{y1}+3t^2(1-t)P_{y2}+t^3{P}_{y3}$$

代码实现：

double SlerpWithCubicBazier(double pX1, double pY1, double pX2, double pY2, double x) {
    
    
    // x为动画进度，并不是t，t只是一个参数，先根据x求t，再由t确认的曲线上求y
    // 参考 https://github.com/gre/bezier-easing/blob/master/src/index.js
    double t = 0.0;
    if (x <= 0.0) {
    
    
        t = 0.0;
    }else if (x >= 1.0) {
    
    
        t = 1.0;
    }else {
    
    
        // x = (1-t)^3*P0x + 3*(1-t)^2*t*P1x + 3*(1-t)*t^2*P2x + t^3*P3x
        // 提取系数：
        double a = 0.0 + 3 * pX1 - 3 * pX2 + 1.0;
        double b = 3 * 0.0 - 6 * pX1 + 3 * pX2;
        double c = 0.0 + 3 * pX1;
        // 公式可化简为： x = at^3 + bt^2 + ct
        // 转换为基于 t 的一元三次方程：at^3 + bt^2 + ct - x = 0
        double d = 0 - x;

        // 那么就可以通过 SolveCubic 函数根据a、b、c、d四个系数来求解一元三次方程的一个实根
        // 可能该一元三次方程的根不止一个，但不重要，即使有多个根我们也只需要其中之一，且要求这个根是在 0～1 之间的，符合 t 的取值范围要求，如果没有根/没有符合要求的根我们会返回 -1
        double tTemp = SolveCubic(a, b, c, d);
        if (tTemp == -1) {
    
    
            return -1;
        }
        t = tTemp;
    }
    
    // Gy(t) = P0*(1-t)^3 + 3*P1*t*(1-t)^2 + 3*P2*t^2*(1-t) + P3*t^3  t[0,1]
    // PY0=0.0 PY3=1.0
    double coef1 = 0.0 * (1.0 - t) * (1.0 - t) * (1.0 - t);
    double coef2 = pY1 * 3 * t * (1.0 - t) * (1.0 - t);
    double coef3 = pY2 * 3 * t * t *  (1.0 - t);
    double coef4 = 1.0 * t * t * t;
    
    double gt = coef1 + coef2 + coef3 + coef4;
    return gt;
}

SolveCubic 函数的具体实现如下，值得注意的是，并不能简单的将此函数的作用等同于求解一元三次方程，本函数的本质作用是贝塞尔曲线中根据 x 求出 t，这两者有什么区别呢？举个具体的例子，下面的代码第 5 行有这样的语句：

if (d == 0) return 0;

• 在 d=0 的情况下，普通一元三次方程是可以继续求解的；
• 但是在 SlerpWithCubicBazier 调用 SolveCubic 时，是以 $d=0-x$ 的形式传值的，$d=0$ 代表 $x=0$，此时曲线位于起点，t 的值可以确定，无需通过解方程获得，即 $t=0$。

double FCPSolveCubic(double a, double b, double c, double d) {
    
    
    /* a=0 视为一元二次方程式 */
    if (a == 0) return FCPSolveQuadratic(b, c, d);
    /* d=0表明x=0，则t=0*/
    if (d == 0) return 0;
    
    /* 将三次方的系数变为1，方便后续判别式中的计算，即不用考虑 a^2 这一项了 */
    b /= a;
    c /= a;
    d /= a;
    /* q和r对应求根公式中的p和q，dis即是求根公式的判别式 △ */
    double q = (3.0 * c - FCPSquared(b)) / 9.0;
    double r = (-27.0 * d + b * (9.0 * c - 2.0 * FCPSquared(b))) / 54.0;
    double disc = FCPCubed(q) + FCPSquared(r);
    double term1 = b / 3.0;
    
    if (disc > 0) {
    
    
        /* 运用卡尔丹公式求得一个实根 */
        double s = r + sqrtf(disc);
        s = (s < 0) ? - FCPCubicRoot(-s) : FCPCubicRoot(s);
        double t = r - sqrtf(disc);
        t = (t < 0) ? - FCPCubicRoot(-t) : FCPCubicRoot(t);
        
        double result = -term1 + s + t;
        if (result >= 0 && result <= 1) return result;
    } else if (disc == 0) {
    
    
        double r13 = (r < 0) ? - FCPCubicRoot(-r) : FCPCubicRoot(r);
        
        double result = -term1 + 2.0 * r13;
        if (result >= 0 && result <= 1) return result;
        
        result = -(r13 + term1);
        if (result >= 0 && result <= 1) return result;
    } else {
    
    
        q = -q;
        double dum1 = q * q * q;
        dum1 = acosf(r / sqrtf(dum1));
        double r13 = 2.0 * sqrtf(q);
        
        double result = -term1 + r13 * cos(dum1 / 3.0);
        if (result >= 0 && result <= 1) return result;
        
        result = -term1 + r13 * cos((dum1 + 2.0 * M_PI) / 3.0);
        if (result >= 0 && result <= 1) return result;
        
        result = -term1 + r13 * cos((dum1 + 4.0 * M_PI) / 3.0);
        if (result >= 0 && result <= 1) return result;
    }
    
    return -1;
}

上面代码中用到的知识：

• 一元三次方程判别式：

$$△=\frac{q^2}{4}+\frac{p^2}{27}$$

• 标准型方程中卡尔丹公式的一个实根：