【调制解调】AM 调幅

说明

学习数字信号处理算法时整理的学习笔记。同系列文章目录可见 《DSP 学习之路》目录，代码已上传到 Github - ModulationAndDemodulation。本篇介绍 AM 调幅信号的调制与解调，内附全套 MATLAB 代码。

1. AM 调制算法

1.1 算法描述

用调制信号去控制载波的幅度，使其按照调制信号的规律变化，当调制信号是模拟信号时，这个过程就被称为调幅（AM）。AM 信号的时域表达式为：
$$s_{AM}(t)=\left[A_0+m(t)\right]cos{\omega }_{c}t\text{\hspace{1em}(1)}$$

式中：$A_0$ 为外加的直流分量；$m(t)$ 是调制信号（携带要发出去的信息），它可以是确知信号，也可以是随机信号，其均值通常为 0；$cos{\omega }_{c}t$ 是载波，${\omega }_c$ 是载波角频率，与载波频率 $f_c$ 之间的关系为 ${\omega }_c=2\pi f_c$。

对式 $(1)$ 进行傅里叶变换，得到 AM 信号的频谱（幅度谱）表达式：
$$S_{AM}(\omega )=\pi A_0\left[\delta (\omega +{\omega }_c)+\delta (\omega -{\omega }_c)\right]+\frac{1}{2}\left[M(\omega +{\omega }_c)+M(\omega -{\omega }_c)\right]\text{\hspace{1em}(2)}$$
式中，$M(\omega )$ 是调制信号 $m(t)$ 的频谱。AM 信号的特性如下：

• $|m(t){|}_{max}$ 与 $A_0$ 的比值被称为调幅深度，或者调制指数，即 $\beta =|m(t){|}_{max}/A_0$，取值范围为 $(0,1]$，若调幅深度比 1 大，AM 信号的包络会出现严重失真，此时无法用包络检波法从 $s_{AM}(t)$ 中解调出 $m(t)$。在接收端估算调制指数时，可以先提取信号包络 $A(t)$，然后使用公式
  $$\hat{\beta }=\frac{A_{max}-A_{min}}{A_{max}+A_{min}}\text{\hspace{1em}(3)}$$
  对调制指数进行估算。

• AM 信号的频谱由载波分量、上边带、下边带三部分组成。上边带的频谱结构与原调制信号的频谱结构相同，下边带是上边带的镜像。因此，AM 信号是带有载波分量的双边带信号，它的带宽是基带信号（调制信号）带宽 $f_H$ 的 2 倍，即 $B_{AM}=2f_H$。

  

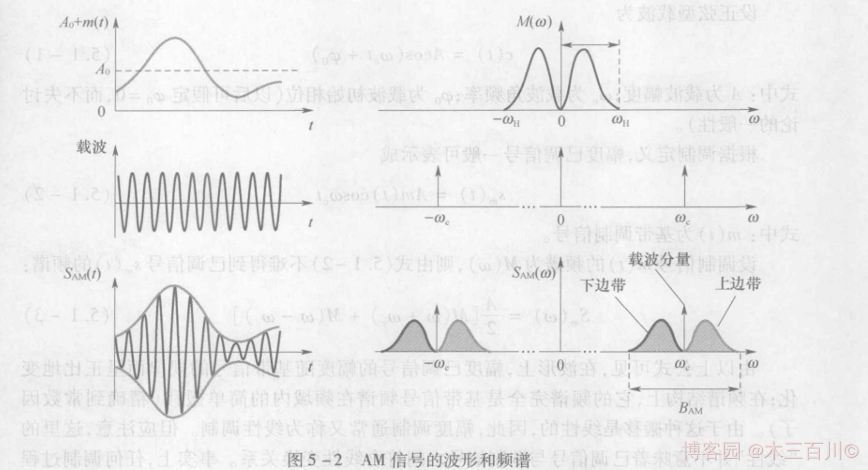
• 有用功率 $P_s$（用于传输有用信息的总边带功率）占信号总功率 $P_{AM}$ 的比例被称为调制效率，即
  $${\eta }_{AM}=\frac{P_s}{P_{AM}}=\frac{P_s}{P_c+P_s}=\frac{\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}\text{\hspace{1em}(4)}$$
  式中 $P_c$ 为载波功率，有 $P_c=A_0^2/2$，$P_s$ 为边带功率，有 $P_s=\overline{m^2(t)}/2$。当调制信号 $m(t)$ 为单频信号时，调制效率 ${\eta }_{AM}$ 与调制指数 ${\beta }_{AM}$ 存在如下关系：
  $${\eta }_{AM}=\frac{{\beta }_{AM}^2}{2+{\beta }_{AM}^2}\text{\hspace{1em}(5)}$$
  可得最大 AM 调制效率为 $1/3$，因此 AM 信号的功率利用率比较低。

1.2 调制信号 m(t) 为确知信号时

不妨假设确知信号 $m(t)$ 的时域表达式如下：
$$m(t)=sin(2\pi f_{m}t)+cos(\pi f_{m}t)\text{\hspace{1em}(6)}$$
各调制参数取值：$f_m=2500Hz$，$\beta =0.8$，$f_c=20000Hz$。信号采样率 $f_s=8f_c$，仿真总时长为 $2s$。AM 调制效果如下图所示（为了美观，时域只显示前 500 个点），调制信号 $m(t)$ 双边幅度谱有四根离散谱线（$\pm 2500Hz$、$\pm 1250Hz$），高频载波 $c(t)$ 双边幅度谱有两根离散谱线（$\pm 20000Hz$），AM 调幅信号 $s(t)$ 双边幅度谱有十根离散谱线（$\pm 22500Hz$、$\pm 21250Hz$、$\pm 20000Hz$、$\pm 18750Hz$、$\pm 17500Hz$）。

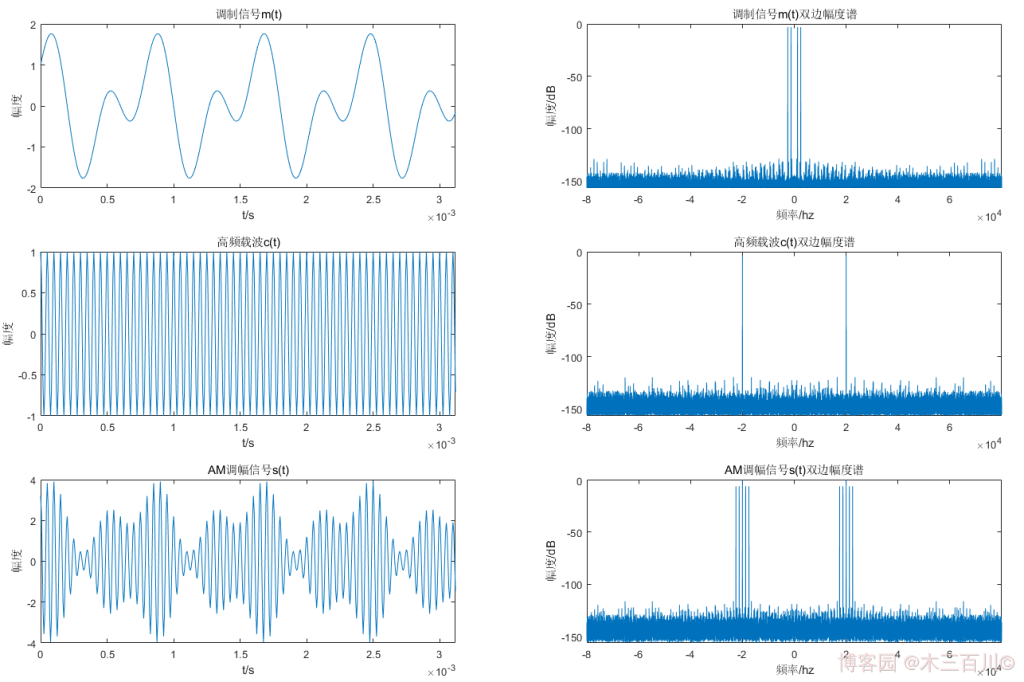
代码详见附录 main_modAM_example1.m 与 mod_am.m。

1.3 调制信号 m(t) 为随机信号时

不妨假设基带信号带宽为 $f_H=3000Hz$，各调制参数取值：$\beta =0.8$，$f_c=20000Hz$。信号采样率 $f_s=8f_c$，仿真总时长为 $2s$。AM 调制效果如下图所示（为了美观，时域只显示前 500 个点），调制信号 $m(t)$ 双边幅度谱中间谱峰的范围约为 $-3000Hz\sim 3000Hz$，高频载波 $c(t)$ 双边幅度谱有两根离散谱线（$\pm 20000Hz$），AM 调幅信号 $s(t)$ 双边幅度谱有两根离散谱线（$\pm 20000Hz$）及两个谱峰（范围约为 $-23000Hz\sim -17000Hz$、$17000Hz\sim 23000Hz$）。

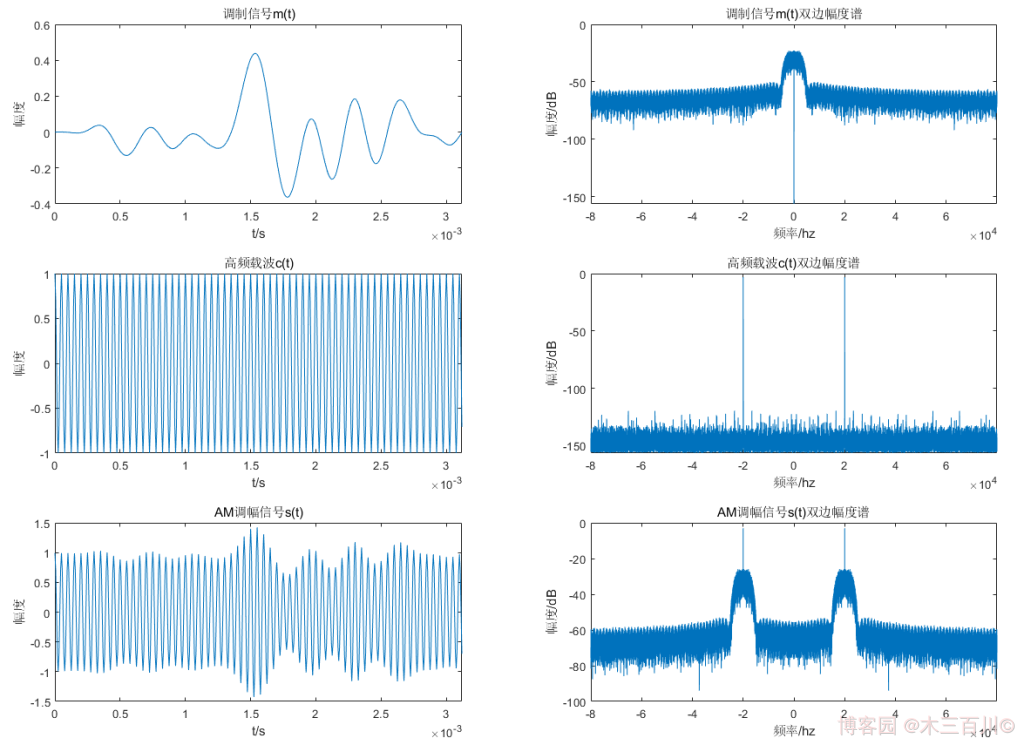
代码详见附录 main_modAM_example2.m 与 mod_am.m。

2. AM 解调算法

解调是调制的逆过程，其作用是从接收的已调信号中恢复原基带信号（即调制信号）。AM 解调的方法可分为两类：相干解调和非相干解调（包络检波），一般都采用包络检波。对上面 1.2 节中生成的 AM 信号加高斯白噪声，假设信噪比 $SNR=50dB$，加噪后的波形及频谱如下图所示（为了美观，时域只显示前 500 个点），频谱中有十根离散谱线（$\pm 22500Hz$、$\pm 21250Hz$、$\pm 20000Hz$、$\pm 18750Hz$、$\pm 17500Hz$）：

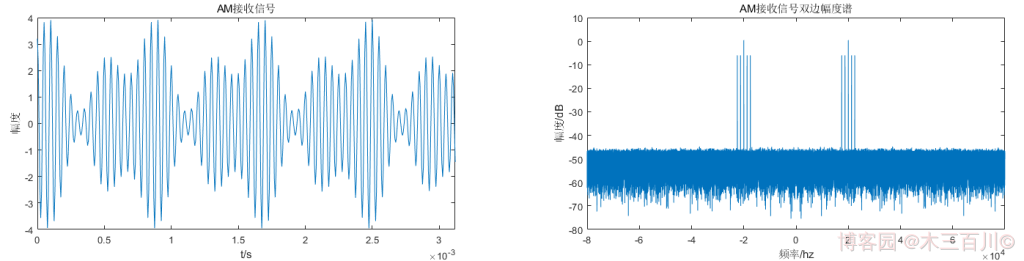
下面分别用几种不同方法对这个 AM 接收信号进行解调。

2.1 非相干解调（包络检波）

AM 信号在满足 $\beta \le 1$ 的条件下，其包络与调制信号 $m(t)$ 的形状完全一样，因此可以从信号包络中提取调制信号。AM 非相干解调（包络检波）一般有以下三个步骤：

1. 第一步：全波整流（对 $s(t)$ 取绝对值）或半波整流（将 $s(t)$ 小于 $0$ 的地方置零）。
2. 第二步：低通滤波器滤除高频载波，滤除 $2{\omega }_c$ 或 ${\omega }_c$。
3. 第三步：去除直流分量（减去自身均值）。

每一步结果的时域波形及频谱如下（为了美观，时域只显示前 500 个点）。全波整流结果的双边幅度谱中有二十根离散的谱线（$0Hz$、$\pm 1250Hz$、$\pm 2500Hz$、$\pm 37500Hz$、$\pm 38750Hz$、$\pm 40000Hz$、$\pm 41250Hz$、$\pm 42500Hz$、$\pm 77500Hz$、$\pm 78750Hz$、$-80000Hz$）。经过低通滤波后，只剩零频附近的五根谱线强度较大（$0Hz$、$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略。进一步去除直流后，只剩下调制信号中的四根谱线（$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略，此时的时域波形就是 AM 非相干解调的结果。

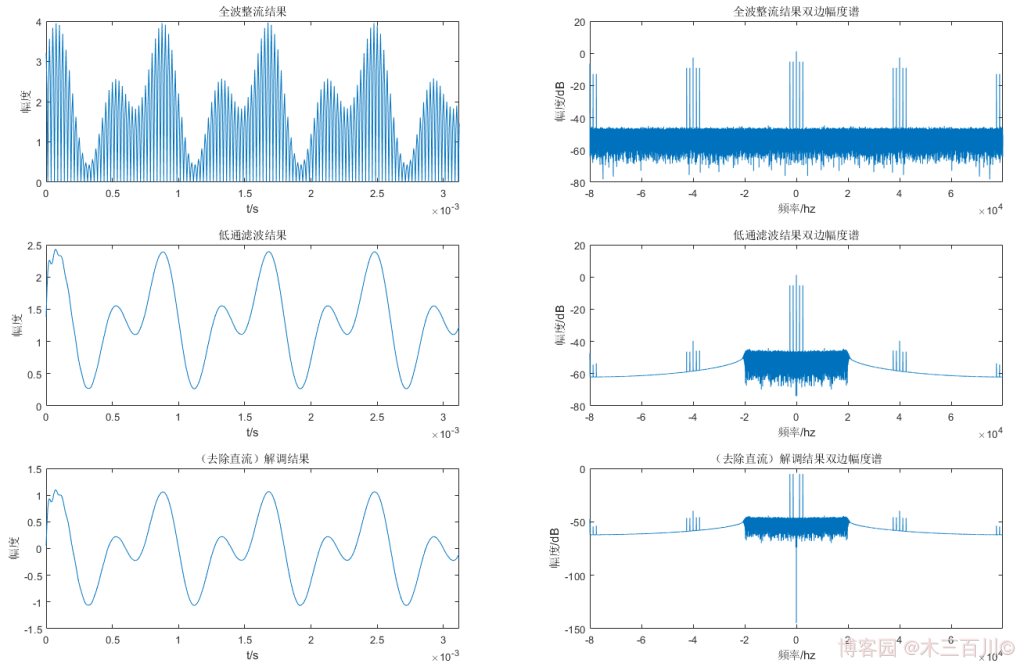
解调信号 $\hat{m}(t)$ 与调制信号 $m(t)$ 的对比效果如下：

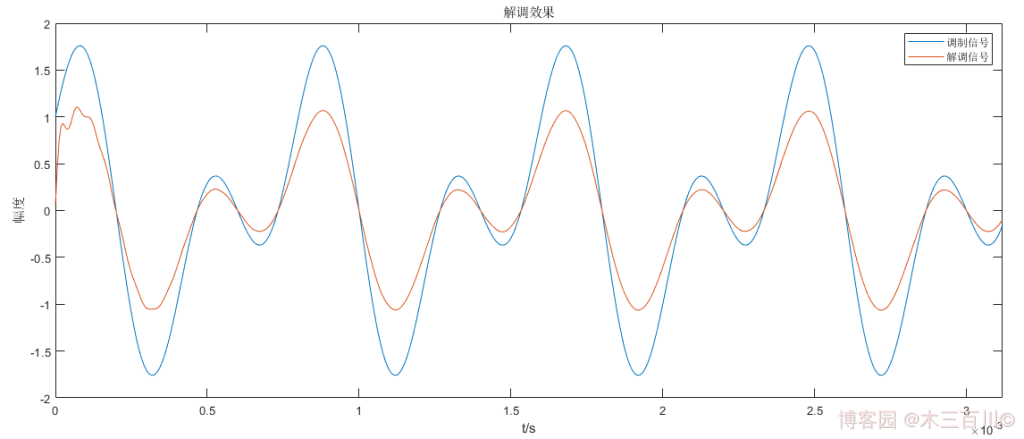
解调信号与调制信号波形基本一致，它们之间只相差一个比例系数，由 $k=\overline{|m(t)|}/\overline{|\hat{m}(t)|}$ 可计算出这个比例系数约为 $1.6567$，使用这个系数放大解调信号幅值，然后计算误差，有：$\sqrt{\sum |m(t_i)-k\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0054$。代码详见附录 main_demodAM_example1.m 与 demod_am_method1.m。

2.2 相干解调

相干解调时，为了无失真地恢复原基带信号，接收端必须提供一个与调制载波**严格同步（同频同相）**的本地载波（称为相干载波，可使用锁相环技术得到）。AM 相干解调一般有以下三个步骤：

1. 第一步：乘以相干载波（即乘以 $2cos({\omega }_{c}t+{\varphi }_0)$，前面的 2 被用来做幅度补偿，详见《通信原理》教材）。
2. 第二步：低通滤波器滤除高频载波，滤除 $2{\omega }_c$。
3. 第三步：去除直流分量（减去自身均值）。

解调时不妨取相干载波初相位为 ${\varphi }_0=0$，更靠谱点的需使用锁相环技术。每一步结果的时域波形及频谱如下（为了美观，时域只显示前 500 个点）。乘以相干载波结果的双边幅度谱中有十五根离散的谱线（$0Hz$、$\pm 1250Hz$、$\pm 2500Hz$、$\pm 37500Hz$、$\pm 38750Hz$、$\pm 40000Hz$、$\pm 41250Hz$、$\pm 42500Hz$）。经过低通滤波后，只剩零频附近的五根谱线强度较大（$0Hz$、$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略。进一步去除直流后，只剩下调制信号中的四根谱线（$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略，此时的时域波形就是 AM 相干解调的结果。

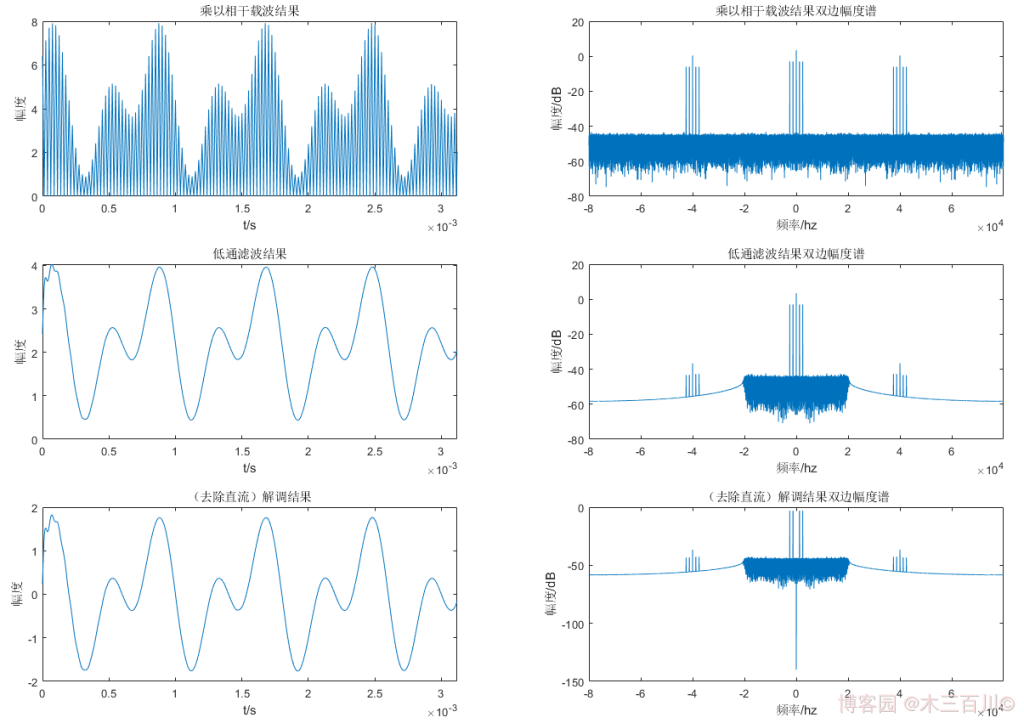
解调信号 $\hat{m}(t)$ 与调制信号 $m(t)$ 的对比效果如下：

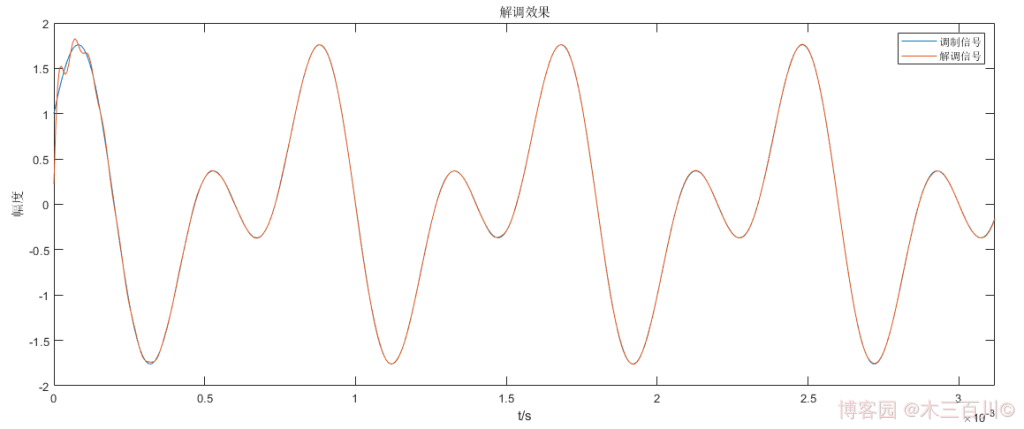
解调信号与调制信号波形基本重回，计算误差，有：$\sqrt{\sum |m(t_i)-\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0053$。更改相干载波的初始相位为 ${\varphi }_0=\pi /4,\pi /2$，或者更改相干载波的中心频率为 $0.8f_c,1.2f_c$ 后，解调效果变差，说明这种方法对相干载波同频同相的要求较高，鲁棒性不够强悍，可使用锁相环技术来改善这一缺点。代码详见附录 main_demodAM_example2.m 与 demod_am_method2.m。

2.3 数字正交解调

数字正交解调也属于相干解调的一种，但这种方法具有较强的抗载频失配能力，不要求相干载波严格的同频同相。AM 数字正交解调一般有以下四个步骤：

1. 第一步：乘以正交相干载波得到 $s_I(t)$ 与 $s_Q(t)$，即 $s_I(t)=2s(t)cos({\omega }_{c}t+{\varphi }_0)$，$s_Q(t)=-2s(t)sin({\omega }_{c}t+{\varphi }_0)$，前面的 2 被用来做幅度补偿。
2. 第二步：低通滤波器滤除 $s_I(t)$ 与 $s_Q(t)$ 中的高频分量。
3. 第三步：计算包络 $A(t)=\sqrt{s_I^2(t)+s_Q^2(t)}$。
4. 第四步：去除直流分量（减去自身均值）。

解调时不妨取相干载波初相位为 ${\varphi }_0=0$。第一步结果的时域波形及频谱如下（为了美观，时域只显示前 500 个点）。乘以正交相干载波后，$I$ 路双边幅度谱中有十五根离散谱线（$0Hz$、$\pm 1250Hz$、$\pm 2500Hz$、$\pm 37500Hz$、$\pm 38750Hz$、$\pm 40000Hz$、$\pm 41250Hz$、$\pm 42500Hz$），$Q$ 路双边幅度谱中有十根离散谱线（$\pm 37500Hz$、$\pm 38750Hz$、$\pm 40000Hz$、$\pm 41250Hz$、$\pm 42500Hz$）。

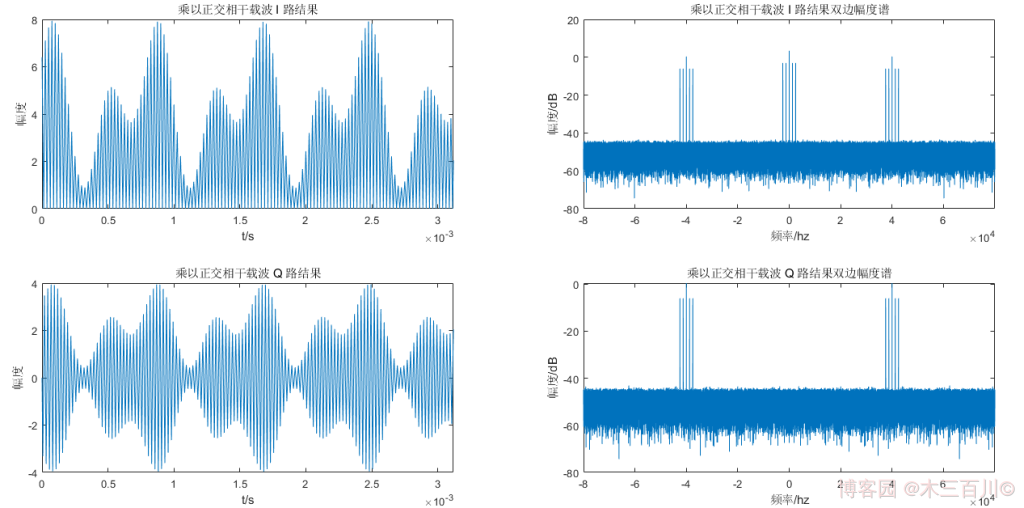
第二步结果的时域波形及频谱如下（为了美观，时域只显示前 500 个点）。经过低通滤波后，$I$ 路双边幅度谱只剩零频附近的五根谱线强度较大（$0Hz$、$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略，$Q$ 路双边幅度谱各谱线相对于 $I$ 路而言都可忽略。

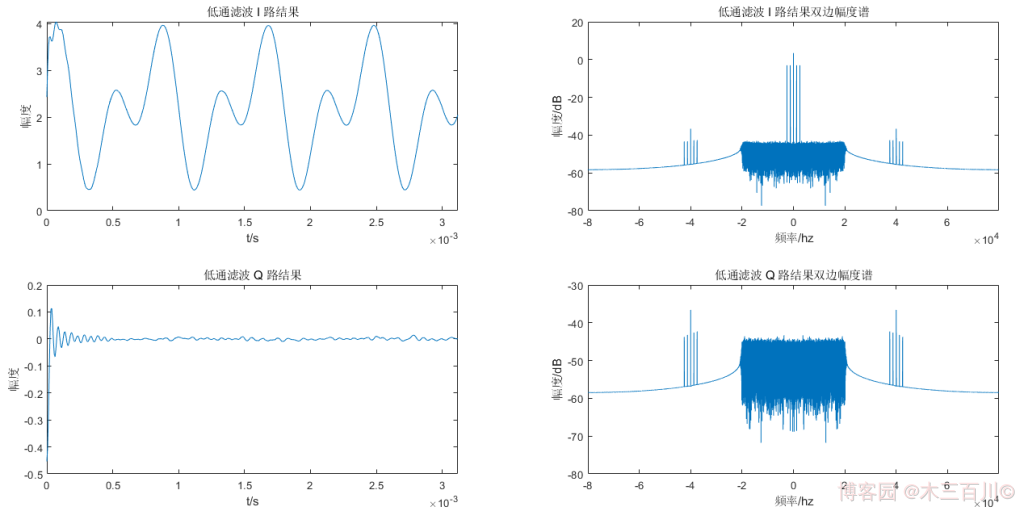
第三步以及第四步的时域波形及频谱如下（为了美观，时域只显示前 500 个点）。计算所得包络的双边幅度谱中，只剩零频附近的五根谱线强度较大（$0Hz$、$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略，进一步去除直流后，只剩下调制信号中的四根谱线（$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略，此时的时域波形就是 AM 相干解调的结果。

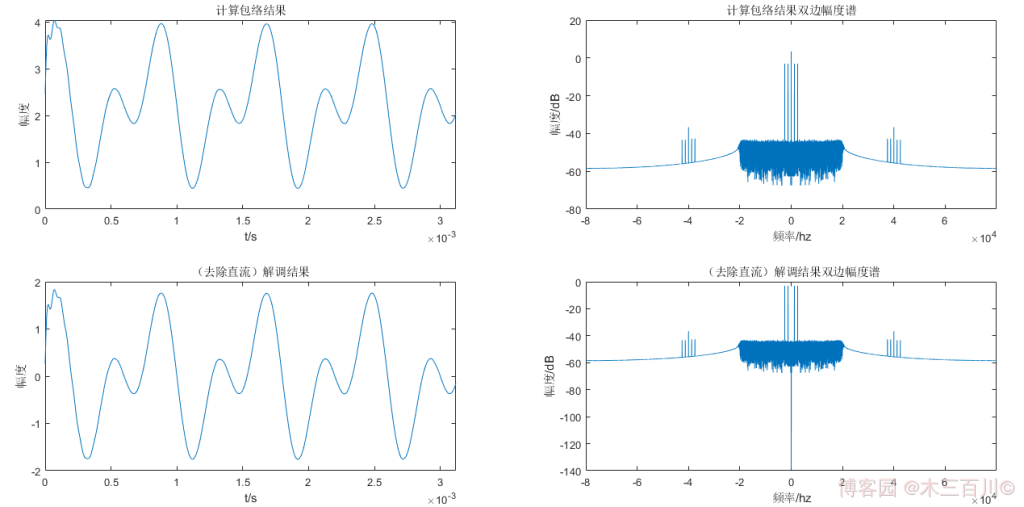
解调信号 $\hat{m}(t)$ 与调制信号 $m(t)$ 的对比效果如下：

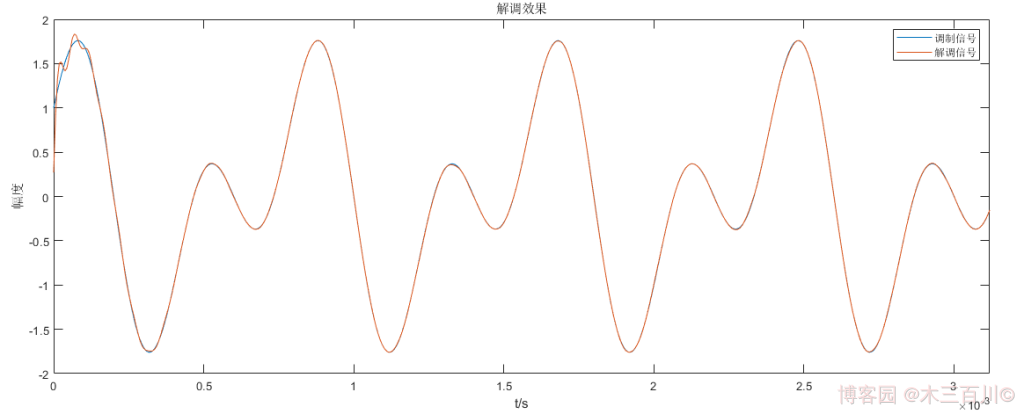
解调信号与调制信号波形基本重回，计算误差，有：$\sqrt{\sum |m(t_i)-\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0053$。更改相干载波的初始相位为 ${\varphi }_0=\pi /4,\pi /2$，或者更改相干载波的中心频率为 $0.8f_c,1.2f_c$ 后，解调效果依然很好，说明这种方法具有较好的抗载频失配能力。代码详见附录 main_demodAM_example3.m 与 demod_am_method3.m。

2.4 非相干解调（包络检波 - 希尔伯特变换法）

根据信号的希尔伯特变换，可以计算出 AM 信号的包络，这种方法用 MATLAB 实现极为简单，解调时无需任何载频信息：

1. 第一步：计算 AM 信号的希尔伯特变换，得到一个复信号（实部为原 AM 信号，虚部为其希尔伯特变换结果），对所得复信号取模，即为 AM 信号的包络。

2. 第二步：去除直流分量（减去自身均值）。

每一步结果的时域波形及频谱如下（为了美观，时域只显示前 500 个点）。希尔伯特变换所得包络的双边幅度谱中有五根离散的谱线（$0Hz$、$\pm 1250Hz$、$\pm 2500Hz$）。去除直流后，只剩下调制信号中的四根谱线（$\pm 2500Hz$、$\pm 1250Hz$），剩余谱线可忽略，此时的时域波形就是 AM 非相干解调的结果。

解调信号 $\hat{m}(t)$ 与调制信号 $m(t)$ 的对比效果如下：

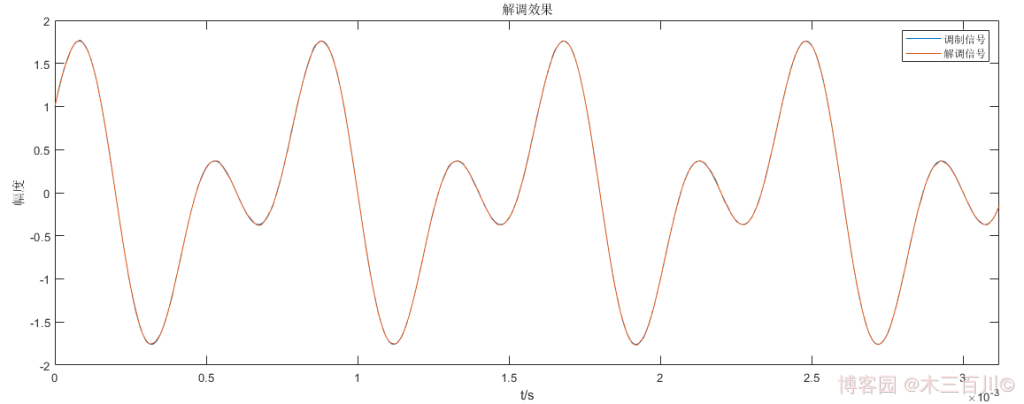
解调信号与调制信号波形基本重回，计算误差，有：$\sqrt{\sum |m(t_i)-\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0054$。代码详见附录 main_demodAM_example4.m 与 demod_am_method4.m。

3. AM 仿真（MATLAB Communications Toolbox）

MATLAB 的 Communications Toolbox 中提供了 AM 调制函数 ammod，高斯白噪声函数 awgn，以及 AM 解调函数 amdemod，可以很方便地完成 AM 信号仿真。使用这三个函数实现上面 1.2 节中确知信号 $m(t)$ 的 AM 调制解调，调制后加噪声的效果如下：

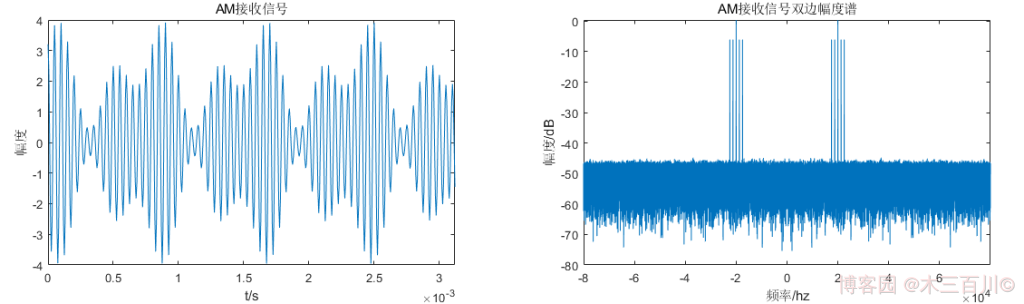
解调效果如下：

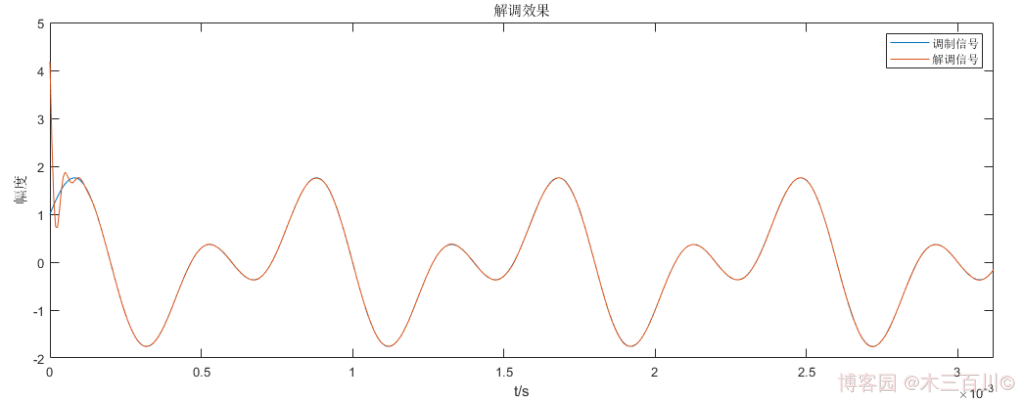
解调信号与调制信号波形基本重回，计算误差，有：$\sqrt{\sum |m(t_i)-\hat{m}(t_i){|}^2}/\sqrt{\sum |m(t_i){|}^2}\approx 0.0074$。代码详见附录 main_CommAM_example.m。

参考资料

[1] 楼才义,徐建良,杨小牛.软件无线电原理与应用[M].电子工业出版社,2014.

[2] 樊昌信,曹丽娜.通信原理.第7版[M].国防工业出版社,2012.

[3] CSDN - 幅度调制AM。

[4] 知乎 - 什么是AM波的调制指数和传输效率？。

附录代码

附.1 文件 mod_am.m

function [ sig_am ] = mod_am(fc, beta, fs, mt, t)
% MOD_AM        AM 调幅
% 输入参数：
%       fc      载波中心频率
%       beta    调幅深度/调制指数
%       fs      信号采样率
%       mt      调制信号
%       t       采样时间
% 输出参数：
%       sig_am  调幅(AM)实信号
% @author 木三百川

% 计算直流分量
A0 = max(abs(mt))/beta;

% 生成信号
ct = cos(2*pi*fc*t);      % 载波信号
sig_am = (A0+mt).*ct;     % AM调幅信号

% 绘图
nfft = length(sig_am);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am));
subplot(3,2,1);
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('调制信号m(t)');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(mt,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('调制信号m(t)双边幅度谱');

subplot(3,2,3);
plot(t(1:plot_length), ct(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('高频载波c(t)');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(ct,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('高频载波c(t)双边幅度谱');

subplot(3,2,5);
plot(t(1:plot_length), sig_am(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('AM调幅信号s(t)');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_am,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('AM调幅信号s(t)双边幅度谱');

end

附.2 文件 main_modAM_example1.m

clc;
clear;
close all;
% AM 调制仿真(调制信号为确知信号)
% @author 木三百川

% 调制参数
fm = 2500;              % 调制信号参数
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% AM 调制
[ sig_am ] = mod_am(fc, beta, fs, mt, t);

附.3 文件 main_modAM_example2.m

clc;
clear;
close all;
% AM 调制仿真(调制信号为随机信号)
% @author 木三百川

% 调制参数
fH = 3000;          	% 基带信号带宽
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为随机信号
mt = randn(size(t));
b = fir1(512, fH/(fs/2), 'low');
mt = filter(b,1,mt);
mt = mt - mean(mt);

% AM 调制
[ sig_am ] = mod_am(fc, beta, fs, mt, t);

附.4 文件 demod_am_method1.m

function [ sig_am_demod ] = demod_am_method1(sig_am_receive, fc, fs, t)
% DEMOD_AM_METHOD1        AM 非相干解调（包络检波）
% 输入参数：
%       sig_am_receive      AM 接收信号，行向量
%       fc                  载波中心频率
%       fs                  信号采样率
%       t                   采样时间
% 输出参数：
%       sig_am_demod        解调结果，与 sig_am_receive 等长
% @author 木三百川

% 第一步：全波整流
sig_am_abs = abs(sig_am_receive);

% 第二步：低通滤波(补零进行时延修正)
b = fir1(256, fc/(fs/2), 'low');
sig_am_lpf = filter(b,1,[sig_am_abs,zeros(1, fix(length(b)/2))]);
sig_am_lpf = sig_am_lpf(fix(length(b)/2)+1:end);

% 第三步：去除直流分量
sig_am_demod = sig_am_lpf - mean(sig_am_lpf);

% 绘图
nfft = length(sig_am_abs);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_abs));
subplot(3,2,1);
plot(t(1:plot_length), sig_am_abs(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('全波整流结果');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_abs,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('全波整流结果双边幅度谱');

subplot(3,2,3);
plot(t(1:plot_length), sig_am_lpf(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('低通滤波结果');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_lpf,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('低通滤波结果双边幅度谱');

subplot(3,2,5);
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('（去除直流）解调结果');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_demod,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('（去除直流）解调结果双边幅度谱');

end

附.5 文件 main_demodAM_example1.m

clc;
clear;
close all;
% AM 解调仿真(调制信号为确知信号，非相干解调/包络检波)
% @author 木三百川

% 调制参数
fm = 2500;              % 调制信号参数
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% AM 调制
[ sig_am_send ] = mod_am(fc, beta, fs, mt, t);

% 加噪声
snr = 50;               % 信噪比
sig_am_receive = awgn(sig_am_send, snr, 'measured');

% 非相干解调
[ sig_am_demod ] = demod_am_method1(sig_am_receive, fc, fs, t);

% 绘图
nfft = length(sig_am_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_am_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('AM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('AM接收信号双边幅度谱');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号');

coef = mean(abs(mt))/mean(abs(sig_am_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_am_demod)/norm(mt));

附.6 文件 demod_am_method2.m

function [ sig_am_demod ] = demod_am_method2(sig_am_receive, fc, fs, t, phi0)
% DEMOD_AM_METHOD2        AM 相干解调
% 输入参数：
%       sig_am_receive      AM 接收信号，行向量
%       fc                  载波中心频率
%       fs                  信号采样率
%       t                   采样时间
%       phi0                相干载波初始相位
% 输出参数：
%       sig_am_demod        解调结果，与 sig_am_receive 等长
% @author 木三百川

% 第一步：乘以相干载波
ct = 2*cos(2*pi*fc*t+phi0);
sig_am_ct = sig_am_receive.*ct;

% 第二步：低通滤波(补零进行时延修正)
b = fir1(256, fc/(fs/2), 'low');
sig_am_lpf = filter(b,1,[sig_am_ct,zeros(1, fix(length(b)/2))]);
sig_am_lpf = sig_am_lpf(fix(length(b)/2)+1:end);

% 第三步：去除直流分量
sig_am_demod = sig_am_lpf - mean(sig_am_lpf);

% 绘图
nfft = length(sig_am_ct);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_ct));
subplot(3,2,1);
plot(t(1:plot_length), sig_am_ct(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('乘以相干载波结果');
subplot(3,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_ct,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('乘以相干载波结果双边幅度谱');

subplot(3,2,3);
plot(t(1:plot_length), sig_am_lpf(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('低通滤波结果');
subplot(3,2,4);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_lpf,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('低通滤波结果双边幅度谱');

subplot(3,2,5);
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('（去除直流）解调结果');
subplot(3,2,6);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_demod,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('（去除直流）解调结果双边幅度谱');

end

附.7 文件 main_demodAM_example2.m

clc;
clear;
close all;
% AM 解调仿真(调制信号为确知信号，相干解调)
% @author 木三百川

% 调制参数
fm = 2500;              % 调制信号参数
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% AM 调制
[ sig_am_send ] = mod_am(fc, beta, fs, mt, t);

% 加噪声
snr = 50;               % 信噪比
sig_am_receive = awgn(sig_am_send, snr, 'measured');

% 非相干解调
phi0 = 0;               % 相干载波初相位
[ sig_am_demod ] = demod_am_method2(sig_am_receive, fc, fs, t, phi0);

% 绘图
nfft = length(sig_am_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_am_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('AM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('AM接收信号双边幅度谱');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号');

coef = mean(abs(mt))/mean(abs(sig_am_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_am_demod)/norm(mt));

附.8 文件 demod_am_method3.m

function [ sig_am_demod ] = demod_am_method3(sig_am_receive, fc, fs, t, phi0)
% DEMOD_AM_METHOD3        AM 数字正交解调/相干解调
% 输入参数：
%       sig_am_receive      AM 接收信号，行向量
%       fc                  载波中心频率
%       fs                  信号采样率
%       t                   采样时间
%       phi0                相干载波初始相位
% 输出参数：
%       sig_am_demod        解调结果，与 sig_am_receive 等长
% @author 木三百川

% 第一步：乘以正交相干载波
sig_am_i = 2*sig_am_receive.*cos(2*pi*fc*t+phi0);
sig_am_q = -2*sig_am_receive.*sin(2*pi*fc*t+phi0);

% 第二步：低通滤波(补零进行时延修正)
b = fir1(256, fc/(fs/2), 'low');
sig_am_i_lpf = filter(b,1,[sig_am_i,zeros(1,fix(length(b)/2))]);
sig_am_q_lpf = filter(b,1,[sig_am_q,zeros(1,fix(length(b)/2))]);
sig_am_i_lpf = sig_am_i_lpf(fix(length(b)/2)+1:end);
sig_am_q_lpf = sig_am_q_lpf(fix(length(b)/2)+1:end);

% 第三步：计算包络
At = sqrt(sig_am_i_lpf.^2 + sig_am_q_lpf.^2);

% 第四步：去除直流分量
sig_am_demod = At - mean(At);

% 绘图
nfft = length(sig_am_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_receive));
subplot(2,2,1);
plot(t(1:plot_length), sig_am_i(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('乘以正交相干载波 I 路结果');
subplot(2,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_i,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('乘以正交相干载波 I 路结果双边幅度谱');
subplot(2,2,3);
plot(t(1:plot_length), sig_am_q(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('乘以正交相干载波 Q 路结果');
subplot(2,2,4);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_q,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('乘以正交相干载波 Q 路结果双边幅度谱');

figure;set(gcf,'color','w');
subplot(2,2,1);
plot(t(1:plot_length), sig_am_i_lpf(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('低通滤波 I 路结果');
subplot(2,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_i_lpf,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('低通滤波 I 路结果双边幅度谱');
subplot(2,2,3);
plot(t(1:plot_length), sig_am_q_lpf(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('低通滤波 Q 路结果');
subplot(2,2,4);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_q_lpf,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('低通滤波 Q 路结果双边幅度谱');

figure;set(gcf,'color','w');
subplot(2,2,1);
plot(t(1:plot_length), At(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('计算包络结果');
subplot(2,2,2);
plot(freq, 10*log10(fftshift(abs(fft(At,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('计算包络结果双边幅度谱');
subplot(2,2,3);
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('（去除直流）解调结果');
subplot(2,2,4);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_demod,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('（去除直流）解调结果双边幅度谱');

end

附.9 文件 main_demodAM_example3.m

clc;
clear;
close all;
% AM 解调仿真(调制信号为确知信号，数字正交解调/相干解调)
% @author 木三百川

% 调制参数
fm = 2500;              % 调制信号参数
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% AM 调制
[ sig_am_send ] = mod_am(fc, beta, fs, mt, t);

% 加噪声
snr = 50;               % 信噪比
sig_am_receive = awgn(sig_am_send, snr, 'measured');

% 非相干解调
phi0 = 0;               % 相干载波初相位
[ sig_am_demod ] = demod_am_method3(sig_am_receive, fc, fs, t, phi0);

% 绘图
nfft = length(sig_am_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_am_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('AM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('AM接收信号双边幅度谱');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号');

coef = mean(abs(mt))/mean(abs(sig_am_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_am_demod)/norm(mt));

附.10 文件 demod_am_method4.m

function [ sig_am_demod ] = demod_am_method4(sig_am_receive, fs, t)
% DEMOD_AM_METHOD1        AM 非相干解调（包络检波，Hilbert变换计算包络）
% 输入参数：
%       sig_am_receive      AM 接收信号，行向量
%       fs                  信号采样率
%       t                   采样时间
% 输出参数：
%       sig_am_demod        解调结果，与 sig_am_receive 等长
% @author 木三百川

% 第一步：计算信号包络
sig_am_envelope = abs(hilbert(sig_am_receive));

% 第二步：去除直流分量
sig_am_demod = sig_am_envelope - mean(sig_am_envelope);

% 绘图
nfft = length(sig_am_envelope);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_envelope));
subplot(2,2,1);
plot(t(1:plot_length), sig_am_envelope(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('Hilbert变换计算包络结果');
subplot(2,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_envelope,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('Hilbert变换计算包络结果双边幅度谱');
subplot(2,2,3);
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('（去除直流）解调结果');
subplot(2,2,4);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_demod,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('（去除直流）解调结果双边幅度谱');

end

附.11 文件 main_demodAM_example4.m

clc;
clear;
close all;
% AM 解调仿真(调制信号为确知信号，非相干解调，包络检波，Hilbert变换计算包络)
% @author 木三百川

% 调制参数
fm = 2500;              % 调制信号参数
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% AM 调制
[ sig_am_send ] = mod_am(fc, beta, fs, mt, t);

% 加噪声
snr = 50;               % 信噪比
sig_am_receive = awgn(sig_am_send, snr, 'measured');

% 非相干解调
[ sig_am_demod ] = demod_am_method4(sig_am_receive, fs, t);

% 绘图
nfft = length(sig_am_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_am_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('AM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('AM接收信号双边幅度谱');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号');

coef = mean(abs(mt))/mean(abs(sig_am_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_am_demod)/norm(mt));

附.12 文件 main_CommAM_example.m

clc;
clear;
close all;
% AM 调制解调仿真(使用Communications Toolbox工具箱)
% @author 木三百川

% 调制参数
fm = 2500;              % 调制信号参数
beta = 0.8;             % 调幅深度/调制指数
fc = 20000;             % 载波频率
fs = 8*fc;              % 采样率
total_time = 2;         % 仿真时长，单位：秒

% 采样时间
t = 0:1/fs:total_time-1/fs;

% 调制信号为确知信号
mt = sin(2*pi*fm*t)+cos(pi*fm*t);

% AM 调制
A0 = max(abs(mt))/beta;
ini_phase = 0;
sig_am_send = ammod(mt, fc, fs, ini_phase, A0);

% 加噪声
snr = 50;               % 信噪比
sig_am_receive = awgn(sig_am_send, snr, 'measured');

% AM 解调
[ sig_am_demod ] = amdemod(sig_am_receive, fc, fs, ini_phase, A0);

% 绘图
nfft = length(sig_am_receive);
freq = (-nfft/2:nfft/2-1).'*(fs/nfft);
figure;set(gcf,'color','w');
plot_length = min(500, length(sig_am_receive));
subplot(1,2,1);
plot(t(1:plot_length), sig_am_receive(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('AM接收信号');
subplot(1,2,2);
plot(freq, 10*log10(fftshift(abs(fft(sig_am_receive,nfft)/nfft))+eps));xlim([freq(1),freq(end)]);
xlabel('频率/hz');ylabel('幅度/dB');title('AM接收信号双边幅度谱');

figure;set(gcf,'color','w');
plot(t(1:plot_length), mt(1:plot_length));xlim([t(1),t(plot_length)]);
hold on;
plot(t(1:plot_length), sig_am_demod(1:plot_length));xlim([t(1),t(plot_length)]);
xlabel('t/s');ylabel('幅度');title('解调效果');
legend('调制信号','解调信号');

coef = mean(abs(mt))/mean(abs(sig_am_demod));
fprintf('norm(调制信号 - %.2f * 解调信号)/norm(调制信号) = %.4f.\n', coef, norm(mt-coef*sig_am_demod)/norm(mt));