通常情况下，我们对下游资源（如db）的保护，是通过对上游接口限流进行的；多个接口的峰值时间点按约定错峰，并给予一定流量限制，可以保护下游资源在安全水位内。
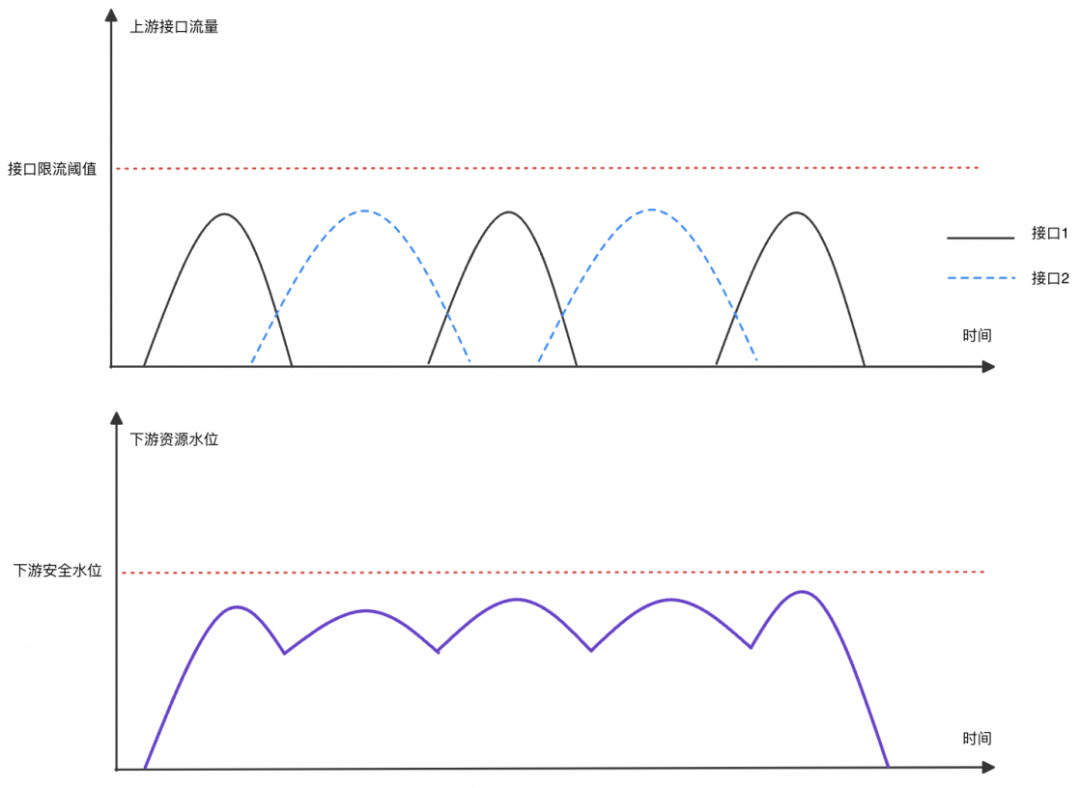
这种做法有以下缺点：
随着业务迭代，上游接口接入方越来越多，形形色色的接口也越开越多，这就导致上游接口的峰值时间错中复杂，难以评估；
上游接口的峰值时间有时候是由口头/书面约定而成，没有强制的系统制约，这就导致多个接口峰值可能会出现如下叠加情况，最终让下游资源水位超过安全阈值。
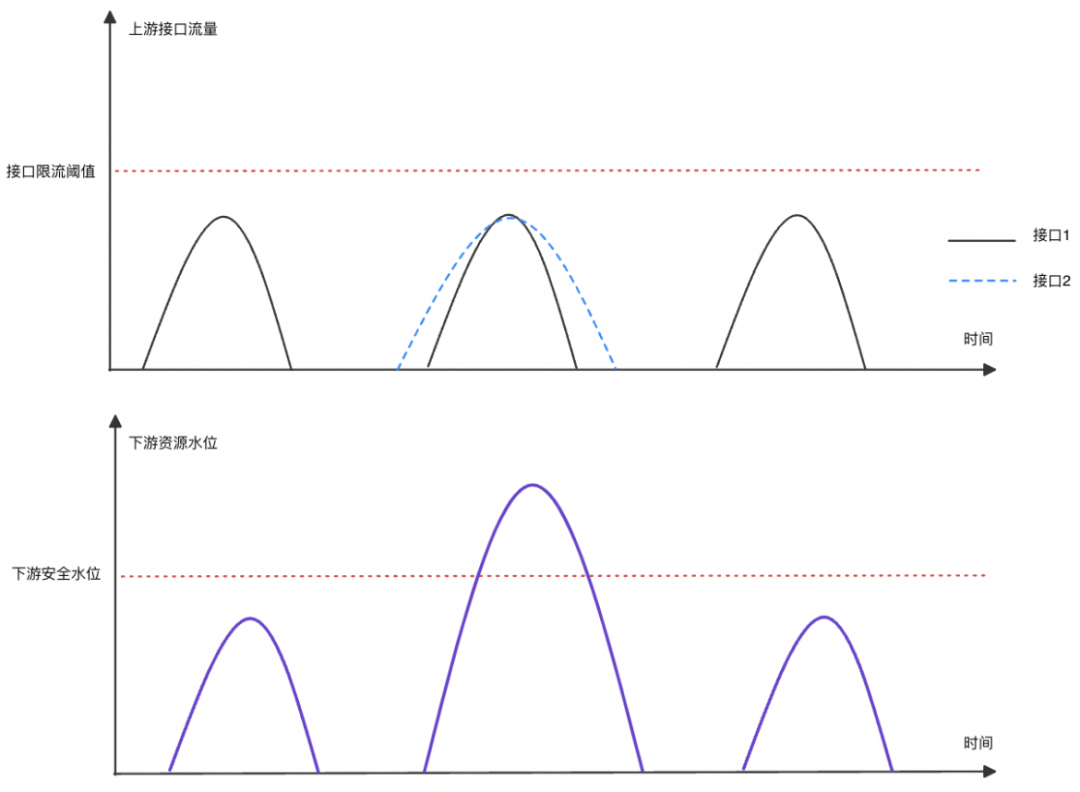
为了避免问题2的出现，多数系统的做法是将上游接口的限流阈值设置得更低或是对下游资源进行扩容，来保障下游水位安全；但是这种做法又会导致下游长期的资源浪费。
所以，本文实现了一种限流工具，能够基于下游资源的水位自适应调节上游接口流量；即保护的是下游资源水位，但是保护的方式是调节影响该资源的上游接口流量。
介绍
KLimiter为了实现上述诉求，并且支持不同入口优先级不同，本文的限流工具有如下能力：
秒级监测多个下游资源的水位；
自适应调节多个入口的流量，将下游资源水位维持在阈值之下；
多个入口可设置不同的优先级，优先降低低优先级的入口流量到一定比例。
概要设计
▐ 限流方案
基于流量比例进行限流，比如另入口流量比例为70%，那么将阻断30%的请求。
▐ 名词解释
名词 |
解释 |
例子 |
限流入口 |
需要限制流量的入口 |
如【查询xxx的接口】就是一个限流入口 |
资源基线 |
自适应限流需要关注的下游资源实例；基线包含名称和其水位值 |
如【 xx库】就是一个资源基线，本文用xx库的操作qps来描述其水位值 |
入口影响的基线 |
限流入口会影响资源基线 |
如【xx接口】，会影响到【aa库】【bb库】这两个基线的水位 |
影响系数 |
一个基线可能由多个限流入口影响，不同的入口在不同的时刻，对基线影响的占比是不一样的，这个占比进行归一化后叫做影响系数 |
如【 aa库】会由【xx接口】、【yy接口】等多个入口影响，某个时刻，一次【xx接口】请求对【 aa库】贡献1qps，一次【yy接口】请求对【 aa库】贡献3qps，则【xx接口】影响系数为0.25，【yy接口】影响系数为0.75；这个影响系数在按优先级调流时会用到 |
流量比例 |
本文通过限制入口的流量比例来实现限流，而不是限制一个具体的qps值 |
|
入口优先级 |
本文入口优先级，定义为期望该入口最多能降低到的流量比例 |
▐ 设计图解
-
调流原理
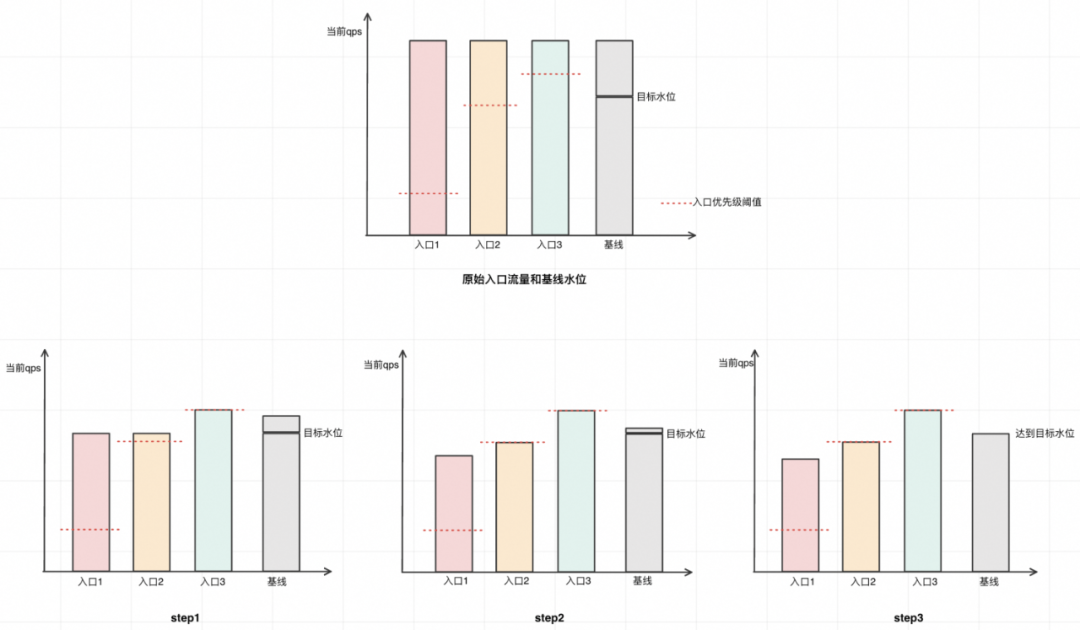
如图，本文自适应限流器会优先保证入口流量高于其设置的优先级阈值，如果该入口不能再降低流量了，会先降低其他优先级更低的入口流量。如step1中，入口3的流量比例降低到优先级阈值就不能再降了，在step2会让入口1和入口2去降低原本应该由入口3降低的流量比例。
如果所有入口的流量比例均到了优先级的阈值：
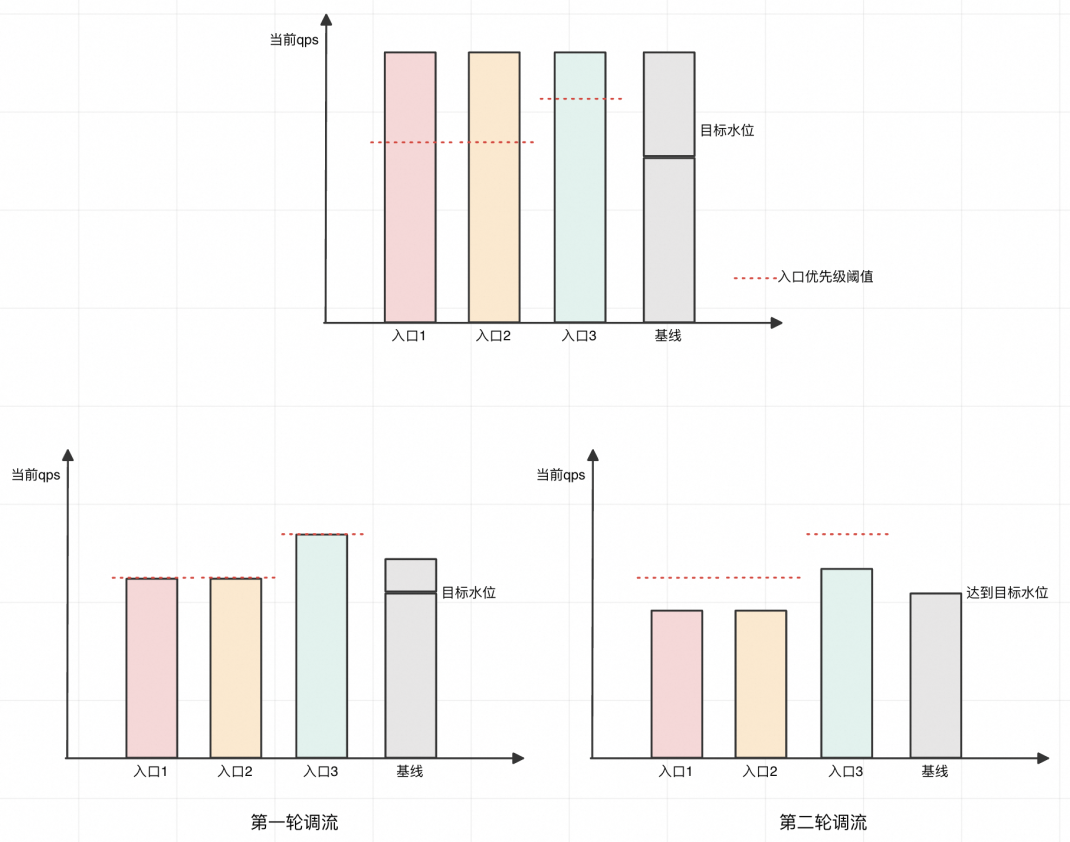
则会进行第二轮调流，第二轮会一视同仁，所有入口一起降。
-
代码模块
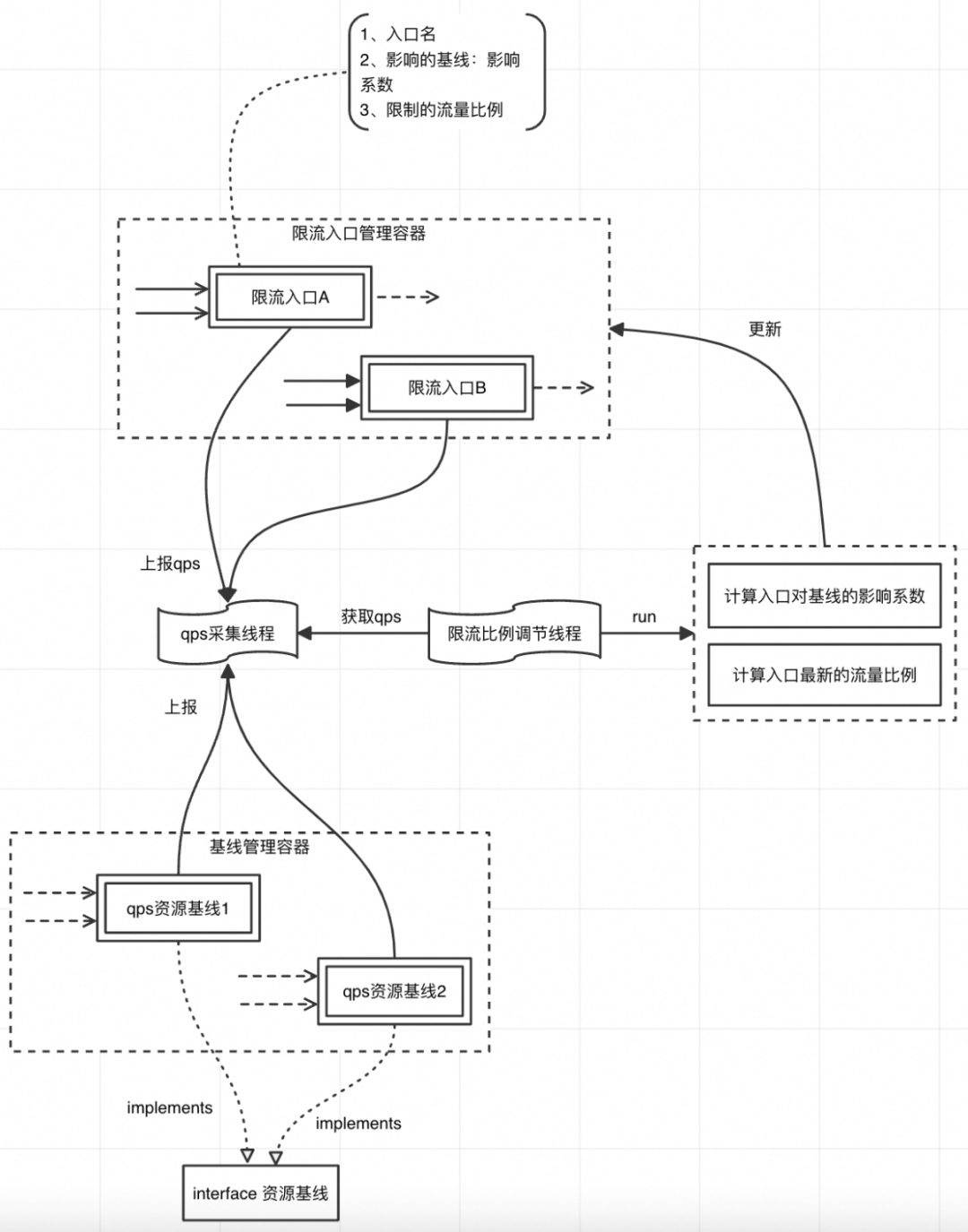
如图，一个限流入口会影响多个资源基线，一个资源基线也会被多个限流入口影响；自适应限流器有2个后台线程，分别用于统计qps和计算入口的流量比例：
qps采集线程：每1s执行一次，遍历所有入口和基线，计算过去1s的qps值；
流量比例调节线程：每5s执行一次，基于6.1算法重新计算所有入口的影响系数，基于6.2、6.3算法重新计算所有入口的流量比例。
挑战
1、多个入口需要有限流的优先级，比如入口A最多降到90%流量比例，入口B最多降到70%流量比例，入口C可以降到0；假设基线期望降低10%的流量，理论上A、B、C均降低10%即可，但如果A流量比例已经是90%了，那么原本应该由A降低的这部分流量，需要由其它入口承担降低（其它入口要降低更多的流量），那么其他入口需要降低多少流量呢，这个比例需要怎么折算？
2、要解决1，需要引入影响系数，不同的入口对基线的影响系数是不一样的，假设A系数是0.4，B系数是0.3，C系数是0.3，那么B、C在降低了原本应该降低的10%流量后，基线还需要降低0.4 * 10%的水位；但是不同时间、不同入口的影响系数必然是在变化的，这个系数如何计算呢？
3、影响系数确定后，基线需要降低的流量比例确认后，多个入口在优先级的限制下，最终每个入口需要降低多少流量比例，这个如何计算呢？
本文设计核心即解决以上三个挑战。
▐ 限流入口系数求解
对于某个资源基线，我们以如下流程计算其入口在该资源基线下的影响系数。
假设有n个入口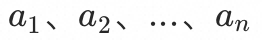
，共同影响资源基线y，我们可以知道这n个入口的qps
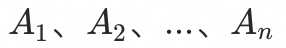，以及这个资源基线的水位L，就可以得出以下方程：
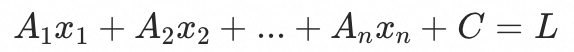
由于入口流量都为0的时候，基线水位L也为0，所以 C=0，即得到：
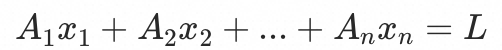
其中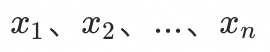
为n个入口的影响系数；可见，要得到这n个影响系数，需要n个这样的方程；
基于历史采样信息，我们可以获得过去的n个时刻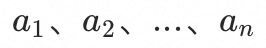
的qps矩阵：
令影响系数为：
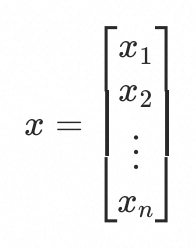
令历史n个时刻的基线水位为：
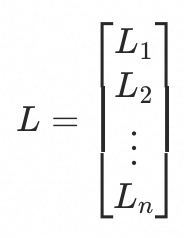
最终可以得到历史n个时刻的入口qps和水位关系的方程组：
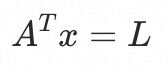
其为n元1次方程组，基于LU分解法（高斯消元法复杂度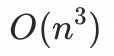
，LU分解法复杂度
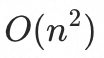, 故选择LU分解法求解）即可求出
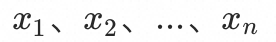，最终对它们进行归一化，这里的归一化并非向量的归一化，而是最终描述各个入口占所有入口对基线的影响比例：
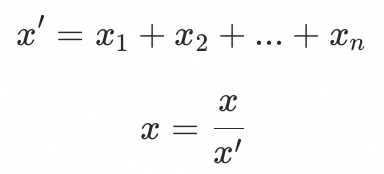
上述方法即可得出最终的影响系数；
由于LU分解本质是高斯消元法，需要矩阵A正定，否则无解；另外为负数的解也是没有实际意义的，所以需要讨论劣化场景。
当矩阵非正定，或求出的解为负数时，方程是无解或解是无意义的，此时可以将问题转换为优化问题，令
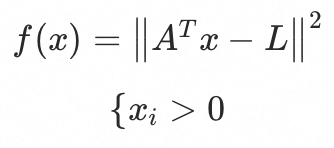
由于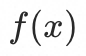
是单调的，所以可以用牛顿迭代法（Newton-Raphson）求最接近初始值近似，第k次迭代结果为：
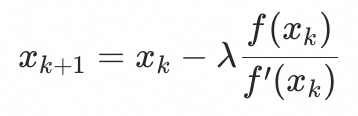
这里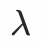
用于控制
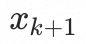均大于0，若无法满足，则停止迭代；
迭代初始值的选取为上一轮流量调控计算的系数结果，即让本次优化结果更接近于上一轮计算值。为了减少0值的影响，上一轮计算结果为0的，本轮初始值赋1。
▐ 流量降低算法
本文对入口定义的优先级，为期望该入口最多能降低到的流量比例。
令基线当前水位为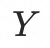
，期望的阈值水位为
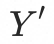，则可以得到基线需要降低流量比例为：
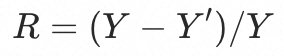
令当前n个入口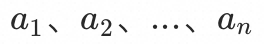
的流量比例为
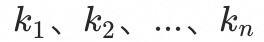，假设不降低流量的qps为
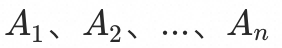，系数为
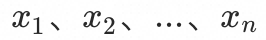，即有
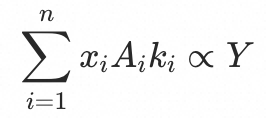
基线水位降低比例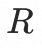
，则最终期望的基线水位为
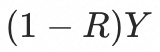，即有
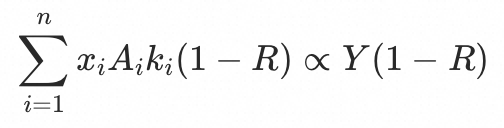
于是有入口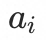
的期望流量比例
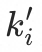为
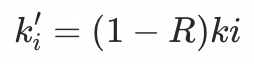
即需要降低的流量比例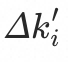
为
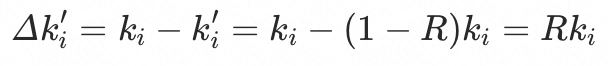
假设入口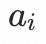
当前最多只能降低
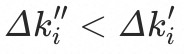的流量比例，那么我们可以认为原本应该由a_i降低的流量比例：
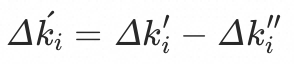
需要在下一轮的流量降低调整中，由其他入口进行调整；下一轮的流量调整中，基线还需要降低的流量比例为：
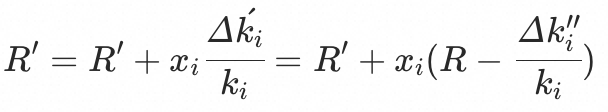
简单描述这个公式，即原本应该由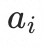
降低的流量比例在其当前流量比例的占比，再乘上当前入口在所有入口中的影响比例，得到这次原本应该由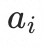降低的流量比例对基线水位比例的影响，这部分流量调整在下一轮中由其他入口承担。
▐ 流量提高算法
流量提高是站在入口视角来看的，入口的其中一个基线可以提升的倍数为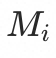
，那么这个基线允许入口增加的流量比例为
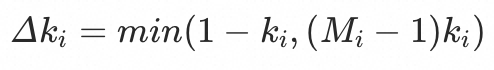
一个入口影响的基线可能有多个，最终选取能够提升得最小的一个值。
▐ 一些兜底策略
-
跌零保护
-
降低流量速率
-
慢启动
-
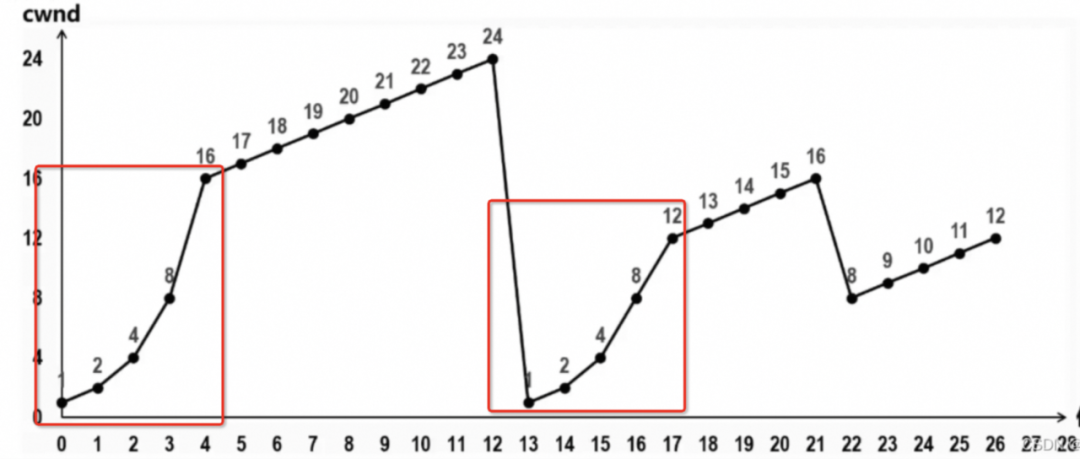
波动影响
效果
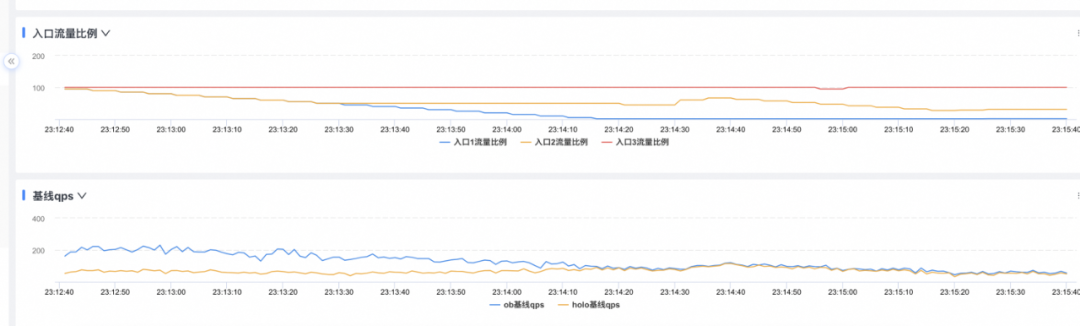
ob基线水位阈值设置为60，入口1优先级为0%，入口2优先级为50%；可见入口2比例到50%后不再降低，只降低入口1；入口1降到0依然不满足，最终入口2也降低到30%左右，保持ob基线水位在60左右。
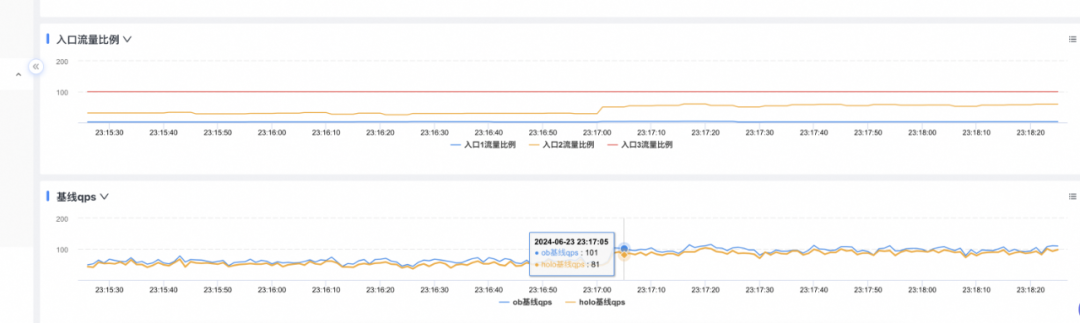
ob基线阈值回调到100，可见入口流量比例也回升，保持ob基线水位在100左右。
结语
参考资料
《奇异矩阵定义》：
https://zhuanlan.zhihu.com/p/662240649
《LU分解解线性方程组》：
https://zhuanlan.zhihu.com/p/386954541
《高斯消元解线性方程组》：
https://wuli.wiki/online/GAUSS.html
《浅说 Newton-Raphson 方法》
https://zhuanlan.zhihu.com/p/696670386
本文分享自微信公众号 - 大淘宝技术（AlibabaMTT）。
如有侵权，请联系 [email protected] 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。