
精品推荐:
《征服数据结构》专栏:50多种数据结构彻底征服
《经典图论算法》专栏:50多种经典图论算法全部掌握
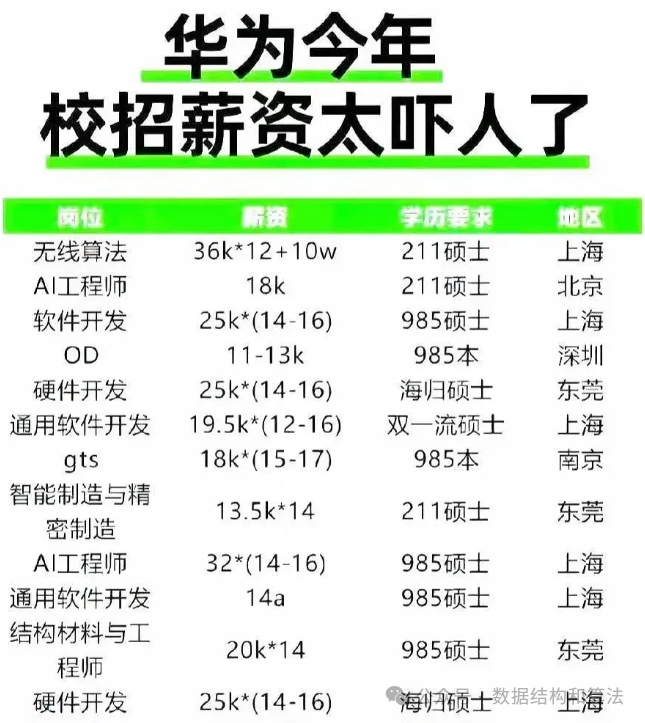
最近在网上看到一篇文章,列出了华为的校招薪资,从学历来看,要求还挺高的,不过薪资给的也高。校招最多都能给到53.2万(无线算法),所以如果学历好的话,还是建议大家学算法,下面我们就来看一道华为的算法题。
--------------下面是今天的算法题--------------
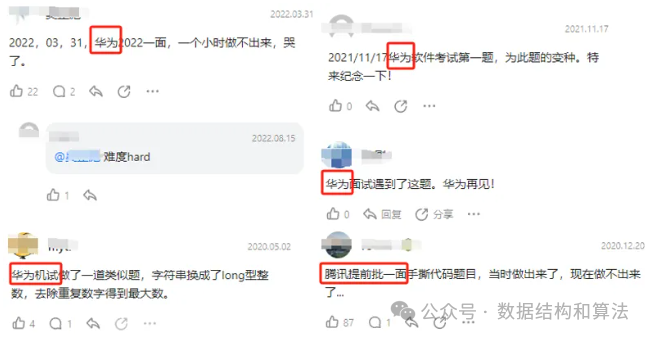
来看下今天的算法题,这题是LeetCode的第316题:去除重复字母。也是华为常考的一道算法题。
问题描述
来源:LeetCode第316题
难度:中等
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
示例1:
输入:s = "bcabc"
输出:"abc"
示例2:
输入:s = "cbacdcbc"
输出:"acdb"
1 <= s.length <= 104
s 由小写英文字母组成
问题分析
这题是让删除字符串 s 中的重复字符,使每个字符只出现一次,需要保证返回结果的字典序最小,并且还不能打乱字符的相对位置。
解决思路就是使用一个栈,然后遍历字符串中的每个字符,如果当前字符在栈中出现了就不用管了,因为每个字符只能出现一次。
如果当前字符在栈中没有出现,我们就需要把它添加到栈中,添加的时候因为要保证字典序最小,所以要和栈顶元素比较,如果当前字符比栈顶元素小并且栈顶元素在后面还会出现,就把栈顶元素给删除,接着继续重复上面的步骤。
举个例子,比如栈中元素是[a,b,e](右边是栈顶),当我们添加字符 c 的时候,因为栈顶字符 e 比当前字符 c 大:
1,假设字符串后面还有 e ,这个时候我们就可以把 e 给移除掉,在后面的时候可以在加 e 。
2,假设字符串后面没有 e 了,就不能把字符 e 给移除,因为移除之后,后面没有了就没法在添加了。
这里的关键点是怎么判断后面还有没有待移除的字符呢?很简单,我们只需要在开始的时候计算每个字符的个数即可,用掉一个就减去一个。最后栈中的字符就是需要返回的结果,我们还需要把他转化为字符串。
JAVA:
public String removeDuplicateLetters(String s) {
Stack<Character> stk = new Stack<>();// 栈
int[] count = new int[128];// 统计每个字符的数量
for (int i = 0; i < s.length(); i++)
count[s.charAt(i)]++;
// 记录对应的字符有没有添加到栈中
boolean[] add = new boolean[128];
for (char ch : s.toCharArray()) {
count[ch]--;// 遍历到当前字符,数量要减1
if (add[ch])// 如果当前字符已经添加到栈中就跳过
continue;
// 如果当前字符没有添加到栈中,栈顶字符比当前字符大
// 并且栈顶字符在后面还有,就让栈顶字符出栈。
while (!stk.isEmpty() && stk.peek() > ch
&& count[stk.peek()] > 0) {
add[stk.pop()] = false;// 标记为false
}
stk.push(ch);// 把当前字符添加到栈中
add[ch] = true;
}
// 这里是把栈中的字符转化为字符串。
StringBuilder sb = new StringBuilder();
while (!stk.isEmpty())
sb.append(stk.pop());
return sb.reverse().toString();
}C++:
public:
string removeDuplicateLetters(string s) {
stack<char> stk;// 栈
vector<int> count(128);// 统计每个字符的数量
for (char ch: s)
count[ch]++;
// 记录对应的字符有没有添加到栈中
vector<bool> add(128, false);
for (char ch: s) {
count[ch]--;// 遍历到当前字符,数量要减1
if (add[ch])// 如果当前字符已经添加到栈中就跳过
continue;
// 如果当前字符没有添加到栈中,栈顶字符比当前字符大
// 并且栈顶字符在后面还有,就让栈顶字符出栈。
while (!stk.empty() && stk.top() > ch && count[stk.top()] > 0) {
add[stk.top()] = false;
stk.pop();
}
stk.push(ch);// 把当前字符添加到栈中
add[ch] = true;
}
// 这里是把栈中的字符转化为字符串。
string str;
while (!stk.empty()) {
str.push_back(stk.top());
stk.pop();
}
reverse(str.begin(), str.end());
return str;
}Python:
def removeDuplicateLetters(self, s: str) -> str:
stk = [] # 栈
count = Counter(s) # 统计每个字符的数量
# 记录对应的字符有没有添加到栈中
add = [0] * 128
for ch in s:
count[ch] -= 1 # 遍历到当前字符,数量要减1
if add[ord(ch)]: # 如果当前字符已经添加到栈中就跳过
continue
'''
如果当前字符没有添加到栈中,栈顶字符比当前字符大
并且栈顶字符在后面还有,就让栈顶字符出栈。
'''
while stk and stk[-1] > ch and count[stk[-1]] > 0:
add[ord(stk[-1])] = 0 # 标记为false
stk.pop()
stk.append(ch) # 把当前字符添加到栈中
add[ord(ch)] = 1
# 这里是把栈中的字符转化为字符串。
return ''.join(stk)
笔者简介
博哥,真名:王一博,毕业十多年,《算法秘籍》作者,专注于数据结构和算法的讲解,在全球30多个算法网站中累计做题2000多道,在公众号中写算法题解800多题,对算法题有自己独特的解题思路和解题技巧,喜欢的可以给个关注,也可以下载我整理的1000多页的PDF算法文档。
数组,稀疏表(Sparse Table),单向链表,双向链表,块状链表,跳表,队列和循环队列,双端队列,单调队列,栈,单调栈,双端栈,散列表,堆,字典树(Trie树),ArrayMap,SparseArray,二叉树,二叉搜索树(BST),笛卡尔树,AVL树,树堆(Treap),FHQ-Treap,哈夫曼树,滚动数组,差分数组,LRU缓存,LFU缓存
……
图的介绍,图的表示方式,邻接矩阵转换,广度优先搜索(BFS),深度优先搜索(DFS),A*搜索算法,迭代深化深度优先搜索(IDDFS),IDA*算法,双向广度优先搜索,迪杰斯特拉算法(Dijkstra),贝尔曼-福特算法(Bellman-Ford),SPFA算法,弗洛伊德算法(Floyd),卡恩(Kahn)算法,基于DFS的拓扑排序,约翰逊算法(Johnson)
……