前文

我们在之前已经在GPT的帮助下用Python完成了数据处理，前文链接如下：

如何在GPT的帮助下利用Python实现数据可视化？（以INT104的Report1为例）-CSDN博客

本文将继续以INT104的Report2为例，在GPT的帮助下对数据进行分类从而分析学生的专业和各个特征之间的关系。

监督学习

1.什么是监督学习？

监督学习和后面的无监督学习最大的不同是前者是用带有标签的数据去训练模型，而后者是用没有标签的数据。

用通俗一点的话来说，现在有一个学校有重点班学生和普通班学生，重点班学生6门考试都是高分，普通班学生可能只有部分几门功课是高分，因此我们训练的时候给模型一些数据，6门都是高分的告诉模型这是重点班，不到6门高分的告诉模型这是普通班。然后模型在一定数据的训练后，发现这样的规律之后，我们再给它一个新的数据，这个人6门高分，那模型会告诉你这个是重点班学生。如果我们给它的新数据这个人有1门挂科了，那模型会告诉你这个是普通班学生。这就是监督学习的应用之一——分类器。

当然上述说的是理想情况，真实情况可能是有的是重点班的学生，但是成绩并非6门高分，会被模型判断成普通班。同理，普通班的学生也可以取得6门高分的成绩从而被模型判断成重点班的学生。这些在我们的数据处理时我们将其可以称之为异常值，这个示例也告诉我们其实现实中的数据很多时候不是理想的，比如后面我们示例中的数据也是如此。

我们需要知道的是监督学习是将数据的标签带进训练之中，我们告诉模型这个数据是哪个班的学生就是一个带标签的训练的过程。我们的问题是我们想分辨一个学生是重点班的还是普通版的，那我们带学生的班级作为标签去训练，可以快速让模型发现背后数据的规律，如果我们去掉标签训练，它会努力去发现它们之间的规律，但这个规律可能不是我们所想的。因此我们如果不太清楚数据的规律的时候可以使用无监督学习，比如我们入学考试使用无监督学习可能就可以分出两类，然后我们发现一类学习比较好，一类学习比较差，我们就将这个作为分班的依据，这就是无监督学习。无监督学习可以帮助我们发现数据中隐藏的结构和关系，然后我们使用监督学习可以将后续的同学进行预测或分类。分班依据我们找到了，现在调来了新同学，让他们再考个试，然后结果分下类分班情况就出来了。

本次Report就是想让我们用监督学习去寻找学生Programme和其他特征之间的关系，因此我们的训练标签就是Programme，然后我们用几个分类器去尝试寻找结论。

2.监督学习的方法

本次Report主要想使用决策树、SVM（Support Vector Machine）、朴素贝叶斯、集成分类器四种方法来进行探究。当然还有一些方法比如KNN等，这里并不会详细叙述。

3.开始实践

3.1 决策树

首先我们这个训练要去掉Index，这个在上篇文章的时候我们解释过，因为它其实只是一个标识符没有实际的意义。此外我们监督学习需要一个标签，前文说过因为我们要探究Programme和其他特征的关系，所以我们默认存在这样的一个关系，因此我们选择Programme作为标签。

你可以试着这样问GPT：“我现在有一个名为CW_Data的xlsx文件，其中他有11列，分别是Index、Gender、Programme、Grade、Total、MCQ、Q1、Q2、Q3、Q4、Q5，我现在想用Python对除了Index的其余10列使用决策树分类器，其中标签是Programme，然后我还想用交叉验证输出决策树模型的Accuracy和F1 score以及他们的标准误差。”

扫描二维码关注公众号，回复： 17425751 查看本文章

它会给出如下代码。

import pandas as pd
import numpy as np
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier

# 读取数据
data = pd.read_excel('CW_Data.xlsx')

# 准备特征和标签
X = data[['Gender', 'Grade', 'Total', 'MCQ', 'Q1', 'Q2', 'Q3', 'Q4', 'Q5']]
y = data['Programme']

# 创建决策树分类器
dt = DecisionTreeClassifier()

# 使用交叉验证计算准确性和F1分数
accuracy_scores = cross_val_score(dt, X, y, cv=5, scoring='accuracy')
f1_scores = cross_val_score(dt, X, y, cv=5, scoring='f1_weighted')

# 计算准确率和F1分数的标准误差
accuracy_std = np.std(accuracy_scores)
f1_std = np.std(f1_scores)

# 输出结果
print("准确性:", accuracy_scores.mean())
print("准确性标准误差:", accuracy_std)
print("F1分数:", f1_scores.mean())
print("F1分数标准误差:", f1_std)

但是我希望最后输出的结果好看一点，于是我又让它帮我修改一下。

这里我们其实可以发现在最后一行GPT给出的代码其实少了一个括号，这也是我说的GPT其实不能完全胜任所有工作，我们不能完全相信它。修改完代码，我们也可以根据自己的需求进行修改。

我们现在已经可以说完成了第一个决策树的工作了，但我们应该止步于此吗？当然不行，我们只是获得了一个数据，这个数据好吗，其实不是很好。当然这跟这个数据本身不是很理想有关，其实我们要是回忆上次PCA的图我们就知道其实它并不容易很好地分类分出来，黄色蓝色和红色几乎完全在一起，没法区分。

那让我们先看看决策树的定义。决策树每个角落节点表示一个特征或属性，每个分支代表一个判断条件，每个叶节点表示一个类别标签或一个数值，通过对特征的递归划分解决问题。

用一个比较通俗的例子，现在有一群人我们要分出他们的性别，最简单的方式当然就是用生理性别分，这样直接一个判断条件就解决了，我们也可以选择其他的判断条件，那样肯定需要好几层，这就是多个判断条件。因此我们选择判断条件都是为了减少不确定性，因此衡量不确定性的指标就是可以用来决定判断条件，因此我们会有两个判断准则——信息熵和基尼指数。信息熵代表了随机变量的不确定性；基尼系数是1-所有概率的平方从而表示不确定程度。两者都是越低表示信息越稳定。上面的代码我们发现其实它没有让我们进行选择哪一个判断条件这样的过程，因为python里面对应的方法内置了这样的功能，它会自动进行计算从而判断出最佳分裂点，因此我们不需要提前进行计算。

我们通过刚刚的定义梳理，其实我们发现决策树每次选择的依据都是局部最优解，所以他是一个贪心算法，因此可能会出现过拟合的现象，我们还可以进行剪枝的操作从而减少过拟合的情况。

我们还可以问问它决策树的那个函数有哪些参数分别代表什么意思。

你可以根据这里的所有参数，自己进行尝试，你也可以使用网格搜索暴力搜索出数据最佳的参数，但是这样一定就是过拟合了。

你也可以尝试将数据可视化出来体现不同参数的选择造成的影响。

  

我推荐的代码如下。

import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from sklearn.metrics import accuracy_score, f1_score, confusion_matrix
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.tree import DecisionTreeClassifier

# 读取数据
data = pd.read_excel('CW_Data.xlsx')

print("决策树")
# 分离特征和标签
X = data[['Gender', 'Grade', 'Total', 'MCQ', 'Q1', 'Q2', 'Q3', 'Q4', 'Q5']]  # 特征
y = data['Programme']  # 标签

# 假设你的特征都是数值型的，可以将其转换为NumPy数组
# 可能可以提高代码的效率
X_array = X.to_numpy()
y_array = y.to_numpy()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建决策树模型
dt = DecisionTreeClassifier(max_depth=4, min_samples_split=5, min_samples_leaf=1)

# 拟合模型
dt.fit(X_train, y_train)

# 输出特征重要性
print("特征重要性:")
print(dt.feature_importances_)

# 将特征重要性用柱状图呈现
plt.figure(figsize=(8, 6))
plt.barh(range(len(dt.feature_importances_)), dt.feature_importances_, align='center')
plt.yticks(range(len(dt.feature_importances_)), X.columns)
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.title('Feature Importance for Decision Tree Model')
for index, value in enumerate(dt.feature_importances_):
    plt.text(value, index, f'{value:.2f}')
plt.show()


# 预测
y_pred = dt.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)

# 计算F1分数
f1 = f1_score(y_test, y_pred, average='weighted')

# 计算混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)
# 使用 seaborn 库绘制混淆矩阵热力图
plt.figure(figsize=(8, 6))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Reds',
            xticklabels=['Predicted 1', 'Predicted 2', 'Predicted 3', 'Predicted 4'],
            yticklabels=['Actual 1', 'Actual 2', 'Actual 3', 'Actual 4'])
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.title('Confusion Matrix')
plt.show()

# 计算准确率和F1分数的标准误差（假设进行了5次交叉验证）
accuracy_scores = cross_val_score(dt, X, y, cv=5, scoring='accuracy')
f1_scores = cross_val_score(dt, X, y, cv=5, scoring='f1_weighted')

accuracy_std = np.std(accuracy_scores)
f1_std = np.std(f1_scores)

print(f'Accuracy: {np.mean(accuracy_scores):.2f} ± {accuracy_std:.2f}')
print(f'F1 Score: {np.mean(f1_scores):.2f} ± {f1_std:.2f}')

我在中间输出了一个特征贡献值，它能反应每个特征对最终预测结果的影响程度，并将其可视化了。

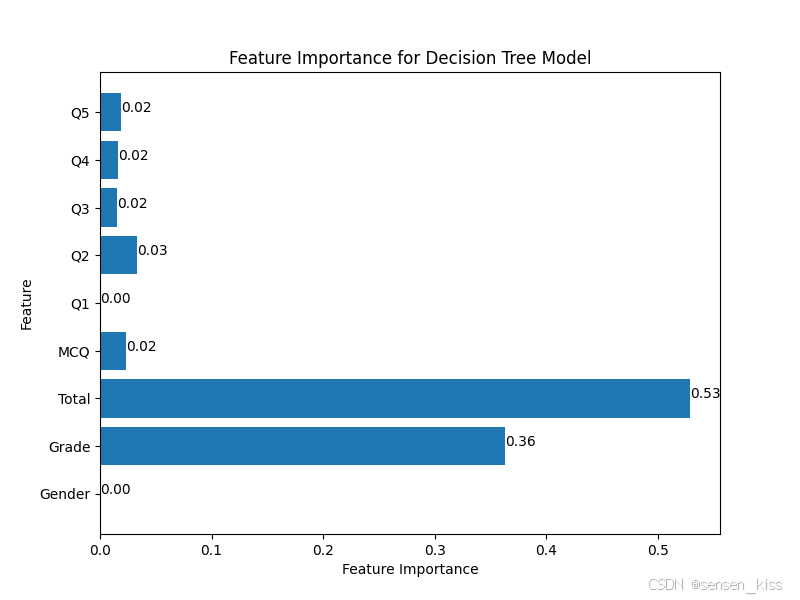
从中我们可以发现主要分辨的依据是Total和Grade。 

其中性别几乎不作为判断依据，可能是专业里的男女占比刚好都近似1比1.而Q1、Q2、Q3、Q4、Q5、MCQ组合形成了Total，因此这几个部分贡献度低而Total贡献度高。我们可以在下一个part进行验证，从而验证我们的假设是否正确。

3.2 朴素贝叶斯

实践之前我们先了解一下朴素贝叶斯的定义，我们可以通过以下的这个例子去尝试理解。

假设小明准备发一封邮件问所有同学作业答案是什么，但是收到了一些作业答案的同时，也收到了一些情书，他还有一些邮件他分辨不清是答案还是情书，所以他将之前的结果进行了一个分类，找到了答案的概率和情书的概率，并且他发现这些都有用一些共同的关键词（特征），将他们统计出来，算出对应的条件概率。

现在有一封回信，里面有关键词“喜欢”，“红豆”，于是将答案的概率乘上答案情况下喜欢的概率乘上答案情况下红豆的概率与情书的概率乘上情书的情况下喜欢的概率乘上情书的情况下红豆的概率进行比较，谁大就判断该回信是哪种。

因此朴素贝叶斯算法有以下两个问题——假设特征维度之间是独立的，但是实际情况中他们大部分互相影响，再比如这个例子中如果最后猜测情况为情书，但其实原文是喜欢红豆，那么可能就造成了错误。第二个问题是可能某个特征在一种类别中的概率是0，为了解决该问题，会使用拉普拉斯平滑技巧给每一个特征的出现次数+1，从而保证没有概率是0。

该例子来源于b站视频：[5分钟学算法] #02 朴素贝叶斯 写作业还得看小明_哔哩哔哩_bilibili

我们从刚刚的两个问题中，可以发现朴素贝叶斯其实假设特征之间是相互独立的，明显我们的这个数据不符合，因为Total是由Q1、Q2、Q3、Q4、Q5、MCQ组合而成的。

我们既可以试验这个问题，也可以验证我们刚刚的假设。我们将第一组选取的数据特征和前面决策树选择的数据特征保持一致，第二组选取的数据去掉了Gender，第三组在第一组的基础上去掉了Q1、Q2、Q3、Q4、Q5、MCQ，第四组在第三组的基础上去掉了Gender，第五组在第一组的基础上去掉了Total，而第六组在第五组的基础上去掉了Gender。我把这个最后的结果也进行了数据可视化，结果如图。

我们从上面的数据可以看出最后的数据结果相差不大，证明了我们刚刚提出的两个假设：1.性别并不影响Programme；2.由于Total是Q1、Q2、Q3、Q4、Q5、MCQ组成的，所以去掉Total或者它的组成部分并不影响最终的结果。

3.3 SVM

首先我们需要知道SVM是一个线性分类器，它的定义是最好理解的，我们尝试用一条线尽量将数据分成两类，这是它通常的应用——二元分类。其也可以用于多分类问题，使用一对一或者一对其余的方式来实现多分类。

当数据是线性可分的时候我们可以使用Hard-Margin SVM，但是其对异常值非常敏感，所以对于数据交融的情况我们一般使用Soft-Margin SVM。

在数据难以线性分割的时候我们还可以通过核函数从而将数据映射到高维空间从而在高维空间中找到更好的分割超平面。

你可以尝试直接使用SVM进行分类，最后的结果应该与前两种方法的结果差不多。

我们其实可以观察PCA的图，我们前面说过分类的依据主要是Total和Grade，我们第一次进行PCA的时候PCA的主成分也是这两个特征。

我们可以查看一下数据，发现Programme3的年级和另外三个专业的年纪不同，可能这些专业学习这门课的时间不同，因此我们可以按照这个依据做一个二元分类，将124作为一类，3单独作为一类，然后我们以Grade为依据从而进行一个二分类，代码如下。

data['Programme_bin'] = data['Programme'].apply(lambda x: 0 if x in [1, 2, 4] else 1)
X = data[['Gender', 'Grade']]
y = data['Programme_bin']
# y = data['Programme']
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建 SVM 模型并训练
svm_model = SVC(kernel='linear')
svm_model.fit(X_train, y_train)

# 预测测试集结果
y_pred = svm_model.predict(X_test)

# 计算准确率和 F1 分数
accuracy = accuracy_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred, average='weighted')

# 计算交叉验证的标准误差
f1_scores = cross_val_score(svm_model, X, y, cv=5, scoring='f1_weighted')
accuracy_scores = cross_val_score(svm_model, X, y, cv=5, scoring='accuracy')
f1_std = np.std(f1_scores)
accuracy_std = np.std(accuracy_scores)

# 打印结果
print(f'Accuracy: {np.mean(accuracy_scores):.2f} ± {accuracy_std:.2f}')
print(f'F1 Score: {np.mean(f1_scores):.2f} ± {f1_std:.2f}')

# 计算混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)
# 可视化混淆矩阵
plt.figure(figsize=(6, 6))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Reds', cbar=False,
            xticklabels=['Predicted 0', 'Predicted 1'],
            yticklabels=['Actual 0', 'Actual 1'])
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.title('Confusion Matrix')
plt.show()

最后的结果几乎是百分之一百，不是百分之百的原因也不难理解，我们从PCA的图中也可以得知，有三个学生他们可能出现了留级从而和Programme3在一个年级。

我们再次回到图上观察，我们其实可以发现红色集中在图的右侧，而黄色和蓝色集中在图的左侧，我们可以假设这是Programme1的同学大部分成绩比Programme2和Programme4高导致的。因此我们可以做一个分类器，将Programme3用Grade分出来，然后Programme1用Total分类出来。代码如下。

data['Programme_bin2'] = data['Programme'].map({2: 0, 4: 0, 1: 1, 3: 2})
X = data[['Gender', 'Grade', 'Total', 'MCQ', 'Q1', 'Q2', 'Q3', 'Q4']]
y = data['Programme_bin2']
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建 SVM 模型并训练
svm_model = SVC(kernel='linear')
svm_model.fit(X_train, y_train)

# 预测测试集结果
y_pred = svm_model.predict(X_test)

# 计算准确率和 F1 分数
accuracy = accuracy_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred, average='weighted')

# 计算交叉验证的标准误差
f1_scores = cross_val_score(svm_model, X, y, cv=5, scoring='f1_weighted')
accuracy_scores = cross_val_score(svm_model, X, y, cv=5, scoring='accuracy')
f1_std = np.std(f1_scores)
accuracy_std = np.std(accuracy_scores)

# 打印结果
print(f'Accuracy: {np.mean(accuracy_scores):.2f} ± {accuracy_std:.2f}')
print(f'F1 Score: {np.mean(f1_scores):.2f} ± {f1_std:.2f}')
# 计算混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)
# 可视化混淆矩阵
plt.figure(figsize=(6, 6))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Reds', cbar=False,
            xticklabels=['Predicted 0', 'Predicted 1', 'Predicted 2'],
            yticklabels=['Actual 0', 'Actual 1', 'Actual 2'])
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.title('Confusion Matrix')
plt.show()

最后的结果也有百分之77左右，我们可以通过观察混淆矩阵发现年级可以清晰地区分Programme3出来，但是Programme1、2、4的数据相互交融，他们无法区分，一刀切成两半肯定会有错误产生，而Programme2和Programme4几乎区分不出来，我们可以在下一章无监督学习验证我们这里的结论。 

 

3.4 集成分类器

我们可以根据前面3.3节中SVM的一些发现帮我们设计一个集成分类器。 

按照上面的思路我设计了一个投票器从而对这四类进行一个分类，第一个SVM主要将Programme3与其他Programme区分出来，而第二个SVM主要将Programme1与Programme2、4区分出来，最后再用一个SVM将Programme2和4进行一个区分。因此三层投票的权重也不同，最后的代码如下。

# 根据描述的特征选择
features_1 = ['Gender', 'Grade']
features_2 = ['Grade', 'Total', 'MCQ', 'Q1', 'Q2', 'Q3', 'Q4', 'Q5']
features_3 = ['Grade', 'Total', 'MCQ', 'Q2', 'Q3', 'Q4']

# 划分数据集
X_1 = data[features_1]
X_2 = data[features_2]
X_3 = data[features_3]
y = data['Programme']

# 将目标变量重新编码
y_1 = y.apply(lambda x: 0 if x == 3 else 1)
y_2 = y.apply(lambda x: 0 if x in [1, 3] else 1)
y_3 = y

# 划分训练集和测试集
X_train_1, X_test_1, y_train_1, y_test_1 = train_test_split(X_1, y_1, test_size=0.2, random_state=42)
X_train_2, X_test_2, y_train_2, y_test_2 = train_test_split(X_2, y_2, test_size=0.2, random_state=42)
X_train_3, X_test_3, y_train_3, y_test_3 = train_test_split(X_3, y_3, test_size=0.2, random_state=42)

# 定义分类器
clf1 = SVC(kernel='linear')
clf2 = SVC(kernel='linear')
clf3 = SVC(kernel='linear')

# 训练分类器
clf1.fit(X_train_1, y_train_1)
clf2.fit(X_train_2, y_train_2)
clf3.fit(X_train_3, y_train_3)

# 预测测试集
y_pred_1 = clf1.predict(X_test_1)
y_pred_2 = clf2.predict(X_test_2)
y_pred_3 = clf3.predict(X_test_3)
print(len(y_pred_1))
print(len(y_pred_2))
print(len(y_pred_3))

from statistics import mode

def combine_predictions(predictions):
    combined_predictions = []
    for i in range(len(predictions[0])):
        # 统计每个类别的投票结果
        list_vote = [0, 0, 0, 0]
        # 第一个分类器的投票结果

        if predictions[0][i] == 0:
            list_vote[2] += 2
        else:
            list_vote[0] += 1
            list_vote[1] += 1
            list_vote[3] += 1


        # 第二个分类器的投票结果
        if predictions[1][i] == 0:
            list_vote[0] += 1
            list_vote[2] += 1
        else:
            list_vote[1] += 1
            list_vote[3] += 1

        # 第三个分类器的投票结果
        if predictions[2][i] == 1:
            list_vote[0] += 1
        elif predictions[2][i] == 2:
            list_vote[1] += 1
        elif predictions[2][i] == 3:
            list_vote[2] += 1
        elif predictions[2][i] == 4:
            list_vote[3] += 1

        # 根据总票数计算投票结果的众数
        max_index = list_vote.index(max(list_vote))

        combined_predictions.append(max_index + 1)

    return combined_predictions

y_pred_combined = combine_predictions([y_pred_1, y_pred_2, y_pred_3])

for true_label, pred_label in zip(y_test_3, y_pred_combined):
    print(f'True Label: {true_label}, Predicted Label: {pred_label}')

# 计算混淆矩阵
conf_matrix_combined = confusion_matrix(y_test_3, y_pred_combined)
# 可视化混淆矩阵
plt.figure(figsize=(6, 6))
sns.heatmap(conf_matrix_combined, annot=True, fmt='d', cmap='Reds', cbar=False,
            xticklabels=[1, 2, 3, 4],
            yticklabels=[1, 2, 3, 4])
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.title('Confusion Matrix')
plt.show()

# 计算准确率
accuracy_combined = accuracy_score(y_test_3, y_pred_combined)

# 计算F1分数
f1_combined = f1_score(y_test_3, y_pred_combined, average='weighted')

# 打印结果
print('Combined Model Results:')
print(f'Confusion Matrix:\n{conf_matrix_combined}')
print(f'Accuracy: {accuracy_combined}')
print(f'F1 Score: {f1_combined}')

最后我将本次所有的分类器结果用可视化做成了图如下。

 

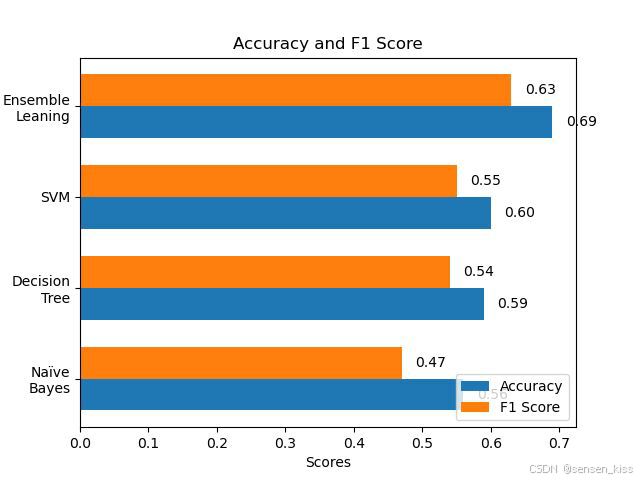
通过这张图我们也可以知道集成学习可以集各类分类器的优势从而输出出更好的结果。

你还可以尝试在集成学习里使用其他的分类器，或者在前面的一些分类器中试一试其他参数，包括ROC曲线PR曲线本文都没有详细叙述，希望大家能多多实践有所收获。

其他问题

1.概念知识

如果你对概念有一些问题，可以查看下面我当时做的概念笔记以及一些当时对我有帮助的视频。

1.1 什么是朴素贝叶斯？

 假设小明准备发一封邮件问所有同学作业答案是什么，但是收到了一些作业答案的同时，也收到了一 些情书，他还有一些邮件他分辨不清是答案还是情书，所以他将之前的结果进行了一个分类，找到了答案 的概率和情书的概率，并且他发现这些都有用一些共同的关键词（特征），将他们统计出来，算出对应的 条件概率。 现在有一封回信，里面有关键词“喜欢”，“红豆”，于是将答案的概率乘上答案情况下喜欢的概率乘上答案 情况下红豆的概率与情书的概率乘上情书的情况下喜欢的概率乘上情书的情况下红豆的概率进行比较，谁 大就判断该回信是哪种。 因此朴素贝叶斯算法有以下两个问题——假设特征维度之间是独立的，但是实际情况中他们大部分互相影 响，再比如这个例子中如果最后猜测情况为情书，但其实原文是喜欢红豆，那么可能就造成了错误。第二 个问题是可能某个特征在一种类别中的概率是0，为了解决该问题，会使用拉普拉斯平滑技巧给每一个特 征的出现次数+1，从而保证没有概率是0。

参考视频：[5分钟学算法] #02 朴素贝叶斯 写作业还得看小明_哔哩哔哩_bilibili

1.2 什么是混淆矩阵？

在最后测试的时候，将测试集的真实情况与测试结果作为横纵坐标而列出的表格，其中预测对错用True 和False表示，预测结果用Positive和Negative表示。

准确率（accuracy）是表示测试集中猜对了多少，因此是True的个数除以总个数。

精确率（precision）表示我想要的结果中正确的为多少，是Positive中True的个数，因此是True Positive 的个数除以Positive的总个数（比如我们搜索图片的时候我们会得到很多图片，但其中只有部分是正确 的） 。

召回率（recall）表示真实结果中我得到的结果的比率，是True Positive除以（True Positive + False Negative）（用1-召回率能反应我遗漏了多少）。

因此精确率和召回率在极端情况下可能会出现此消彼长的现象（全部都猜对，但是把不属于错的也猜对 了，导致precision低但是recall高。

F1值就是精确率和召回率的调和平均值，此时我们认为精确率和召回率同等重要，因此是 2*Precision*Recall除以Precision+Recall。

参考视频：【小萌五分钟】机器学习 | 混淆矩阵 Confusion Matrix_哔哩哔哩_bilibili

【小萌五分钟】机器学习 | 模型评估: 准确率 Accuracy 精确率 Precision 召回率 Recall F1值_哔哩哔哩_bilibili

1.3 什么是ROC曲线和PR曲线 ？

由于分类器是将测试结果计算概率进行判断，因此会选取阈值进行判断，不同阈值会对应不同的混淆矩 阵，将所有混淆矩阵表示在同一个二维空间即为ROC曲线。

用ROC曲线判断分类器的好坏，我们由于是一个测试集，所以分母不变，而TPR的分子是正确分类的，而 FPR的分子表示分类错误的，因此TP越大，FP越小越好，因此在图像中表现为越靠近左上角越好，或者 计算面积（AUC）进行判断。

参考视频：【小萌五分钟】机器学习 | 模型评估: ROC曲线与AUC值_哔哩哔哩_bilibili

【小萌五分钟】机器学习 | 模型评估: ROC曲线与PR曲线(一): ROC曲线与PR曲线的关系_哔哩哔哩_bilibili

【小萌五分钟】机器学习 | 模型评估: ROC曲线与PR曲线(二): ROC曲线与PR曲线的适用场景_哔哩哔哩_bilibili

1.4 什么是SVM？

SVM主要思想是寻找一个最佳的超平面将不同的类别分开，并使边界最大化。

Hard-Margin SVM：所有的都被分开。 Soft-Margin SVM：允许一些没被分开。

两个问题：1、对于一些类别相互交融时，需要引入容错率从而保证大局上的正确率。（Soft-Margin SVM） 2、对于一些线性不可分时，运用Kernel从而映射到高纬度空间去寻找超平面。

参考视频：【五分钟机器学习】向量支持机SVM: 学霸中的战斗机_哔哩哔哩_bilibili

1.5 什么是决策树？

决策树每个角落节点表示一个特征或属性，每个分支代表一个判断条件，每个叶节点表示一个类别标 签或一个数值，通过对特征的递归划分解决问题。

注：信息熵和基尼指数都是衡量数据纯度的指标，它们都是在构建过程中进行计算从而判断出最佳分裂点，因此不是提前计算从而选择，在python里方法会自动进行计算。 如果我们有多个特征想确定哪些特征对分类没有用，可以使用特征重要性进行判断，它们反映了每个特征 对分类的贡献程度，越接近1，越有用；越接近0，越没用。

决策树每次判断都希望减少不确定性，因此可以用度量不确定性的指标来决定判断条件——信息熵，基尼指数。

基尼系数：1-所有概率的平方。表示不确定程度。 因此基尼系数越小越好。

由上可知，决策树其实也是贪心算法，因此决策树的生成可能造成过拟合的现象，因此需要进行剪枝操作。 

1.6 什么是集成学习？

通过构建多个模型，并将它们组合起来从而获得更好的预测结果。（三个臭皮匠顶个诸葛亮）

集成学习可以提高模型的鲁棒性和泛化能力，减少过拟合的风险。 鲁棒性：对于异常值或扰动的抵抗能力。 泛化能力：模型在新数据前保持良好表现的能力。

1.7 什么是随机森林？

集成学习里最好的例子，通过随机选择一部分特征和样本训练决策树，并将这些决策树集合起来，从而进行预测（取均值或众数）。

优点：1、随机性强保证了不容易过拟合，抗噪性强，对异常点不敏感 2、处理高维数据相对更快 3、树状结构使模型可解释度高，可以提供每个特征的重要性。

缺点：1、过于general导致不具备正确处理过于困难样本的能力，因为随机森林的组成部分不是强分类器，且每次训练样本可能忽略了难以处理的点（Boosting可以解决这样的问题）。

参考视频：【五分钟机器学习】随机森林（RandomForest）：看我以弱搏强_哔哩哔哩_bilibili