目录
1.1. 均方误差 (Mean Squared Error, MSE)
1.2. 均方根误差 (Root Mean Squared Error, RMSE)
1.3. 平均绝对误差 (Mean Absolute Error, MAE)
2.3. 召回率 (Recall) 或灵敏度 (Sensitivity)
2.5. ROC 曲线及 AUC (Area Under Curve)
评估模型性能指标是确保预测结果准确性和可靠性的重要手段。不同的模型和算法在相同的数据集上可能会产生截然不同的预测结果，因此需要通过一系列的性能指标来量化这些差异，从而选择最优的模型进行实际应用。
根据任务类型分为回归和分类两类，分别使用不同的指标。下面我详细介绍两类任务常用的性能指标及其公式。
一、回归模型性能评估指标
1.1. 均方误差 (Mean Squared Error, MSE)
定义: MSE 衡量预测值和实际值之间的平均平方差，能够惩罚较大的误差。
公式:
MSE 值越小，模型性能越好，表示预测值与实际值之间的差距越小。
1.2. 均方根误差 (Root Mean Squared Error, RMSE)
定义: RMSE 是 MSE 的平方根，保持与原单位相同，更易解释。
公式:
RMSE 值越小，模型性能越好，表示预测值与实际值之间的差距越小。
1.3. 平均绝对误差 (Mean Absolute Error, MAE)
定义: MAE 衡量预测值和实际值之间的绝对差的平均值，不像 MSE 那样对大误差敏感。
公式:
MAE 越小，模型性能越好，表示预测值与实际值之间的差距越小。
1.4. R² (R-Squared, 决定系数)
定义: R² 衡量模型对数据的解释能力，反映了预测值与实际值的拟合程度，取值范围为 [0,1] 或更低。
公式: 
其中，yˉ是实际值的平均值。
R² 值接近 1 表示模型能很好地解释数据的变异性，越接近 0 则表明模型表现较差。
二、分类模型性能评估指标
在介绍之前会涉及到几个概念：
-
真阳性 (TP): 模型正确预测为正类的样本数量。即实际为正类且被预测为正类的样本。
-
真阴性 (TN): 模型正确预测为负类的样本数量。即实际为负类且被预测为负类的样本。
-
假阳性 (FP): 模型错误预测为正类的样本数量。即实际为负类，但被预测为正类的样本，通常称为“伪阳性”。
-
假阴性 (FN): 模型错误预测为负类的样本数量。即实际为正类，但被预测为负类的样本，通常称为“伪阴性”。
这几个概念都是用于分类模型评估的重要概念，通常在混淆矩阵中使用。
2.1. 准确率 (Accuracy)
定义: 准确率是正确预测的样本数占总样本数的比例。
公式: 
高准确率通常表示模型表现良好，但在类别不平衡时可能会产生误导，因此需结合其他指标分析。
2.2. 精确率 (Precision)
定义: 精确率是预测为正类的样本中实际为正类的比例，适用于关注假阳性的情况。
公式: 
精确率越高，模型在正类预测上越准确。
2.3. 召回率 (Recall) 或灵敏度 (Sensitivity)
定义: 召回率是实际为正类的样本中被正确预测为正类的比例，适用于关注假阴性的情况。
公式: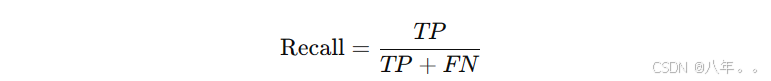
召回率越高，模型越擅长检测正类样本。
注意：精确率和召回率之间存在权衡关系，适当选择一个作为优先指标，特别是在某一类重要性更高的情况下（例如，医疗检测中的阳性病例）。
2.4. F1 分数
定义: F1 分数是精确率和召回率的调和平均值，适用于不均衡数据集。
公式: 
F1 分数综合考虑了精确率和召回率，取值范围为 [0, 1]。
2.5. ROC 曲线及 AUC (Area Under Curve)
定义: ROC 曲线描绘了假阳性率 (FPR) 与真阳性率 (TPR) 之间的关系，AUC 是 ROC 曲线下的面积，用于衡量分类模型的整体性能，取值范围为 [0, 1]。
公式:
AUC 越接近 1，表示模型区分正负类的能力越强，模型性能越好。通常，AUC ≥ 0.7 表示模型表现良好，0.8 以上则为优秀。
绘制 ROC 曲线，可以直观展示假阳性率与真阳性率的关系。
2.6. 混淆矩阵 (Confusion Matrix)
定义: 混淆矩阵是评估分类模型性能的基本工具，展示了模型预测和实际值的对应关系，形式如下：
| 实际正类 | 实际负类 | |
|---|---|---|
| 预测正类 | TP | FP |
| 预测负类 | FN | TN |
三、具体代码实现
在 Python 中，可以使用 scikit-learn 库来实现回归和分类模型的性能评估指标。以下是回归和分类性能评估的代码示例。
1、回归指标实现
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np
# 假设这是实际值和预测值
y_true = np.array([3.0, -0.5, 2.0, 7.0])
y_pred = np.array([2.5, 0.0, 2.0, 8.0])
# 计算 MSE
mse = mean_squared_error(y_true, y_pred)
print(f'Mean Squared Error (MSE): {mse}')
# 计算 RMSE
rmse = np.sqrt(mse)
print(f'Root Mean Squared Error (RMSE): {rmse}')
# 计算 MAE
mae = mean_absolute_error(y_true, y_pred)
print(f'Mean Absolute Error (MAE): {mae}')
# 计算 R²
r2 = r2_score(y_true, y_pred)
print(f'R² Score: {r2}')
2、分类指标实现
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, confusion_matrix
# 假设这是实际类标和预测类标
y_true = np.array([0, 1, 1, 0, 1, 0, 1, 0])
y_pred = np.array([0, 1, 1, 0, 0, 0, 1, 1])
# 计算准确率
accuracy = accuracy_score(y_true, y_pred)
print(f'Accuracy: {accuracy}')
# 计算精确率
precision = precision_score(y_true, y_pred)
print(f'Precision: {precision}')
# 计算召回率
recall = recall_score(y_true, y_pred)
print(f'Recall: {recall}')
# 计算 F1 分数
f1 = f1_score(y_true, y_pred)
print(f'F1 Score: {f1}')
# 计算 ROC-AUC 值 (这里需要二进制分类)
roc_auc = roc_auc_score(y_true, y_pred)
print(f'ROC-AUC Score: {roc_auc}')
# 混淆矩阵
conf_matrix = confusion_matrix(y_true, y_pred)
print(f'Confusion Matrix:\n{conf_matrix}')