深入理解二叉树、二叉查找树与平衡二叉树

在计算机科学中，树是一种重要的数据结构，用于表达层级关系或进行快速数据操作的算法优化。二叉树及其扩展结构如二叉查找树（BST）和平衡二叉树（AVL 树）是最基础、最广泛应用的树结构之一。

1. 什么是二叉树？

二叉树是一种树形结构，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。它是树结构的一个重要分支，广泛用于表达层级关系的数据结构。

二叉树的特点

节点（Node）：二叉树的基本组成元素，包含数据和指向其子节点的引用。
根节点（Root）：二叉树的顶端节点，是唯一没有父节点的节点。
叶子节点（Leaf）：没有子节点的节点，通常表示树的最底层。
内部节点（Internal Node）：有一个或两个子节点的节点。
度（Degree）：每个节点的子节点个数称为节点的度，二叉树中的节点度小于等于 2。
深度（Depth）：从根节点到某节点的路径长度称为该节点的深度，根节点深度为 0。
高度（Height）：从某节点到叶子节点的最长路径的边数称为该节点的高度，叶子节点高度为 0。

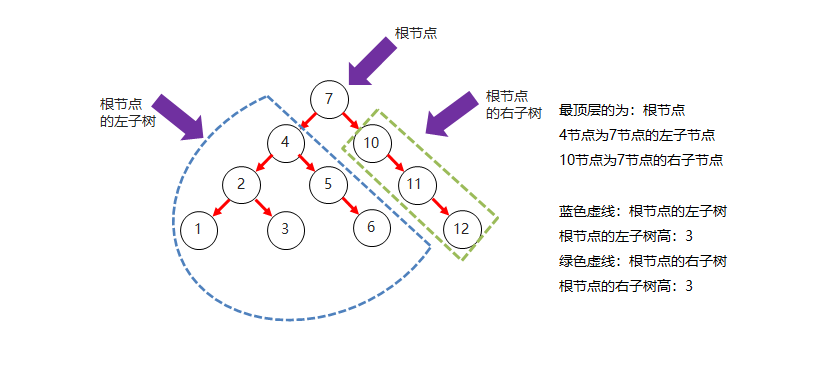
二叉树结构图

下图展示了一个典型的二叉树结构，符合二叉树的特点：

二叉树的分类

满二叉树（Full Binary Tree）：每个节点的度要么为 0，要么为 2，并且所有叶子节点都在同一层。
完全二叉树（Complete Binary Tree）：除了最后一层外，其它每一层都是满的，最后一层的所有节点从左至右连续排列。
斜二叉树：如果所有的节点都只有一个子节点，则称为斜二叉树，可以分为左斜树和右斜树。

二叉树的应用

表达式树：用于表示算术运算（如加减乘除）的结构化表达式，其中操作符为内部节点，操作数为叶子节点。
决策树：用于表示条件分支逻辑的图形化模型，如分类算法中常用的决策树。
二叉堆：实现优先队列的一种特殊二叉树结构。

2. 二叉查找树：有序数据的高效存储

二叉查找树（Binary Search Tree, BST）是一种特殊的二叉树，具有以下特点：

每个节点最多有两个子节点，分别为左子节点和右子节点。
左子树中的所有节点的值都小于根节点的值。
右子树中的所有节点的值都大于根节点的值。
这样的结构使得对于每个节点来说，其左子树的所有值小于它，右子树的所有值大于它。

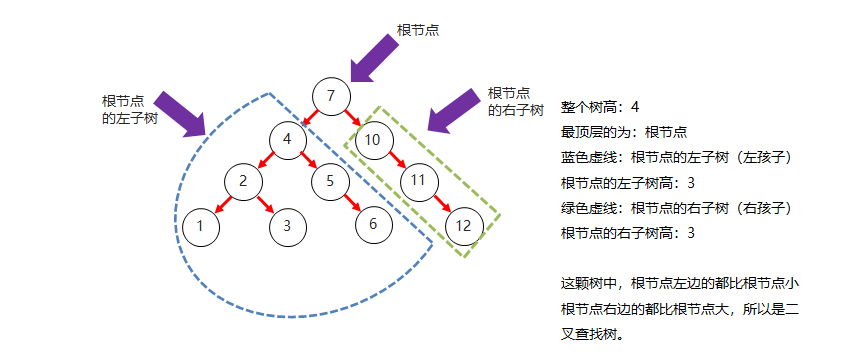
二叉查找树结构图

下图展示了一个典型的二叉查找树结构，符合二叉查找树的特点：

二叉查找树的操作

查找（Search）：
- 从根节点开始，逐个比较目标值与节点值，如果目标值小于当前节点，则进入左子树；如果大于当前节点，则进入右子树，直到找到目标节点或到达叶子节点。
- 时间复杂度为 O(h)，其中 h 是树的高度。在理想情况下（平衡状态），复杂度为 O(log n)，而在最坏情况下（退化为链表），复杂度为 O(n)。
插入（Insert）：
- 插入时从根节点开始，比较新节点的值与当前节点的值，递归选择合适的子树，直到找到空位进行插入。
- 这种递归插入方式保证了插入节点能够保持树的有序性。
删除（Delete）：
- 删除叶子节点：直接删除即可。
- 删除度为 1 的节点：用其唯一的子节点替代该节点。
- 删除度为 2 的节点：找到该节点的中序后继（右子树的最小值）或中序前驱（左子树的最大值），替代该节点的值，然后删除该替代节点。

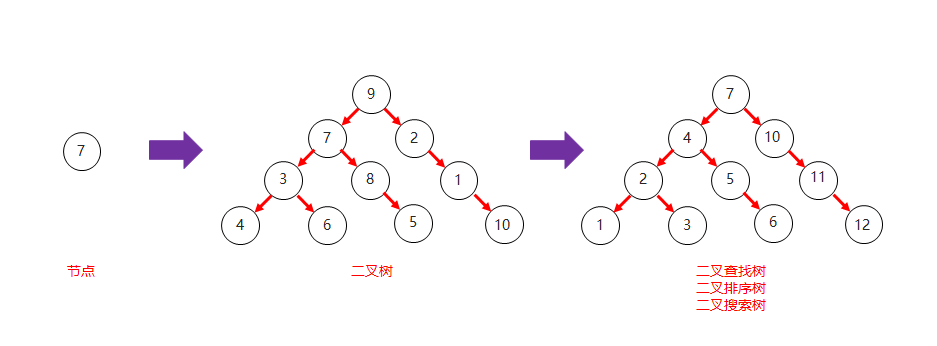
二叉查找树和二叉树对比结构图

二叉查找树的局限性

退化为链表：在极端情况下（如节点有序插入时），BST 可能退化为链表，导致时间复杂度为 O(n)，丧失了其高效性。

3. 平衡二叉树：保持高度平衡

为了防止二叉查找树退化为链表，产生不良的查找性能，引入了平衡二叉树的概念。

平衡二叉树的特点

平衡二叉树（Balanced Binary Tree，也称为 AVL 树）是保持高度平衡的二叉查找树，要求任意节点的左右子树高度差不超过 1。

扫描二维码关注公众号，回复： 17471822 查看本文章
自平衡机制：每次插入或删除节点后，如果树失去平衡性，通过旋转操作恢复平衡。
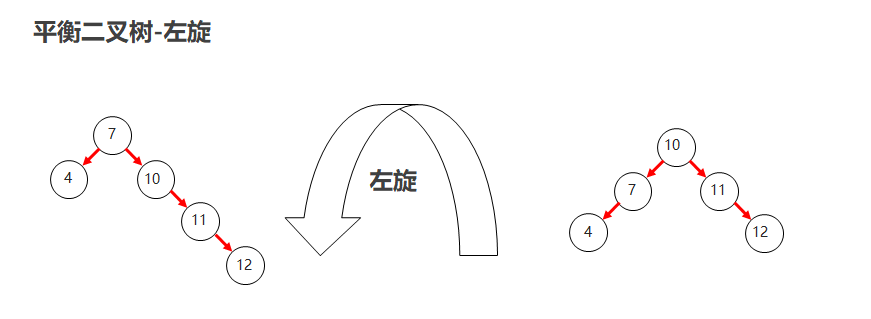
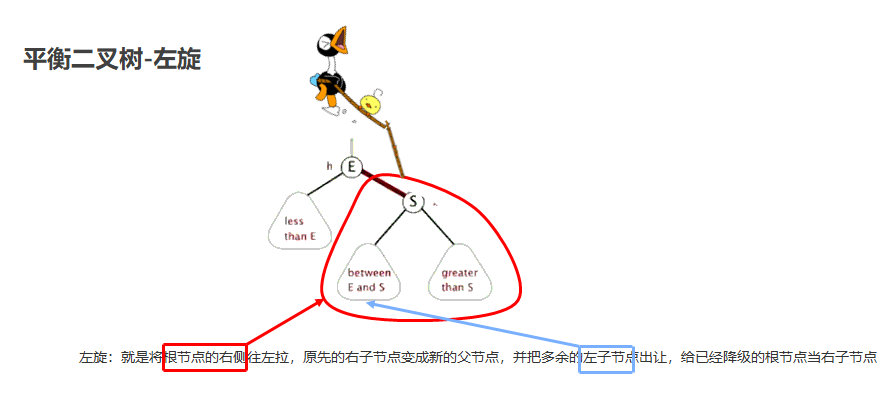
- 左旋
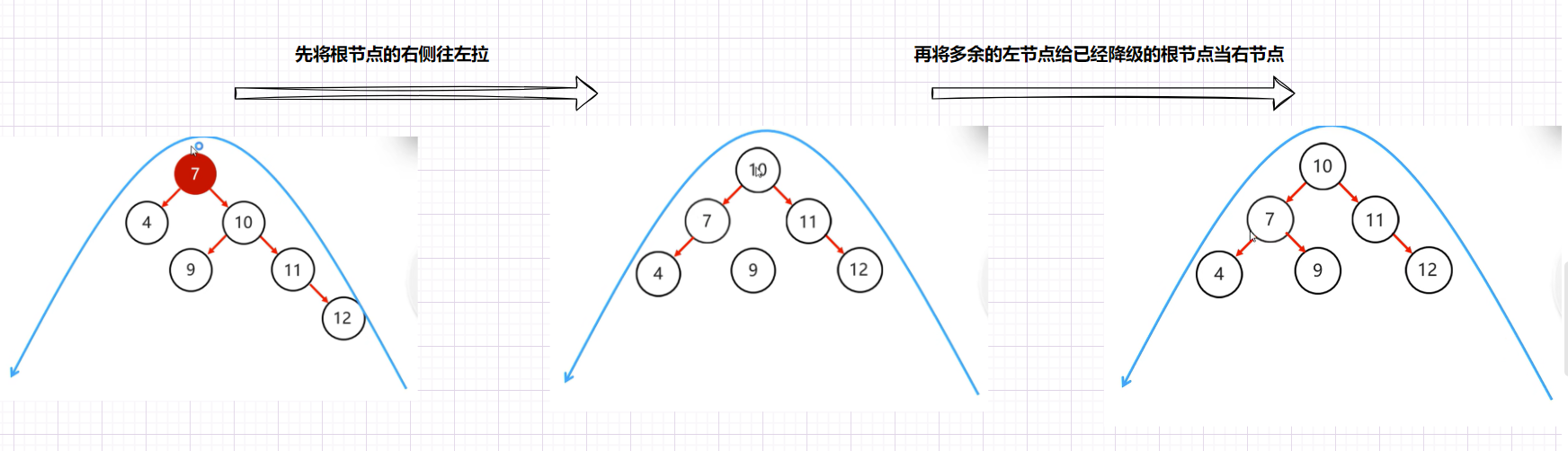
  - 就是将根节点的右侧往左拉,原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点
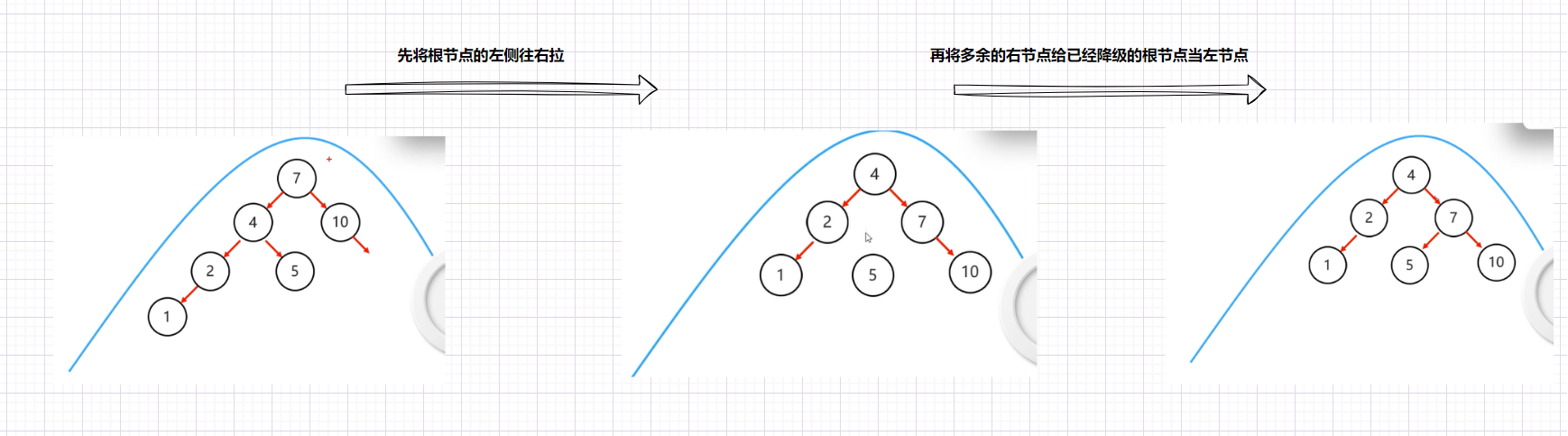
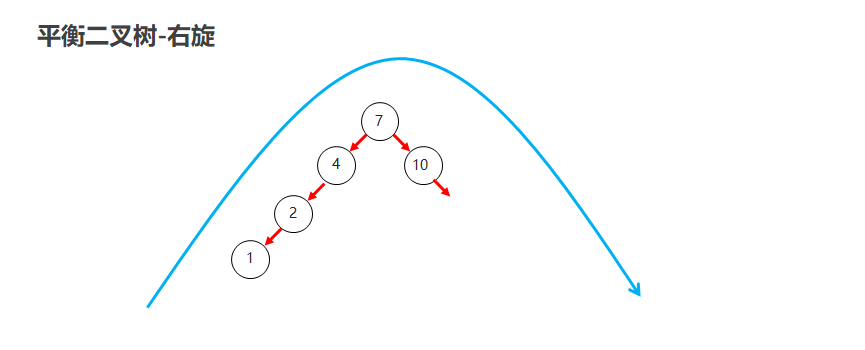
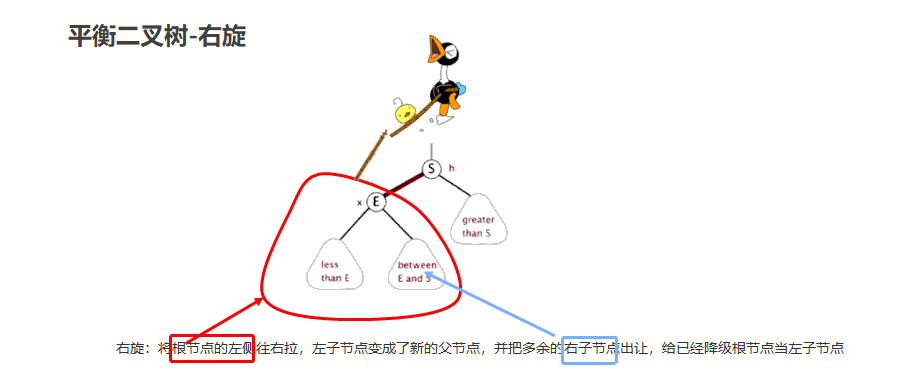
- 右旋
  - 就是将根节点的左侧往右拉,左子节点变成了新的父节点,并把多余的右子节点出让,给已经降级根节点当左子节点

平衡二叉树和二叉查找树对比结构图

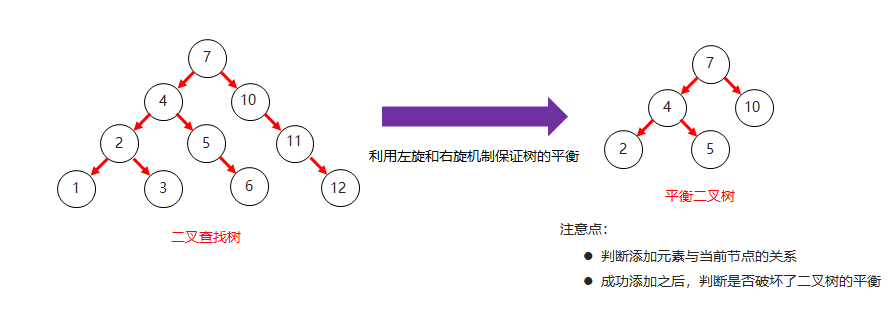
旋转操作

为了保持平衡，平衡二叉树引入了旋转操作，有以下四种类型：

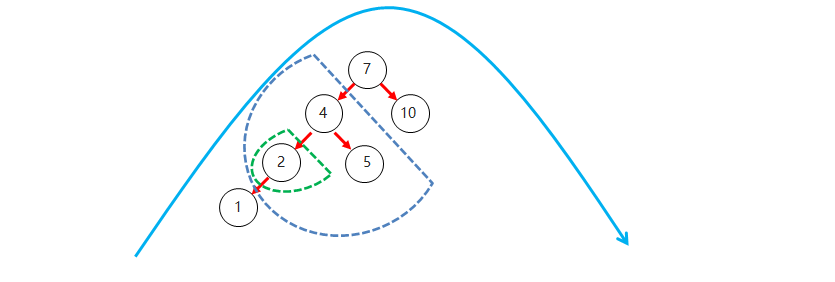
左左（LL）：如果节点的左子树的左子节点插入了新节点，导致左子树比右子树高 2，则进行右旋。
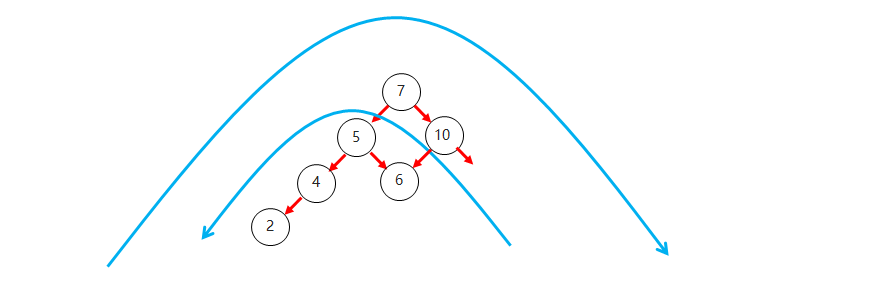
左右（LR）：如果节点的左子树的右子节点插入了新节点，导致树失去平衡，则对左子树进行左旋，然后对整体进行右旋。
右右（RR）：如果节点的右子树的右子节点插入了新节点，导致右子树比左子树高 2，则进行左旋。
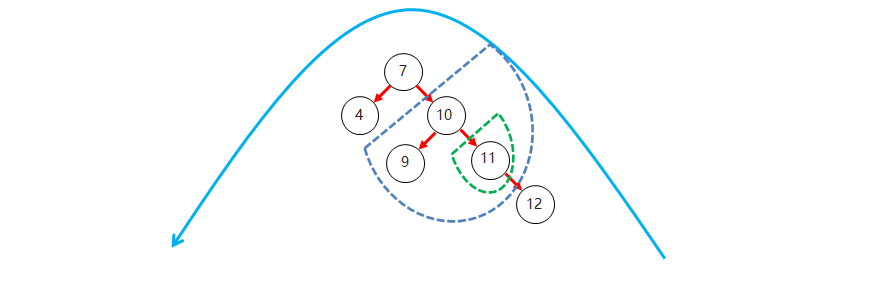
右左（RL）：如果节点的右子树的左子节点插入了新节点，导致树失去平衡，则对右子树进行右旋，然后对整体进行左旋。

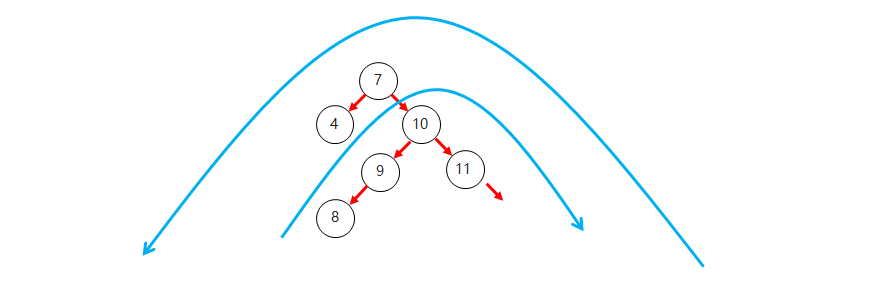
平衡二叉树的优点

在最坏情况下，AVL 树的高度为 O(log n)，保证了所有操作的时间复杂度均为 O(log n)，避免了性能退化的问题。

4. 结构对比与应用场景

二叉树 vs. 二叉查找树 vs. 平衡二叉树

二叉树：每个节点最多有两个子节点，用于一般性层级数据表示。
二叉查找树：节点按一定顺序排列，适合用于查找和存储有序数据，能提供相对高效的查找。
平衡二叉树：在二叉查找树基础上增加了平衡机制，保持左右子树高度差小，适合频繁插入、删除、查找的场景。

应用场景

二叉查找树：
- 数据库索引：二叉查找树能在有序数据中进行高效查询，适合于快速查找某个范围内的数据。
- 词典与集合：用于实现动态插入、删除和查找的操作，适用于词典、集合等数据结构的实现。
平衡二叉树：
- 自平衡数据库：例如 B 树、B+ 树，适合在磁盘上的大规模数据存储与查找。
- 操作系统调度：在一些调度算法中需要快速插入、删除调度任务时，使用 AVL 树能够保证调度的效率。

5. 树的遍历方法

二叉树的遍历是理解二叉树的重要部分，用于访问树中每一个节点。常见的遍历方法有以下几种：

前序遍历（Preorder遍历）：

遍历顺序为：根节点 -> 左子树 -> 右子树。
适合用于复制树的结构或输出表达式的前缀表达式。

实现方式：

void preorderTraversal(TreeNode* root) {
        
        
    if (root == nullptr) return;
    cout << root->val << " "; // 访问根节点
    preorderTraversal(root->left); // 遍历左子树
    preorderTraversal(root->right); // 遍历右子树
}

中序遍历（Inorder Traversal）：

遍历顺序为：左子树 -> 根节点 -> 右子树。
如果对二叉查找树进行中序遍历，得到的将是有序的数据序列。

实现方式：

void inorderTraversal(TreeNode* root) {
        
        
    if (root == nullptr) return;
    inorderTraversal(root->left); // 遍历左子树
    cout << root->val << " "; // 访问根节点
    inorderTraversal(root->right); // 遍历右子树
}

后序遍历（Postorder Traversal）：

遍历顺序为：左子树 -> 右子树 -> 根节点。
适合用于删除树中的节点或释放树的内存，因为会先处理子节点，再处理父节点。

实现方式：

void postorderTraversal(TreeNode* root) {
        
        
    if (root == nullptr) return;
    postorderTraversal(root->left); // 遍历左子树
    postorderTraversal(root->right); // 遍历右子树
    cout << root->val << " "; // 访问根节点
}

层次遍历（Level Order Traversal）：

按照从上到下、从左到右的顺序访问每一层的节点。
通常使用队列来实现，用于广度优先搜索（BFS）的方法。

实现方式：

void levelOrderTraversal(TreeNode* root) {
        
        
    if (root == nullptr) return;
    queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        
        
        TreeNode* current = q.front();
        q.pop();
        cout << current->val << " "; // 访问当前节点
        if (current->left != nullptr) q.push(current->left); // 入队左子节点
        if (current->right != nullptr) q.push(current->right); // 入队右子节点
    }
}

6. 二叉树的实际应用

表达式树：
- 表达式树是一种特定的二叉树，用于表示代数表达式，通常内部节点是运算符，叶子节点是操作数。
- 中序遍历可以输出中缀表达式，前序遍历可以输出前缀表达式，而后序遍历可以输出后缀表达式。
赫夫曼树（Huffman Tree）：
- 赫夫曼树是一种用于数据压缩的二叉树，通过构建具有最小带权路径的二叉树来实现高效编码。
- 这种树的特点是频率越高的字符距离根节点越近，从而在编码时减少数据传输量。
决策树（Decision Tree）：
- 决策树用于机器学习中的分类和回归问题。每个节点表示一个特征的判断条件，叶子节点表示决策结果。
- 决策树的构造类似于二叉树构造，通过不断将数据划分成子集，形成树形结构。
二叉堆（Binary Heap）：
- 二叉堆是一种特殊的完全二叉树，用于实现优先队列。它分为最大堆（根节点是最大值）和最小堆（根节点是最小值）。
- 常见的操作包括插入和删除，它们都可以在 O(log n) 的时间复杂度内完成。

7. 平衡二叉树与其他平衡结构对比

虽然平衡二叉树（如 AVL 树）在保持树的高度平衡性方面表现良好，但它并不是唯一的选择。还有其他自平衡树，如红黑树和B 树，它们各自有不同的应用场景和优缺点。

红黑树（Red-Black Tree）

特点：红黑树是一种近似平衡的二叉查找树，每个节点带有颜色属性（红色或黑色），通过调整节点的颜色和旋转操作保持树的平衡。
优势：
- 插入与删除操作效率高：红黑树比 AVL 树的插入和删除操作更简单，因为它不需要频繁的旋转。
- 广泛用于集合类和映射类的实现（如 C++ 中的 std::map 和 std::set）。
缺点：虽然保持了近似平衡，但不如 AVL 树严格平衡，因此查找效率比 AVL 树略低。

B 树与 B+ 树

B 树是一种用于数据库系统和文件系统中的平衡树结构。它是一种多路平衡查找树，能够在磁盘中存储大量数据，并且可以高效地进行搜索、插入和删除。
B+ 树是 B 树的扩展，每个叶子节点通过链表相连，适合范围查询，因此广泛用于数据库索引。
特点：
- 多路性：B 树的节点可以有多个子节点，避免了二叉树过深的情况，减少磁盘 I/O 操作次数。
- 性能优越：B 树和 B+ 树具有高效的随机访问能力，适用于存储和快速访问大量数据。

8. 二叉树实现的注意事项

1. 递归 vs. 非递归

在实现二叉树的遍历和操作时，递归是一种非常直观的方式，但当树的深度较大时，可能导致栈溢出。
为避免这种情况，使用显式栈来实现非递归版本的前序、中序和后序遍历是一种常见做法。

2. 空间复杂度

递归的空间复杂度与树的高度有关，即 O(h)。
对于平衡二叉树，空间复杂度是 O(log n)，而对于不平衡的二叉树（如链表结构），则可能达到 O(n)。

3. 平衡维护

在实现平衡二叉树（如 AVL 树）时，需要频繁调整节点之间的关系，以保持树的平衡。了解旋转操作的触发条件和执行方式是非常重要的。

9. 二叉树的优缺点

优点

结构简单：二叉树的节点最多有两个子节点，逻辑简单，容易理解。
查找效率：二叉查找树在平衡状态下能够保证 O(log n) 的查找效率。
灵活性：可以被扩展为其他多种结构，如 AVL 树、红黑树、B 树等，适应不同场景。

缺点

退化问题：对于二叉查找树，如果插入数据的顺序不当，可能退化为链表，导致查找效率降低。
维护成本：平衡二叉树需要通过旋转来维护平衡性，插入和删除的实现相对复杂。

10. 总结

二叉树、二叉查找树和平衡二叉树是树结构的核心组成部分。它们的各自特点和应用场景如下：

二叉树：用于基础层级数据的表示，支持多种灵活的遍历方法（前序、中序、后序、层次遍历）。
二叉查找树（BST）：通过节点值的有序排列，实现高效的查找和更新，适合用于动态数据的高效存储。
平衡二叉树（AVL 树）：通过旋转操作保持树的平衡，适合在需要频繁插入、删除的场景中保持稳定的时间复杂度。
维护成本：平衡二叉树需要通过旋转来维护平衡性，插入和删除的实现相对复杂。

10. 总结

二叉树、二叉查找树和平衡二叉树是树结构的核心组成部分。它们的各自特点和应用场景如下：

二叉树：用于基础层级数据的表示，支持多种灵活的遍历方法（前序、中序、后序、层次遍历）。
二叉查找树（BST）：通过节点值的有序排列，实现高效的查找和更新，适合用于动态数据的高效存储。
平衡二叉树（AVL 树）：通过旋转操作保持树的平衡，适合在需要频繁插入、删除的场景中保持稳定的时间复杂度。

深入理解二叉树、二叉查找树与平衡二叉树

1. 什么是二叉树？

二叉树的特点

二叉树结构图

二叉树的分类

二叉树的应用

2. 二叉查找树：有序数据的高效存储

二叉查找树结构图

二叉查找树的操作

二叉查找树和二叉树对比结构图

二叉查找树的局限性

3. 平衡二叉树：保持高度平衡

平衡二叉树的特点

平衡二叉树和二叉查找树对比结构图

旋转操作

平衡二叉树的优点

4. 结构对比与应用场景

二叉树 vs. 二叉查找树 vs. 平衡二叉树

应用场景

5. 树的遍历方法

6. 二叉树的实际应用

7. 平衡二叉树与其他平衡结构对比

红黑树（Red-Black Tree）

B 树与 B+ 树

8. 二叉树实现的注意事项

1. 递归 vs. 非递归

2. 空间复杂度

3. 平衡维护

9. 二叉树的优缺点

优点

缺点

10. 总结

10. 总结

猜你喜欢

目录

热门文章