力扣题目

解题思路

java代码

力扣题目：

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

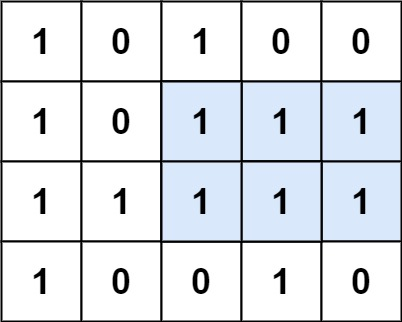
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [["0"]]
输出：0

示例 3：

输入：matrix = [["1"]]
输出：1

提示：

• rows == matrix.length
• cols == matrix[0].length
• 1 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

解题思路：

算法原理：
这道题通过计算每一行中以每个位置为起点的连续 1 的个数（即 left 数组），然后对于每一列，基于这些信息使用单调栈的方法计算最大矩形面积。

思路：

1. 首先计算 left 数组，其中 left[i][j] 表示第 i 行第 j 列的元素向左连续 1 的个数。
2. 对于每一列，通过两个单调栈分别计算每个位置向上和向下能扩展的最大行数（即 up 和 down 数组）。
3. 基于 left 、 up 和 down 数组计算每个位置对应的矩形面积，更新最大矩形面积。

代码分析：

• 外层的两个嵌套循环计算 left 数组。
• 内层的两个嵌套循环分别计算 up 和 down 数组。
• 最后的循环计算每个位置的矩形面积并更新最大值。

时间复杂度：O（mn），其中 m 是矩阵的行数， n 是矩阵的列数。主要的操作都在与矩阵大小线性相关的循环中。

空间复杂度：O（mn），用于存储 left 、 up 和 down 数组。

java代码：

package com.example.lib;

import java.util.Deque;
import java.util.LinkedList;

public class Leetocde85 {
    public static void main(String[] args) {
        System.out.println(maximalRectangle(new char[][]{
                {'1','0','1','0','0'},
                {'1','0','1','1','1'},
                {'1','1','1','1','1'},
                {'1','0','0','1','0'}
        }));
    }
    public static int maximalRectangle(char[][] matrix) {
        int m = matrix.length;
        if (m == 0) {
            return 0;
        }
        int n = matrix[0].length;
        int[][] left = new int[m][n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
                }
            }
        }

        int ret = 0;
        for (int j = 0; j < n; j++) { // 对于每一列，使用基于柱状图的方法
            int[] up = new int[m];
            int[] down = new int[m];

            Deque<Integer> stack = new LinkedList<Integer>();
            for (int i = 0; i < m; i++) {
                while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                up[i] = stack.isEmpty() ? -1 : stack.peek();
                stack.push(i);
            }
            stack.clear();
            for (int i = m - 1; i >= 0; i--) {
                while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                down[i] = stack.isEmpty() ? m : stack.peek();
                stack.push(i);
            }

            for (int i = 0; i < m; i++) {
                int height = down[i] - up[i] - 1;
                int area = height * left[i][j];
                ret = Math.max(ret, area);
            }
        }
        return ret;
    }
}

更多详细内容同步到公众号，感谢大家的支持！

每天都会给刷算法的小伙伴推送明日一题，并且没有任何收费项