

前引: 为哈程序员总爱纠结排序?排序算法不仅仅是代码工具,更是对世界运行规律的解构。下文将带你认识七种排序算法,如何将一长串数据变得“有序”,带你揭秘Google工程师偷偷藏在代码库藏的七种排序实现,以及那个改变硅谷格局的【排序算法冷战】背后的真相,作者将以零基础从各个细节详说,给每位读者带来深刻的体验,以下各种排序算法以弄清楚思想为重点,正文开始~
目录
直接插入排序
说到这个排序,我们先来看一个很有趣的日常活动:打扑克牌

我们打扑克牌,从摸到第二张牌开始,后面会逐个按照一个顺序进行比较插入 ,碰到相同大小的牌就放在一起,这样方便在出牌时打出各种组合!现在看起来,还是挺佩服这种智慧!!
算法原理:
将一个数组分为两个部分,一边是已经排序了的,另一边是未排序的,随后将新元素插入到已经排序的正确位置
实现步骤:
类比打扑克牌,第一张牌我们认为是有序的,随后从摸到的第二张牌开始,与前一张牌进行比较插入。白话文版核心思路:从第二个元素开始,分别与其前面所有的元素进行比较插入
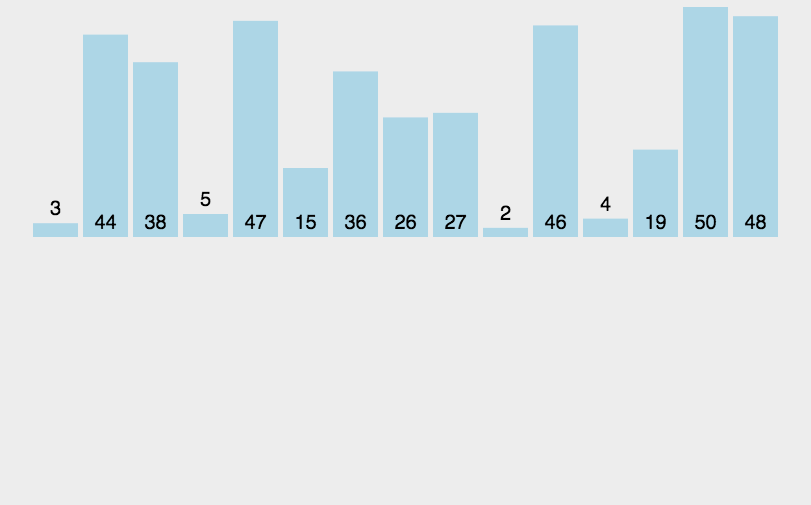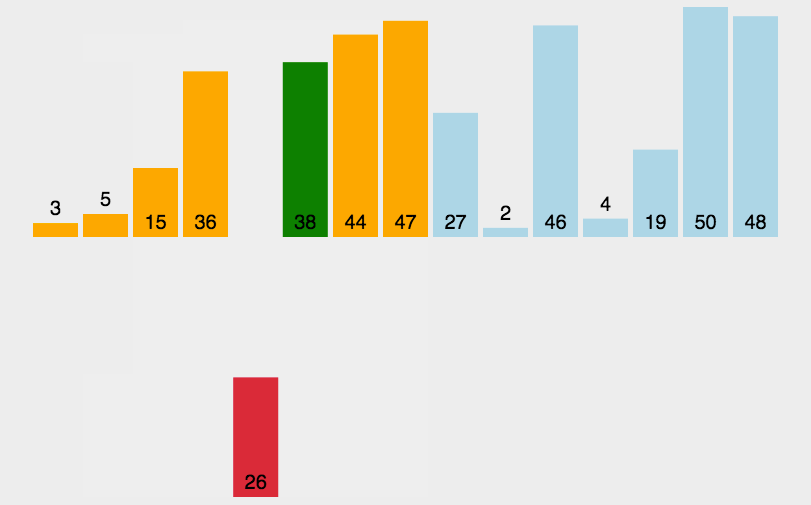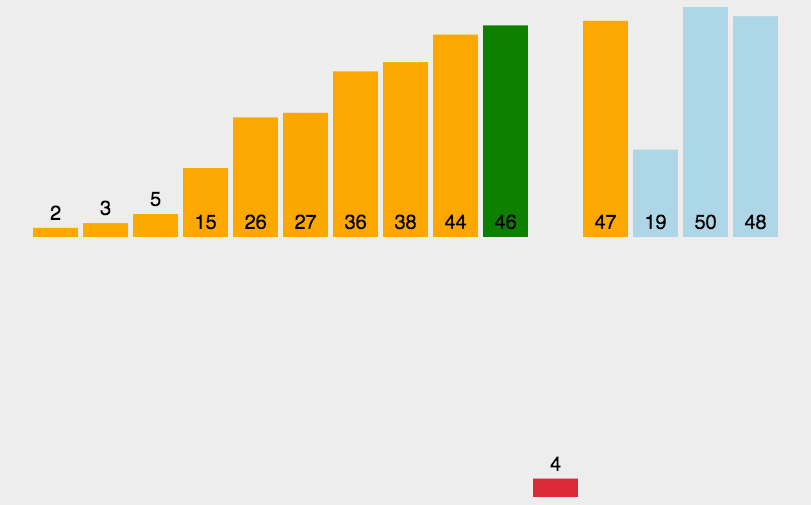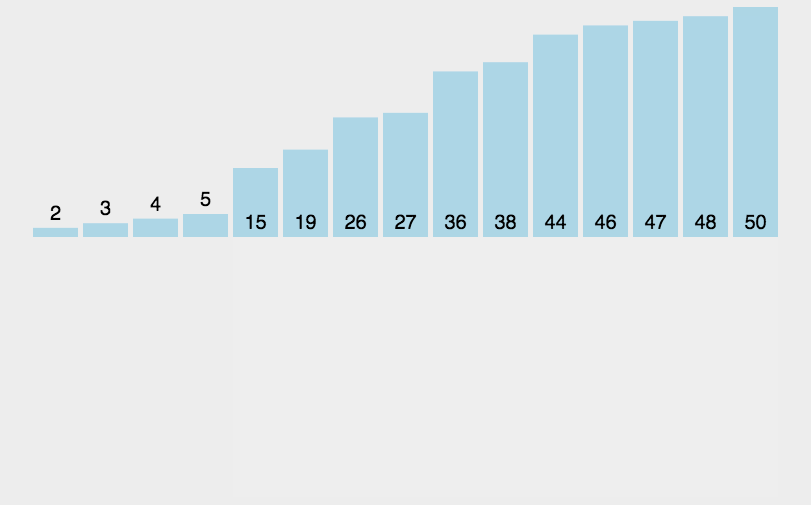
首先在这里我们第一个数组元素默认为是有序的(因为就一个元素,没有其它竞争对手)!比如

随后从第二个要插入的元素开始,依次将其与已经排序好的元素进行比较,再进行插入


最后,如果插入的元素比它当前进行比较的元素较小,就继续与其后面的元素进行比较,直到找到一个大于等于这个插入元素,然后进行插入。重复上述过程,直到全部元素变得有序
复杂度:
最好的情况就是插入的元素已经是有序的,所以最好情况是O(n)
每轮比较1次,共比较n-1次,总时间复杂度O(n-1)->O(n)
最坏情况就是插入的元素全部乱序,需要每一个都进行重新排列,最坏情况就是O(n^2)
每轮移动 i 次,总次数为(1+2+3+4+......+(n-1)=2/n(n-1))= O(n^2)
空间复杂度是在一个数组空间中进行,用中间变量交换数据,所以复杂度是O(1)
代码实现:
考虑到是零基础小白初次学习,咱们应该先写好单趟排序过程,细嚼慢咽才好理解,什么是单趟?
单趟思路:就是实现排序一个元素。当我们实现了排序一个元素,那么再加个循环,不就达到了排序整体的效果了吗?单趟循环的条件是:数组的下标不能越界,这里大家只需要按照思路实操单趟即可,并不难!
单趟实现:单趟插入的控制条件就是数组下标必须大于等于0,然后写条件判断比较元素的大小关系,如果插入的元素比其前一个有序元素小,就将这个有序元素后移换位,再与其后面一个元素比较,直到按照大小关系找到正确的位置,就结束循环开始插入,插入之后记得更新下标为有序组的最后一个元素!参考下面的代码+这段话更好理解哈!

//tmp是交换变量,end是当前正在比较元素的下标
int tmp = 0;
int end = 0;
//单趟排序
while (end >= 0)
{
if (arr[end] > tmp)
{
//元素后移
arr[end + 1] = arr[end];
end--;
}
else
break;
}
//插入
arr[end + 1] = tmp;
//重新设置下标
end = i;注意事项: 其一传数组的时候注意不要&数组名,不然就是拿的就是整个数组的地址了!
其二尽量按照代码进行动手画图,走一遍思路就通了
单趟实现之后,咱们已经实现了排序一个元素,接下来就是再套一个循环实现对整体的排序
//直接插入排序
void Insert(int* arr, int size)
{
//判空
assert(arr);
//tmp是交换变量,end是当前正在比较的元素下标
int tmp = 0;
int end = 0;
for (int i = 1; i < size; i++)
{
//赋值交换变量
tmp = arr[i];
//单趟排序
while (end >= 0)
{
if (arr[end] > tmp)
{
//元素后移
arr[end + 1] = arr[end];
end--;
}
else
break;
}
//插入
arr[end + 1] = tmp;
//重新设置下标
end = i;
}
}
分析优缺点:
此排序为稳定排序,代码量也很少,但是时间复杂度很高,效率很低,只适合小规模的数据
希尔排序
介绍:希尔排序(Shell Sort)是插入排序的一种对性能改进的直接插入版本,由Donald Shell在1959年提出。核心思想就是通过分组排序使得数据在整体上逐步达到有序,大大减少了插入排序的交换比较次数。我们知道,将一个数组分为几组,每次将一组数据进行排序,那么将这些组排序完,数据在整体上就达到了“大概”有序,所以最后还是要进行一次直接插入排序,才能真正实现完全“有序”。因此,希尔排序的整个过程可以分为以下两部分:预排序(分组排序)、直接插入排序(整体排序)
算法原理:
通过将一个数组分成多个子序列进行插入排序,逐步缩小子序列的间隔,最终完成整体有序。翻译成白话文:将一个数组分成几组,分别对每组进行直接插入排序,已达到整体有序的效果
实现步骤:
我们按照上面的算法原理,先对一个数组进行分组,这个分组并不是连续的,是有规律间断的进行分组,如下图:(注意观察每组元素的间隔)

对每个子序列(小组)分别进行直接插入排序,最后再进行一次直接插入排序,就大功告成啦!因为咱们已经有了直接插入排序的经验,所以这里的关键地方在于如何衔接变量
复杂度:
最坏情况依然是O(n^2)完全逆序、随机分布
最佳情况是O(n * log n)数据已经达到了基本有序,下面是解读:
时间复杂度取决于增量序列的选择,例如增量序列:interval=(n/2,n/4,n/8....即每次除2)
我们假设n=8,增量序列就是4,2,1
interval=4时,分为了4个子序列,每个子序列长度是2,时间为 4 * O(2^2)=O(16)
interval=2时,分为了2个子序列,每个子序列长度是4,时间为 2 * O(4^2)=O(32)
interval=1时,分为了1个子序列,每个子序列长度是8(即整体),时间为 O(8^2)=O (64)
因此我们发现:总的时间次数近似为16+32+64=112,与n^2成比例
空间复杂度O(1),仅仅需要常数级的变量进行交换数据
代码实现:
希尔排序的单趟与直接插入排序的单趟有相似之处,下面我们还是和之前一样,先实现单趟,单趟思路:顺序插入第一组无序部分的第一个元素(即下面的tmp),这里的单趟实现跟直接插入排序的单趟几乎一样,只需要注意直接插入排序是间隔为1,这里的间隔是interval

//interval是间隔
int interval=3;
//单趟
tmp = arr[end+interval];
while (end >= 0)
{
if (arr[end] > tmp)
{
//移动正在比较的元素
arr[end + interval] = arr[end];
end -= interval;
}
else
break;
}
//插入
arr[end + interval] = tmp;
end = interval;上面的单趟是排序第一组元素0跟6的,下面我们通过增加循环来实现排序完第一组,注意tmp与end的关系:tmp永远与end间隔interval个单位,咱们增加循环的实质无非就是调整end与tmp的位置,我们已经确立了tmp的关系,因此要增加的功能是通过end控制tmp,如下代码:
//interval是间隔
int interval=3;
for (int i = 0; i < size-interval; i+=interval)
{
//更新要比较元素的下标
end = i;
//单趟
tmp = arr[end + interval];
while (end >= 0)
{
if (arr[end] > tmp)
{
//移动正在比较的元素
arr[end + interval] = arr[end];
end -= interval;
}
else
break;
}
//插入
arr[end + interval] = tmp;
}我们已经实现了第一组的排序,如果我们要排序完其它组,不就是还要套一个循环吗?这个循环的功能是调整end的初始位置,在第一组end是从下标0开始,第二组、第三组的end应该分别从1、2开始,注意这两个for循环需要产生联系,如下代码及效果展示:
//interval是间隔
int interval=3;
for (int j = 0; j < interval; j++)
{
for (int i = j; i < size - interval; i += interval)
{
//更新要比较元素的下标
end = i;
//单趟
tmp = arr[end + interval];
while (end >= 0)
{
if (arr[end] > tmp)
{
//移动正在比较的元素
arr[end + interval] = arr[end];
end -= interval;
}
else
break;
}
//插入
arr[end + interval] = tmp;
}
}
上面我们已经完成了预排序的过程,再直接接入一个直接排序接口,那么整个希尔排序就完成了!
代码优化:
我们知道整个分组是通过interval来控制间隔实现的,那么这个间隔的大小对排序的影响是什么?
如果这个间隔过大:那么组之间直接跳的更快,无法高效的将数据进行一个排序,元素更大的数据无 法快速到达末尾,元素小的更无法直接到前面来
如果这个间隔过小:那么组之间跳的很慢,咱们希尔排序本来就是优化效率,间隔过小,预排序 之后越接近有序,那么最后的直接插入排序是不是有点不够效率了
优化1:
如果数据很长很长,那么它排序的分组就多一些,如果数据很短,那么它的分组就少一些,这样是不是就比我们固定间隔的方法更加高效,所以咱们的间隔应该跟数据实时长度有关
优化2:
而任何数据除2得到的数最终都是1,那么当间隔是1,就直接插入排序了,这样咱们就不用再次去接入直接插入排序的接口了,通过间隔的控制就达到了效果,从而不用再接入直接排序的接口
//interval是间隔
int interval = size;// 优化
int tmp = 0;
//end是当前正在比较的元素下标
int end = 0;
while (interval >= 1)// 优化(通过数据当前的长度动态改变间隔)
{
interval /= 2;
for (int j = 0; j < interval; j++)
{
for (int i = j; i < size - interval; i += interval)
{
//更新要比较元素的下标
end = i;
//单趟
tmp = arr[end + interval];
while (end >= 0)
{
if (arr[end] > tmp)
{
//移动正在比较的元素
arr[end + interval] = arr[end];
end -= interval;
}
else
break;
}
//插入
arr[end + interval] = tmp;
}
}
}分析优缺点:
对于未优化之前的希尔排序,常数因子小,实现简单,关键是通过循环控制变量,时间复杂度高达O(n^2),所以总体来说建议考虑其他排序算法
优化之后:显著降低了时间复杂度,适用于中等规模的排序
选择排序
算法原理:
开始整个数组都是无序的,通过不断选择剩余元素中的最小值,将其与未排序的部分的第一个元素交换位置,逐步实现整个数组的有序,每轮确定一个元素的有序
实现步骤:
开始整个数组都看成是无序的,遍历无序的部分,记录最小值,然后与未排序部分的第一个元素交换,第一个元素排序之后,记得更新再次遍历的初始位置(有序部分的末尾),一直重复就行了
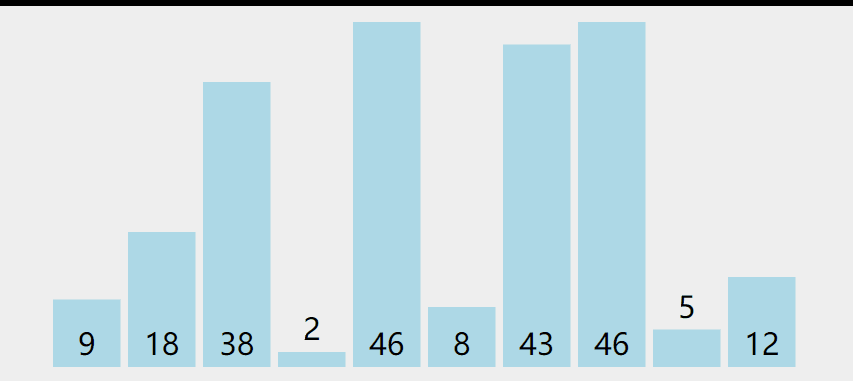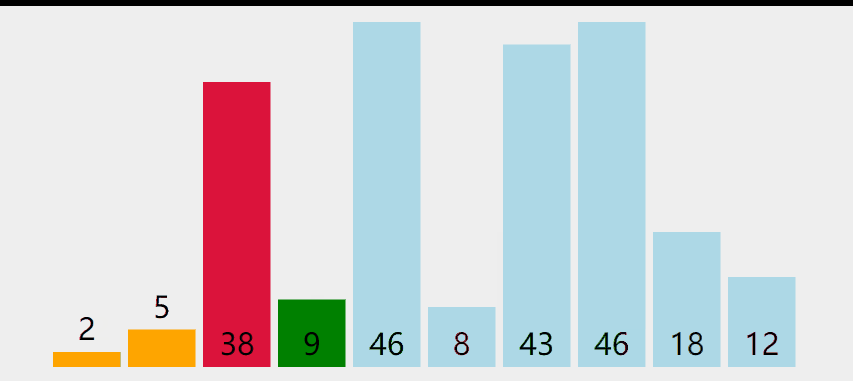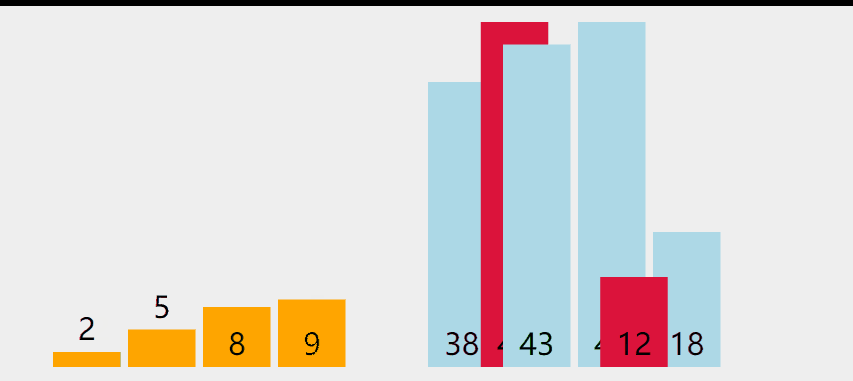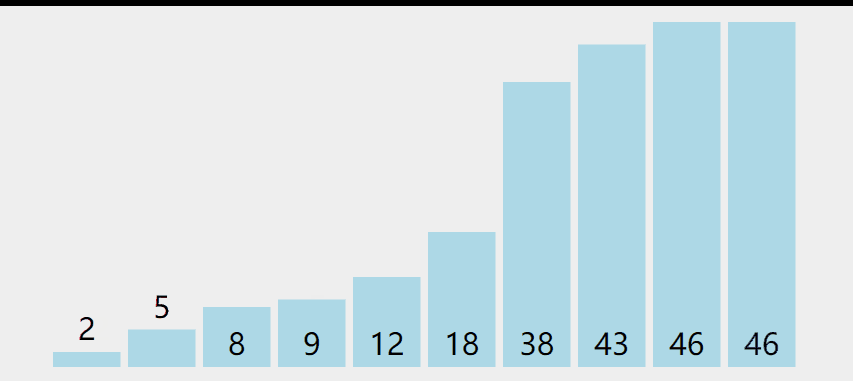
翻译成通俗白话文:从头到尾遍历找最值,每次结束在有序部分末尾开始放入遍历的最值
复杂度:
因为咱们的思路已经固定下来了,不论数组的元素是有序还是无序,都是从无序部分遍历查找,所以时间复杂度最好最坏情况都是O(n^2),下面是解读:
咱们外面的循环一共进行了(n-1)次
里面的循环一共进行了【(n)+(n-1)+(n-2)+(n-3)+.....】
总执行次数就是外面的次数 乘 里面的次数,再根据实际复杂度计算规则,得到O(n^2)
空间复杂度:咱们还是操作一个数组,所以是原地排序,复杂度为O(1),下面是解读:
咱们只创造了几个变量来表示关系,按照空间复杂度的计算规则用常数1表示所有常数,所以得到O(1)
代码实现:

我们依然先实现单趟:首先咱们知道开始整个数组都是无序的,所以我们需要从第一个元素开始遍历,找到每次遍历的最值,从数组有序组末尾开始依次进行插入,参考如下的单趟实现:

//有序部分的末尾下标
int end = 0;
//记录变量
int tmp = 0;
//用来记忆tmp的下标
int sum = 0;
//整个数组开始都是无序的,因此tmp开始等于第一个元素
tmp = arr[end];
//单趟
for (int i = end; i < size; i++)
{
//找最值(这里以找最小值为例)
if (arr[i]<tmp)
{
sum = i;
//重点:找到最小值后记得更新tmp
tmp = arr[i];
}
}
//找到最小值之后,与有序部分末尾的第一个元素交换,再更新end作为下一次开始遍历的下标
Exchange(&arr[sum], &arr[end]);
end++;
//重点:避免最小值就是它本身的情况
sum = end;我们每次从有序部分的末尾遍历,找每次遍历中无序部分的最值插入到有序部分的末尾,后面咱们按照这个思路一直到排序完为止,咱们的单趟已经排序完了第一个有序元素,因此咱们只要再套一个循环排序剩余的size-1个元素就OK了

for (int j = 0; j < size-1; j++)
{
//整个数组开始都是无序的,因此tmp开始等于第一个元素
tmp = arr[end];
//单趟
for (int i = end; i < size; i++)
{
//找最值(这里以找最小值为例)
if (arr[i]<tmp)
{
sum = i;
//重点:找到最小值后记得更新tmp
tmp = arr[i];
}
}
//找到最小值之后,与有序部分末尾的第一个元素交换,再更新end作为下一次开始遍历的下标
Exchange(&arr[sum], &arr[end]);
end++;
//重点:避免最小值就是它本身的情况
sum = end;
}分析优缺点:
选择排序是不稳定的排序算法,因为每次交换可能破坏相同元素的相对顺序,但是代码量很少,适用于小白,在学习更高效的算法之后,建议更换,它的时间效率很低,每次都需要遍历
小编寄语
排序的道路没有结束,如果数据结构排序算法篇能引发认同感!欢迎收藏点赞本文,或者分享给其它排序算法热爱者,我们的每一次互动,都可能帮助更多的人。技术的价值不在于绝对的完美,而在于精准匹配需求,预知后续佳文如何,请持续关注收藏!精彩说不定在下篇哦!
