引入

线性DP就是指状态的转移具有线性递推关系，每个状态只依赖之前的状态，按照线性顺序一步步递推下去。

正如之前在背包问题中所写到的，仍旧可以用状态表示和状态计算来解决

注意:

对于不同类的动态规划问题,核心解题步骤均为状态表示+状态计算,而如何在不同的题型中均捕捉到状态表示和状态计算的方法,才是需要通过刷题慢慢理解体会的

例题

洛谷B3637 最长上升子序列

题目描述

这是一个简单的动规板子题。

给出一个由 $n(n\le 5000)$ 个不超过 $10^6$ 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

输入

第一行，一个整数 $n$，表示序列长度。

第二行有 $n$ 个整数，表示这个序列。

输出格式

一个整数表示答案。

样例输入 #1

6
1 2 4 1 3 4

样例输出 #1

4

分析

线性DP的经典问题

状态表示： $dp[i]\to$ 前 $i$ 项且以第 $i$ 项结尾的上升子序列的最大长度

状态计算： 子状态：枚举倒数第二项 $\to dp[i]=max(dp[j]+1)(1\le j<i且a[j]<a[i])$

复杂度：$O(n^2)$

代码

// LIS
#include <iostream>

using namespace std;

const int N = 5e3 + 10;

int n;
int a[N], dp[N];

int main()
{
    
    
	cin >> n;
	
	for (int i = 1; i <= n; i ++ ) cin >> a[i];
	
	// 开始DP
	for (int i = 1; i <= n; i ++ )
	{
    
    
		dp[i] = 1;
		for (int j = 1; j < i; j ++ )
			if (a[j] < a[i])
				dp[i] = max(dp[i], dp[j] + 1);
	}
	
	int res = 0;
	for (int i = 1; i <= n; i ++ ) res = max(res, dp[i]);
	
	cout << res << endl;
    
    return 0;
}

优化

容易发现,对于每个$i$,都需要从1开始一一枚举来确定要接在哪个后面

$\Rightarrow$显然每一轮都浪费了前面得到的一些’信息’

这样浪费’信息’的行为,在动态规划中往往会有一定的优化方案,把’信息’充分利用起来

举个例子

序列: 3 1 4 2 8 6 5

对前面两项3,1,可视作2个独立的长度为1的上升子序列,

当遍历到4时，我们会发现对于4，既可以接到3上又可以接到1上，两者都是长度为1的上升子序列

容易发现，能够接到3上的一定能够接到1上 $\Rightarrow$ 长度为1的上升子序列，保留1即可，1比3适配性更强

做了这样的处理之后，我们在遍历到4时，就不用再枚举3了

所以我们需要做的就是实时维护这样一个前面 $i-1$ 项里面各个长度的最优上升子序列的末尾元素，以判断第 $i$ 项能否接上去

这步的复杂度仍旧为 $O(n)$，需要优化，能否用二分优化？

判断这样一个最优上升子序列末尾元素的值的序列的性质，形如下图：

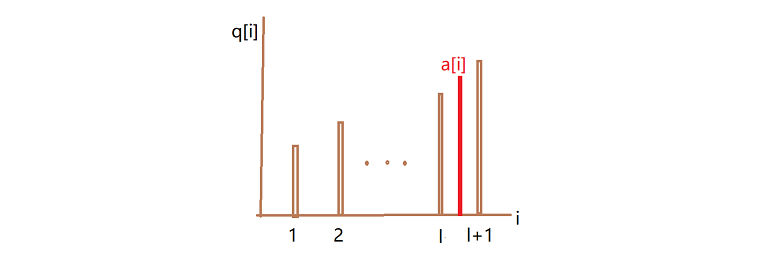
设 $q[j]$ 代表长度为 $j$ 的上升子序列的末尾项，假设我们 $a[i]$ 最优情况下接到长度为 $x$的上升子序列后面

则必有 $q[x]<a[i]\le q[x+1]$ ，否则$a[i]$接到 $q[x+1]$ 后面更长

则 $q[j]$ 必定是一个单调不减的序列 $\Rightarrow$ 具有二段性，可以二分

由此，该步复杂度降低至 $O(logn)$，整体复杂度优化到 $O(nlogn)$

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 5e3 + 10;

int n;
int a[N], q[N];
int len = 0;

int main()
{
    
    	
	cin >> n;
    
    memset(q, 0x3f, sizeof q);
    q[0] = 0;
    
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    
    for (int i = 1; i <= n; i ++ )
    {
    
    
    	// 开始二分
		int l = 0, r = len;
		int mid;
		
		while (l < r)
		{
    
    
			// 找到可以接的最大值
			mid = l + r + 1>> 1;
			if (q[mid] < a[i]) l = mid;
			else r = mid - 1;
		}
		
		// 接在长度为l的后面,维护q
		q[l + 1] = min(q[l + 1], a[i]);
		len = max(len, l + 1);
    }
    
    cout << len << endl;
    
    return 0;
}

思考

读者看到这里也许会有疑问,为何状态表示方式要这样定?其他的表示方式不行码?

正如背包问题中对第 $i$ 件物品有选与不选之分,为何我这里状态表示里第 $i$ 项必须选呢?

$\Rightarrow$ 状态表示: $dp[i]\to$ 前 $i$ 项的里面最长的上升子序列长度

这样子在动态规划完之后就不需要再定一个 $res$ 一个个取 $max$ 来求最大值了, $dp[n]$ 直接就是答案

$但方便的状态表示带来的代价是难以甚至无法进行状态计算$

在上述状态中,由于 $dp[j]$ 的 $j$ 可能选可能没有选,我们根本就找不到子状态来进行状态转移

$\Rightarrow$ 状态表示和状态转移是相互制约的,一个易就会有一个难,当找不到转移方程时,不妨尝试换一种表示方法

洛谷P1439 【模板】最长公共子序列

题目描述

给出 $1,2,\dots ,n$ 的两个排列 $P_1$ 和 $P_2$ ，求它们的最长公共子序列。

输入

第一行是一个数 $n$。

接下来两行，每行为 $n$ 个数，为自然数 $1,2,\dots ,n$​ 的一个排列。

$n\le 10^5$

输出

一个数，即最长公共子序列的长度。

样例输入 #1

5 
3 2 1 4 5
1 2 3 4 5

样例输出 #1

3

仍旧是子序列问题,经过前一道题的尝试之后,思考一下这道题要如何进行状态表示和状态计算吧~

分析

状态表示: $dp[i][j]\to P_1$的前 $i$ 项, $P_2$ 的前 $j$ 项的最长公共子序列长度

状态计算: 子节点包含于

$$dp[i][j]=\{\begin{array}{ll}dp[i][j-1]& \text{选 }{P}_1[i]\text{，不选 }{P}_2[j]\\ dp[i-1][j]& \text{不选 }{P}_1[i]\text{，选 }{P}_2[j]\\ dp[i-1][j-1]+1& \text{选 }{P}_1[i]\text{，选 }{P}_2[j]\\ dp[i-1][j-1]& \text{不选 }{P}_1[i]\text{，不选 }{P}_2[j]\end{array}$$

注意:这里只是包含,各个状态之间囊括的集合可能存在交集,但是并集一定是全集,不影响正确性

且 $dp[i-1][j-1]$一定会包含于 $dp[i-1][j]$ 和 $dp[i][j-1]$ 中,故可以舍去

复杂度: $O(n^2)$

代码

// LCS
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n;
int a[N], b[N];
int dp[N][N]; // 爆了

int main()
{
    
    	
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> n;
	
	for (int i = 1; i <= n; i ++ ) cin >> a[i];
	for (int i = 1; i <= n; i ++ ) cin >> b[i];
	
	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= n; j ++ )
		{
    
    
			dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			if (a[i] == b[j])
				dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
		} 
		
	cout << dp[n][n] << endl;
	
	return 0;
}

嗯?等等! $n\le 10^5$? hhh 说好的模板呢

显然这题用朴素的公共子序列方法时间复杂度肯定是过不去的,至少需要优化到$ O(nlogn) $

想不出.jpg 看到 $LIS$ 的优化做法,恰好也是 $O(nlogn)$ 哎,要是能拿来用就好了!

优化

假设两个序列分别为

$P_1:52431$

$P_2:23145$

容易发现最长公共子序列为 $[2,3,1]$

做这样的处理,把 $P_1$ 的元素进行变换，第 $i$ 项映射为 $i$,即

$5\to 1$

$2\to 2$

$4\to 3$

$3\to 4$

$1\to 5$

变换之后序列为

$P_1:12345$

$P_2:24531$

最长公共子序列变为了$[2,4,5]$

容易发现，变换之后的公共子序列均为 $P_2$ 的上升子序列

由此，问题便转化为了求变换后的 $P_2$ 的最长上升子序列，在上一题的优化做法中可以把复杂度优化至$O(nlogn)$

代码

// LCS → LIS
#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e5 + 10;

int n;
int a[N], b[N], c[N];
int q[N];

int main()
{
    
    	
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> n;
	
	for (int i = 1; i <= n; i ++ ) cin >> a[i];
	for (int i = 1; i <= n; i ++ ) cin >> b[i];
	
	// c[i]存储映射关系
	for (int i = 1; i <= n; i ++ ) c[a[i]] = i;
	
	// b[i]进行变换
	for (int i = 1; i <= n; i ++ ) b[i] = c[b[i]];
	
	// 开始求最长上升子序列
	memset(q, 0x3f, sizeof q);
	q[0] = 0;
	int len = 0;
	for (int i = 1; i <= n; i ++ )
	{
    
    
		int l = 0, r = len;
		int mid;
		while (l < r)
		{
    
    
			mid = l + r + 1 >> 1;
			if (q[mid] < b[i]) l = mid;
			else r = mid - 1;
		}
		
		q[l + 1] = min(q[l + 1], b[i]);
		len = max(len, l + 1);
	}
		
	cout << len << endl;
	
	return 0;
}

既然已经解决了 $LIS$ 和 $LCS$ 问题，来试试二者的结合吧~

洛谷 LCIS

再来看看其它情景下的线性DP

洛谷P1216 数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

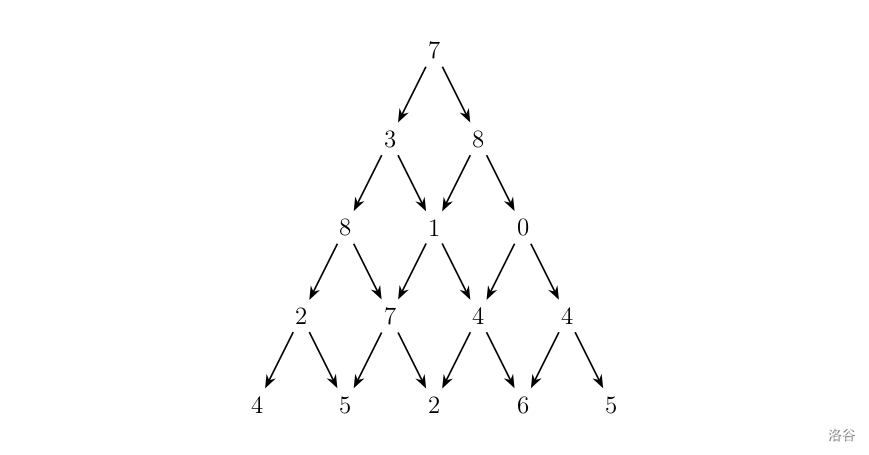
在上面的样例中，从 $7\to 3\to 8\to 7\to 5$ 的路径产生了最大权值。

输入

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

$1\le r\le 1000$，所有输入在 $[0,100]$ 范围内

输出

单独的一行,包含那个可能得到的最大的和。

样例输入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出 #1

30

:::

思路

直接把三角形拉直，想象为一个正方形被沿对角线对半分了

状态表示：$dp[i][j]\to$ 走到第 $i$ 行第 $j$ 列的最大值

状态计算：$dp[i][j] = max(dp[i-1][j], dp[i-1][j+1]) + a[i][j] $

代码

#include<iostream>

using namespace std;

const int N = 1e3 + 10,INF=1e9;

int dp[N][N];//存最大值
int a[N][N];//存三角形

int n;

int main()
{
    
    
	cin >> n;

	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= i; j++) cin >> a[i][j];

	//初始化边界
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n + 1; j++)	dp[i][j] = -INF;

	dp[1][1] = a[1][1];
	for (int i = 2; i <= n; i++)
		for (int j = 1; j <= n; j++) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];

	int maxn = 0;

	for (int i = 1; i <= n; i++) maxn = max(maxn, dp[n][i]);

	cout << maxn;

	return 0;
}

进阶一点的数字三角形

洛谷P1006 传纸条

题目描述

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排坐成一个 $m$ 行 $n$ 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 $(1,1)$，小轩坐在矩阵的右下角，坐标 $(m,n)$。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 $0$ 表示），可以用一个 $[0,100]$ 内的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入

第一行有两个用空格隔开的整数 $m$ 和 $n$，表示班里有 $m$ 行 $n$ 列。

接下来的 $m$ 行是一个 $m\times n$ 的矩阵，矩阵中第 $i$ 行 $j$ 列的整数表示坐在第 $i$ 行 $j$ 列的学生的好心程度。每行的 $n$​ 个整数之间用空格隔开。

$1\le m,n\le 50$

输出

输出文件共一行一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

样例输入 #1

3 3
0 3 9
2 8 5
5 7 0

样例输出 #1

34

结语

看了这么多道线性DP的题目，容易发现其实线性DP的状态表示还是比较好想到的，基本上都是围绕着题目的问题来设置递推的状态，难点就在一些优化上，尽量把层与层之间暴力枚举的复杂度给消去