注:本文为 “积分电路与微分电路” 相关文章合辑。
图片清晰度,限于引文原状。
如有内容异常,请看原文。
RC 电路(积分电路,微分电路)
2011-08-13 10:42:12
RC 电路是电阻器电容器电路(RC 电路)或者 RC 过滤器,RC 网络是电路与电容器组成的电路,由电阻器电压或电流源驱动。一次 RC 电路由一个电阻器和一个电容器组成,是 RC 电路的简单例子。RC 电路在模拟电路、脉冲数字电路中得到广泛应用。
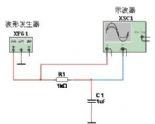
RC 电路的分类
(1)RC 串联电路

电路特点:由于有电容存在,不能流过直流电流,电阻和电容都对电流存在阻碍作用,其总阻抗由电阻和容抗确定,总阻抗随频率变化而变化。RC 串联有一个转折频率: f 0 = 1 2 π R 1 C 1 f_0 = \frac{1}{2 \pi R_1 C_1} f0=2πR1C11。
当输入信号频率大于 f 0 f_0 f0 时,整个 RC 串联电路的总阻抗基本不变,其大小等于 R 1 R_1 R1。
(2)RC 并联电路
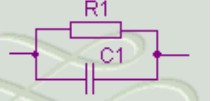
RC 并联电路既可通过直流又可通过交流信号。它和 RC 串联电路有着同样的转折频率: f 0 = 1 2 π R 1 C 1 f_0 = \frac{1}{2 \pi R_1 C_1} f0=2πR1C11。当输入信号频率小于 f 0 f_0 f0 时,信号相对电路为直流,电路的总阻抗等于 R 1 R_1 R1;当输入信号频率大于 f 0 f_0 f0 时, C 1 C_1 C1 的容抗相对很小,总阻抗为电阻阻值并上电容容抗。当频率高到一定程度后,总阻抗为 0。
(3)RC 串并联电路
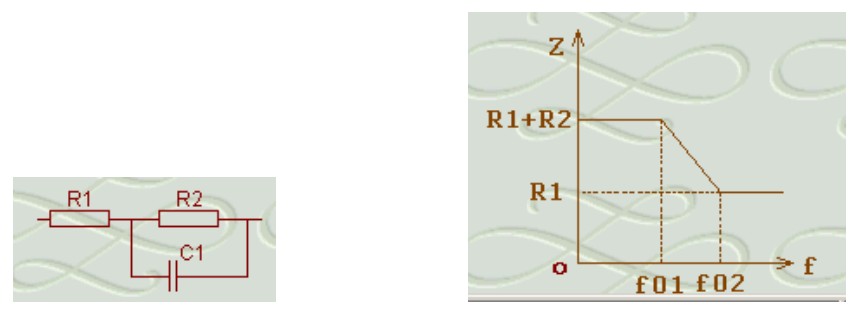
RC 串并联电路存在两个转折频率 f 01 f_{01} f01 和 f 02 f_{02} f02:
f 01 = 1 2 π R 2 C 1 , f 02 = 1 2 π C 1 [ R 1 R 2 ( R 1 + R 2 ) ] f_{01} = \frac{1}{2 \pi R_2 C_1}, \quad f_{02} = \frac{1}{2 \pi C_1 \left[ \frac{R_1 R_2}{(R_1 + R_2)} \right]} f01=2πR2C11,f02=2πC1[(R1+R2)R1R2]1
当信号频率低于 f 01 f_{01} f01 时, C 1 C_1 C1 相当于开路,该电路总阻抗为 R 1 + R 2 R_1 + R_2 R1+R2。
当信号频率高于 f 02 f_{02} f02 时, C 1 C_1 C1 相当于短路,此时电路总阻抗为 R 1 R_1 R1。
当信号频率高于 f 01 f_{01} f01 低于 f 02 f_{02} f02 时,该电路总阻抗在 R 1 + R 2 R_1 + R_2 R1+R2 到 R 1 R_1 R1 之间变化。
积分电路的作用是:消减变化量,突出不变量。RC 电路的积分条件是 R C ≥ T k RC \geq T_k RC≥Tk, T k T_k Tk 是脉冲周期。积分电路可将矩形脉冲波转换为锯齿波或三角波,还可将锯齿波转换为抛物波。电路原理基于电容的充放电原理,电路的时间常数 R × C R \times C R×C 必须大于或等于 10 倍于输入波形的宽度。
微分电路的作用是:消减不变量,突出变化量。微分电路可把矩形波转换为尖脉冲波,电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出,而对恒定部分则没有输出。输出的尖脉冲波形的宽度与 R × C R \times C R×C 有关(即电路的时间常数), R × C R \times C R×C 越小,尖脉冲波形越尖,反之则宽。此电路的 R × C R \times C R×C 必须远远小于输入波形的宽度,否则就失去了波形变换的作用,变为一般的 RC 耦合电路。一般 R × C R \times C R×C 少于或等于输入波形宽度的 1 10 \frac{1}{10} 101 就可以了。
在模拟及脉冲数字电路中,常常用到由电阻 R R R 和电容 C C C 组成的 RC 电路。在这些电路中,电阻 R R R 和电容 C C C 的取值不同、输入和输出关系以及处理的波形之间的关系,产生了 RC 电路的不同应用。下面分别介绍微分电路、积分电路、耦合电路、脉冲分压器以及滤波电路。
1. RC 微分电路
如图 1 所示,电阻 R R R 和电容 C C C 串联后接入输入信号 V I V_I VI,由电阻 R R R 输出信号 V O V_O VO。当 R C RC RC 数值与输入方波宽度 t W t_W tW 之间满足 R C ≪ t W RC \ll t_W RC≪tW 时,这种电路就称为微分电路。在 R R R 两端(输出端)得到正、负相间的尖脉冲,而且发生在方波的上升沿和下降沿,如图 2 所示。

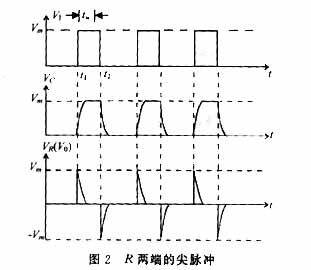
在 t = t 1 t = t_1 t=t1 时, V I V_I VI 由 0 → V m V_m Vm,因电容上电压不能突变(来不及充电,相当于短路, V C = 0 V_C = 0 VC=0),输入电压 V I V_I VI 全降在电阻 R R R 上,即 V O = V R = V I = V m V_O = V_R = V_I = V_m VO=VR=VI=Vm。随后( t > t 1 t > t_1 t>t1),电容 C C C 的电压按指数规律快速充电上升,输出电压随之按指数规律下降(因 V O = V I − V C = V m − V C V_O = V_I - V_C = V_m - V_C VO=VI−VC=Vm−VC),经过大约 3 τ 3\tau 3τ( τ = R × C \tau = R \times C τ=R×C)时, V C ≈ V m V_C \approx V_m VC≈Vm, V O ≈ 0 V_O \approx 0 VO≈0。 τ \tau τ( R C RC RC)的值愈小,此过程愈快,输出正脉冲愈窄。
在 t = t 2 t = t_2 t=t2 时, V I V_I VI 由 V m V_m Vm → 0,相当于输入端被短路,电容原先充有左正右负的电压 V m V_m Vm 开始按指数规律经电阻 R R R 放电。刚开始,电容 C C C 来不及放电,其左端(正电)接地,所以 V O = − V m V_O = - V_m VO=−Vm,之后 V O V_O VO 随电容的放电也按指数规律减小,同样经过大约 3 τ 3\tau 3τ 后,放电完毕,输出一个负脉冲。
只要脉冲宽度 t W > ( 5 ∼ 10 ) τ t_W > (5 \sim 10)\tau tW>(5∼10)τ,在 t W t_W tW 时间内,电容 C C C 已完成充电或放电(约需 3 τ 3\tau 3τ),输出端就能输出正负尖脉冲,才能成为微分电路,因而电路的充放电时间常数 τ \tau τ 必须满足: τ < ( 1 5 ∼ 1 10 ) t W \tau < \left( \frac{1}{5} \sim \frac{1}{10} \right) t_W τ<(51∼101)tW,这是微分电路的必要条件。
由于输出波形 V O V_O VO 与输入波形 V I V_I VI 之间恰好符合微分运算的结果 V O = R C ( d V I d t ) V_O = RC \left( \frac{\mathrm{d} V_I}{\mathrm{d} t} \right) VO=RC(dtdVI),即输出波形是取输入波形的变化部分。如果将 V I V_I VI 按傅里叶级展开,进行微分运算的结果,也将是 V O V_O VO 的表达式。它主要用于对复杂波形的分离和分频器,如从电视信号的复合同步脉冲分离出行同步脉冲和时钟的倍频应用。
2. RC 耦合电路
如图 3 所示,如果电路时间常数 τ \tau τ( R C RC RC) ≫ t W \gg t_W ≫tW,它将变成一个 RC 耦合电路。输出波形与输入波形一样。
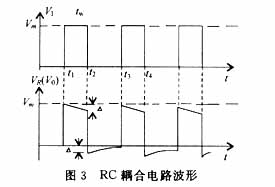
(1)在 t = t 1 t = t_1 t=t1 时,第一个方波到来, V I V_I VI 由 0 → V m V_m Vm,因电容电压不能突变( V C = 0 V_C = 0 VC=0), V O = V R = V I = V m V_O = V_R = V_I = V_m VO=VR=VI=Vm。
(2) t 1 < t < t 2 t_1 < t < t_2 t1<t<t2 时,因 τ ≫ t W \tau \gg t_W τ≫tW,电容 C C C 缓慢充电, V C V_C VC 缓慢上升为左正右负, V O = V R = V I − V C V_O = V_R = V_I - V_C VO=VR=VI−VC, V O V_O VO 缓慢下降。
(3)在 t = t 2 t = t_2 t=t2 时, V O V_O VO 由 V m V_m Vm → 0,相当于输入端被短路,此时, V C V_C VC 已充有左正右负电压 Δ [ Δ = ( V I τ ) × t W ] \Delta \left[ \Delta = \left( \frac{V_I}{\tau} \right) \times t_W \right] Δ[Δ=(τVI)×tW],经电阻 R R R 非常缓慢地放电。
(4)在 t = t 3 t = t_3 t=t3 时,因电容还来不及放完电,积累了一定电荷,第二个方波到来,电阻上的电压就不是 V m V_m Vm,而是 V R = V m − V C V_R = V_m - V_C VR=Vm−VC( V C ≠ 0 V_C \neq 0 VC=0),这样第二个输出方波比第一个输出方波略微往下平移,第三个输出方波比第二个输出方波又略微往下平移,……,最后,当输出波形的正半周“面积”与负半周“面积”相等时,就达到了稳定状态。也就是电容在一个周期内充得的电荷与放掉的电荷相等时,输出波形就稳定不再平移,电容上的平均电压等于输入信号中电压的直流分量(利用 C C C 的隔直作用),把输入信号往下平移这个直流分量,便得到输出波形,起到传送输入信号的交流成分的作用,因此是一个耦合电路。
以上的微分电路与耦合电路,在电路形式上是一样的,关键是 t W t_W tW 与 τ \tau τ 的关系。下面比较一下 τ \tau τ 与方波周期 T T T( T > t W T > t_W T>tW)不同时的结果,如图 4 所示。在这三种情形中,由于电容 C C C 的隔直作用,输出波形都是一个周期内正、负“面积”相等,即其平均值为 0,不再含有直流成分。
① 当 τ ≫ T \tau \gg T τ≫T 时,电容 C C C 的充放电非常缓慢,其输出波形近似理想方波,是理想耦合电路。
② 当 τ = T \tau = T τ=T 时,电容 C C C 有一定的充放电,其输出波形的平顶部分有一定的下降或上升,不是理想方波。
③ 当 τ ≪ T \tau \ll T τ≪T 时,电容 C C C 在极短时间内( t W t_W tW)已充放电完毕,因而输出波形为上下尖脉冲,是微分电路。

3. RC 积分电路
如图 5 所示,电阻 R R R 和电容 C C C 串联接入输入信号 V I V_I VI,由电容 C C C 输出信号 V 0 V_0 V0。当 R C RC RC( τ \tau τ)数值与输入方波宽度 t W t_W tW 之间满足 τ ≫ t W \tau \gg t_W τ≫tW 时,这种电路称为积分电路。


在 t = t 2 t = t_2 t=t2 时, V I V_I VI 由 V m V_m Vm → 0,相当于输入端被短路,电容原先充有左正右负电压 V I V_I VI( V I < V m V_I < V_m VI<Vm)经 R R R 缓慢放电, V O V_O VO( V C V_C VC)按指数规律下降。
这样,输出信号就是锯齿波,近似为三角形波, τ ≫ t W \tau \gg t_W τ≫tW 是本电路必要条件,因为它是在方波到来期间,电容只是缓慢充电, V C V_C VC 还未上升到 V m V_m Vm 时,方波就消失,电容开始放电,以免电容电压出现一个稳定电压值。而且 τ \tau τ 越大,锯齿波越接近三角波。输出波形是对输入波形积分运算的结果,突出输入信号的直流及缓变分量,降低输入信号的变化量。
4. RC 滤波电路(无源)
在模拟电路中,由 RC 组成的无源滤波电路根据电容的接法及大小主要可分为低通滤波电路(如图 7)和高通滤波电路(如图 8)。


(1)在图 7 的低通滤波电路中,它与积分电路有些相似(电容 C C C 都是并联在输出端),但它们应用在不同的电路功能上。积分电路主要是利用电容 C C C 充电时的积分作用,在输入方波情形下,来产生周期性的锯齿波(三角波),因此电容 C C C 及电阻 R R R 是根据方波的 t W t_W tW 来选取的。而低通滤波电路是将较高频率的信号旁路掉(因 X C = 1 2 π f C X_C = \frac{1}{2 \pi f C} XC=2πfC1, f f f 较大时, X C X_C XC 较小,相当于短路),因而电容 C C C 的值是参照低频点的数值来确定的。对于电源的滤波电路,理论上 C C C 值愈大愈好。
(2)图 8 的高通滤波电路与微分电路或耦合电路形式相同。在脉冲数字电路中,因 R C RC RC 与脉宽 t W t_W tW 的关系不同而区分为微分电路和耦合电路;在模拟电路中,选择恰当的电容 C C C 值,就可以有选择性地让较高频的信号通过,而阻断直流及低频信号。例如,高音喇叭串接的电容可以阻止中低音进入高音喇叭,以免烧坏。另一方面,在多级交流放大电路中,它也是一种耦合电路。
5. RC 脉冲分压器
当需要将脉冲信号经电阻分压传到下一级时,由于电路中存在各种形式的电容,如寄生电容,它相当于在负载侧接有一负载电容(如图 9)。当输入一脉冲信号时,因电容 C L C_L CL 的充电,电压不能突变,使输出波形前沿变坏,失真。为此,可在 R 1 R_1 R1 两端并接一加速电容 C 1 C_1 C1,这样组成一个 RC 脉冲分压器(如图 10)。


在 t = 0 + t = 0^+ t=0+ 时,电容视为短路,电流只流经 C 1 C_1 C1 和 C L C_L CL, V O V_O VO 由 C 1 C_1 C1 和 C L C_L CL 分压得到:
V o ( 0 + ) = V C L ( 0 + ) = V m × C 1 / ( C 1 + C L ) V_{o}(0^{+}) = V_{C_{L}}(0^{+})=V_{m}\times C_{1}/(C_{1}+C_{L}) Vo(0+)=VCL(0+)=Vm×C1/(C1+CL)
(2) t = ∞ t = \infty t=∞ 时,电容视为开路,电流只流经 R 1 R_{1} R1, R 2 R_{2} R2, V o V_{o} Vo 由 R 1 R_{1} R1 和 R 2 R_{2} R2 分压得到:
V o ( ∞ ) = V R 2 ( ∞ ) = V m × R 2 / ( R 1 + R 2 ) V_{o}(\infty)=V_{R_{2}}(\infty)=V_{m}\times R_{2}/(R_{1}+R_{2}) Vo(∞)=VR2(∞)=Vm×R2/(R1+R2)
V o ( 0 + ) = V o ( ∞ ) V_{o}(0^{+}) = V_{o}(\infty) Vo(0+)=Vo(∞) 时,输出波形就是输入波形经分压后不失真传输(如图 11 (b))。即:
V m × [ C 1 / ( C 1 + C L ) ] = V m × [ R 2 / ( R 1 + R 2 ) ] V_{m}\times [C_{1}/(C_{1}+C_{L})]=V_{m}\times [R_{2}/(R_{1}+R_{2})] Vm×[C1/(C1+CL)]=Vm×[R2/(R1+R2)]
C 1 = C L × R 2 / R 1 C_{1}=C_{L}\times R_{2}/R_{1} C1=CL×R2/R1
C 1 < C L × R 2 / R 1 C_{1}<C_{L}\times R_{2}/R_{1} C1<CL×R2/R1, V o ( 0 + ) < V o ( ∞ ) V_{o}(0^{+})<V_{o}(\infty) Vo(0+)<Vo(∞) 时,出现欠补偿;
C 1 > C L × R 2 / R 1 C_{1}>C_{L}\times R_{2}/R_{1} C1>CL×R2/R1, V o ( 0 + ) > V o ( ∞ ) V_{o}(0^{+})>V_{o}(\infty) Vo(0+)>Vo(∞) 时,出现过补偿。
但是,任何信号源都有一定的内阻,以及一些电路的需要,通常采取过补偿的办法。例如,在电视信号中,为突出传送图像的轮廓,采用勾边电路,就是通过加大 C 1 C_1 C1 的取值。
求 RC 电路的放电时间为 1 分钟,电压从 9V 降到 5V。放电电流为 300mA 左右,选择最佳的 R R R 值和 C C C 值。
RC 电路的放电方程是: U C = U S e − t / ( R C ) U_C = U_S e^{-t / (RC)} UC=USe−t/(RC)
其中, U S = 9 U_S = 9 US=9, U C = 5 U_C = 5 UC=5, t = 60 t = 60 t=60,代入公式可求出时间常数 R C RC RC 的值。
现在关键就是确定 R R R 和 C C C 的值,它只能通过所要求的放电电路来选择。
由放电电流公式: I = C d U d t , I = C \frac{\mathrm{d}U}{\mathrm{d}t}, I=CdtdU,
再将此公式代入上面的公式中可得: I = − U S C R C e − t / ( R C ) I = - \frac{U_S C}{RC} e^{-t / (RC)} I=−RCUSCe−t/(RC)
将 C C C 看成一个未知参数,然后作出 I − t I - t I−t 曲线,计算出该曲线与直线 I = 300 I = 300 I=300 所围成的面积,这个积分上下限为 t = 0 t = 0 t=0 到 60,使面积最小的 C C C 值即可。
积分器与微分器简单原理介绍
Posted on 2019-11-20 19:28 by qpoling
一、积分器

电容两端电压 u c u_c uc 和流过的电流 i c i_c ic 之间为微分和积分关系,即:
i c = C d u c d t i_{c}=C\frac{\mathrm{d}u_{c}}{\mathrm{d}t} ic=Cdtduc
u c = 1 C ∫ i c d t u_{c}=\frac{1}{C}\int i_{c}{\mathrm{d}t} uc=C1∫icdt
根据虚短和虚断,以及节点电流方程:
u I R = − C d u 0 d t ⇒ u 0 = − 1 R C ∫ u I d t \frac{u_I}{R}= -C\frac{\mathrm{d}u_{0}}{\mathrm{d}t}\ \Rightarrow\ u_{0}=-\frac{1}{RC}\int u_{I}{\mathrm{d}t} RuI=−Cdtdu0 ⇒ u0=−RC1∫uIdt
也可将电容视为“阻抗”来分析电路:
s ↔ d d t ↔ j w = j 2 π f s\leftrightarrow\frac{\mathrm{d}}{\mathrm{d}t}\leftrightarrow jw = j2\pi f s↔dtd↔jw=j2πf
1 s ↔ ∫ d t ↔ 1 j w = 1 j 2 π f \frac{1}{s}\leftrightarrow\int {\mathrm{d}t}\leftrightarrow\frac{1}{jw}=\frac{1}{j2\pi f} s1↔∫dt↔jw1=j2πf1
因此,利用反相比例放大器结果可知:
u o u i = − 1 R s C \frac{u_{o}}{u_{i}}=-\frac{1}{RsC} uiuo=−RsC1
二、微分器

根据虚地和节点电流方程可知:
C d u I d t = − u o R C\frac{\mathrm{d}u_{I}}{\mathrm{d}t}=-\frac{u_{o}}{R} CdtduI=−Ruo
由上式,输出电压与输入电流的关系为:
u o = − R C d u I d t u_{o}=-RC\frac{\mathrm{d}u_{I}}{\mathrm{d}t} uo=−RCdtduI
同样将电容视为阻抗,得:
u o = − R s C u I = − R C d u I d t u_{o} = -RsCu_{I} = -RC\frac{\mathrm{d}u_{I}}{\mathrm{d}t} uo=−RsCuI=−RCdtduI
补充:
-
在积分电路的实用电路中,为了集成运放输入平衡,在同相输入端串联平衡电阻。并且为防止低频信号增益过大,常在电容上并联一个大电阻对低频(直流)增益加以限制。
-
在微分电路中,为防止高频信号增益过大,造成电路不稳定,常在电容上串联一个小电阻。
积分电路和微分电路的工作原理
By 李逍遥,2019-07-29 17:12:05
一、积分电路和微分电路概念
微分电路 可把矩形波转换为尖脉冲波,此电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出。
积分电路 可将矩形脉冲波转换为锯齿波或三角波,还可将锯齿波转换为抛物波。电路原理基于电容的充放电原理。电路的时间常数 R × C R \times C R×C 是关键,构成积分电路的条件是电路的时间常数必须大于或等于 10 倍于输入波形的宽度。
二、积分电路概念效果图

当输入信号电压加在输入端时,电容 C C C 上的电压逐渐上升,而其充电电流则随着电压的上升而减小。电流通过电阻 R R R 和电容 C C C 的特性可以用下面的公式表达:
i = ( V R ) e − ( t / C R ) i = \left( \frac{V}{R} \right) e^{-(t / CR)} i=(RV)e−(t/CR)
- i i i:充电电流(A)
- V V V:输入信号电压(V)
- C C C:电阻值(欧姆)
- e e e:自然对数常数(2.71828)
- t t t:信号电压作用时间(秒)
- C R CR CR: R × C R \times C R×C 常数
由此可以找出输出部分即电容上的电压为 V − i × R V - i \times R V−i×R,结合上面的计算,我们得出输出电压曲线计算公式为:
V c = V [ 1 − e − ( t / C R ) ] V_c = V \left[ 1 - e^{-(t / CR)} \right] Vc=V[1−e−(t/CR)]
三、微分电路概念效果图

当第一个方波电压加在微分电路的两端(输入端)时,电容 C C C 上的电压开始因充电而增加,而流过电容 C C C 的电流则随着充电电压的上升而下降。电流经过微分电路( R R R、 C C C)的规律可以用下面的公式来表达:
i = ( V R ) e − ( t / C R ) i = \left( \frac{V}{R} \right) e^{-(t / CR)} i=(RV)e−(t/CR)
- i i i:充电电流(A)
- V V V:输入信号电压(V)
- C C C:电阻值(欧姆)
- e e e:自然对数常数(2.71828)
- t t t:信号电压作用时间(秒)
- C R CR CR: R × C R \times C R×C 常数
由此可以找出输出部分即电阻上的电压为 i × R i \times R i×R,结合上面的计算,我们得出输出电压曲线计算公式为:
V c = V [ e − ( t / C R ) ] V_c = V \left[ e^{-(t / CR)} \right] Vc=V[e−(t/CR)]
运算放大器积分电路及积分电路设计
By VirtuousLiu,2020-04-04 15:15:52
积分电路 Integrator Circuit
在运算放大器积分器电路中,电容器插入反馈环路中,并在反相输入端与 R 1 R_1 R1 一起产生一个 R C RC RC 时间常数。
积分的物理意义
积分的物理意义在许多领域都有应用,例如:
- 加速度对时间的积分是速度。
- 速度对时间的积分是路程。
- 功率对时间的积分是功。
积分的几何意义
几何意义来源于数学基础概念,例如几何处理等问题。

积分电路
积分器电路根据电路时间常数和放大器的带宽,在一个频率范围内输出输入信号的积分。输入信号被施加到反相输入,因此输出相对于输入信号的极性反相。理想的积分器电路会饱和到电源轨,具体取决于输入失调电压的极性,并需要增加一个反馈电阻 R 2 R_2 R2,以提供稳定的直流工作点。反馈电阻器限制了执行积分功能的较低频率范围。
设计须知
- 对于反馈电阻,应使用尽可能大的值。
- 选择一个 CMOS 运算放大器,以最小化输入偏置电流的误差。
- 放大器的增益带宽积(GBP)将设置积分器功能的上限频率。集成功能的有效性通常在距放大器带宽约十年的时间开始降低。
- 需要将一个可调基准电压连接到运算放大器的同相输入,以消除输入失调电压,否则较大的 DC 噪声增益将导致电路饱和。具有非常低的失调电压的运算放大器可能不需要这样做。
积分电路如下所示:


积分电路计算
积分电路输出电压 V o u t V_{out} Vout 计算:

如何设计
- 需要先设定电阻值,即上图中的 R 1 R_1 R1。
- 计算 C 1 C_1 C1 以设置单位增益积分频率。
- 计算 R 2 R_2 R2 将下限截止频率设置为比最小工作频率低十倍。
- 选择增益带宽至少为所需最大工作频率的 10 倍的放大器。

增益带宽积
假设运算放大器的增益带宽积为 1 MHz,这意味着当频率为 1 MHz 时,器件的增益下降到单位增益。即此时 A = 1 A = 1 A=1。同时说明这个放大器最高可以以 1 MHz 的频率工作而不至于使输入信号失真。由于增益与频率的乘积是确定的,因此当同一器件需要得到 10 倍增益时,它最高只能够以 100 kHz 的频率工作。
单位增益带宽
单位增益带宽定义为:运放的闭环增益为 1 倍条件下,将一个频率可变恒幅正弦小信号输入到运放的输入端,随着输入信号频率不断变大,输出信号增益将不断减小。当从运放的输出端测得闭环电压增益下降 3 dB(或相当于运放输入信号的 0.707)时,所对应的信号频率乘以闭环放大倍数 1 所得的增益带宽积。
导数的运算
因为在高等数学中,我们先学习导数相关运算,再学习积分运算。
简单函数:img
例 1
y = 2 x 3 − 5 x 2 + 3 x − 7 y = 2x^{3}-5x^{2}+3x - 7 y=2x3−5x2+3x−7,求 y ′ y' y′。
解:
y ′ = ( 2 x 3 − 5 x 2 + 3 x − 7 ) ′ = ( 2 x 3 ) ′ − ( 5 x 2 ) ′ + ( 3 x ) ′ − ( 7 ) ′ = 2 ⋅ 3 x 2 − 5 ⋅ 2 x + 3 − 0 = 6 x 2 − 10 x + 3 \begin{align*} y'&=(2x^{3}-5x^{2}+3x - 7)'=(2x^{3})'-(5x^{2})'+(3x)'-(7)'\\ &=2\cdot3x^{2}-5\cdot2x + 3-0=6x^{2}-10x + 3 \end{align*} y′=(2x3−5x2+3x−7)′=(2x3)′−(5x2)′+(3x)′−(7)′=2⋅3x2−5⋅2x+3−0=6x2−10x+3
例 2
f ( x ) = x 3 + 4 cos x − sin π 2 f(x)=x^{3}+4\cos x-\sin\frac{\pi}{2} f(x)=x3+4cosx−sin2π,求 f ′ ( x ) f'(x) f′(x) 及 f ′ ( π 2 ) f'(\frac{\pi}{2}) f′(2π)。
解:
f ′ ( x ) = 3 x 2 − 4 sin x , f ′ ( π 2 ) = 3 4 π 2 − 4 。 \begin{align*} f'(x)&=3x^{2}-4\sin x,\\ f'(\frac{\pi}{2})&=\frac{3}{4}\pi^{2}-4。 \end{align*} f′(x)f′(2π)=3x2−4sinx,=43π2−4。
复合函数: img
例9
设 y = e x 3 y = e^{x^{3}} y=ex3,求 d y d x \frac{dy}{dx} dxdy。
解: y = e x 3 y = e^{x^{3}} y=ex3 可看作由 y = e u y = e^{u} y=eu, u = x 3 u = x^{3} u=x3 复合而成,因此
d y d x = d y d u ⋅ d u d x = e u ⋅ 3 x 2 = 3 x 2 e x 3 \frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}=e^{u}\cdot3x^{2}=3x^{2}e^{x^{3}} dxdy=dudy⋅dxdu=eu⋅3x2=3x2ex3
积分的运算

运放芯片本身需要注意的参数
VOS 输入失调电压
输入失调电压定义为集成运放输出端电压为零时,两个输入端之间所加的补偿电压。输入失调电压实际上反映了运放内部的电路对称性。对称性越好,输入失调电压越小。输入失调电压是运放的一个十分重要的指标,特别是精密运放或是用于直流放大时。输入失调电压与制造工艺有一定关系。例如,双极型工艺(即上述的标准硅工艺)的输入失调电压在 ±1~10 mV 之间。
IB 输入偏置电流
运放两个输入端偏置电流的平均值,确切地说是运算放大器工作在线性区时流入输入端的平均电流。用于衡量差分放大对管输入电流的大小。
IOS 输入失调电流
在零输入时,差分输入级的差分对管基极电流之差, I o s = ∣ I B 1 − I B 2 ∣ I_{os} = |I_{B1} - I_{B2}| Ios=∣IB1−IB2∣。用于表征差分级输入电流不对称的程度。通常, I o s I_{os} Ios 为(0.5~5)nA,高质量的可低于 1 nA。
AOL 开环电压增益
开环电压增益参数 A o l A_{ol} Aol 被定义为输出电压的改变量与两个输入端之间电压改变量之比。
运算放大器的静态输入指标及动态技术指标:输入失调电压、输入失调电流、输入偏置电流、共模抑制比、单位增益带宽、转换速率、压摆率、输入阻抗、输出阻抗。
积分电路的应用:
- 积分电路可以使输入方波转换成三角波或者斜波。
- 积分电路电阻串联在主电路中,电容在干路中。
- 积分电路的时间常数 τ \tau τ 要大于或者等于 10 倍输入脉冲宽度。
- 积分电路输入和输出成积分关系。
积分电压波形
我们经常了解到的方波转为三角波:

如果不增加 R 2 R_2 R2,将会导致输出出现积分饱和,即电容无法放电,导致输出异常甚至可能达到和供电电源一样的电压。因此需要增加这个大的并联电容。
积分电路分析
如果现在施加到 V i n V_{in} Vin 的方波进入其正半周期并在 V i n V_{in} Vin 处产生稳定的正直流电压,则电流将流过 R 1 R_1 R1 并开始对 C 1 C_1 C1 充电。
由于 R 1 R_1 R1 和 C 1 C_1 C1 的交界处的电压(LM324 的反相输入)保持在虚拟地,因此,运放输出(连接至 C 1 C_1 C1 的右端)的电压将开始以一定速率下降,由 C R CR CR 时间常数控制。
输出电压将继续下降,试图达到一个等于 V i n V_{in} Vin 且与 V i n V_{in} Vin 相反的负电压。此动作导致输出端出现相对线性的负向斜率,直到(远在一个时间常数结束之前),输入方波突然改变极性。
在输入方波的负向半周期开始时,将 V i n V_{in} Vin 的电压更改回较低的水平,将导致 C 1 C_1 C1 开始放电,并将反相输入保持在 0V,运算放大器输出的电压将开始以线性方式增加。
这一直持续到下一个周期开始时输入突然再次变为正。
为了在输出三角波形上产生线性斜坡,积分器电路的 C R CR CR 时间常数应类似于或长于输入波周期时间的一半。
在图示的情况下,时间常数 R 1 × C 1 R_1 \times C_1 R1×C1( 100 × 1 0 3 × 10 × 1 0 − 9 100 \times 10^3 \times 10 \times 10^{-9} 100×103×10×10−9)= 220 µs 将周期为 1 / ( 2 × 1 0 3 ) 1 / (2 \times 10^3) 1/(2×103) Hz = 500 µs / 2 = 250 µs 的 1 kHz 方波转换为合理的线性三角波。
反向放大电路并联电容与积分电路并联电阻的区别
By keilzc,2024-05-30 19:30:18
运放反相比例放大电路中反馈电阻两端经常并联一个电容,而运放积分电路的反馈电容上常常并联一个电阻,两者电路结构相似,如下所示(隐去阻容值),二者有何区别呢?电阻、电容分别又起到什么作用?

反相放大电路:电阻为主,电容为辅
先说结论,反相放大电路中,电阻为主,电容为辅,加上电容只是为了让电路更加稳定,避免高频干扰。
从时域角度理解:
我们在 LTspice 中搭建如下仿真电路,输入端 V i n 1 V_{in1} Vin1 模拟一个脉冲干扰,观察输出波形 V o u t V_{out} Vout 会怎样?

简单介绍:输入信号给 1 个激励脉冲,初始电平为 0V,高电平为 1V,1 ms 时刻开始上升,上升时间为 50 ns,高电平维持 50 ns,下降沿 50 ns。电阻 R 1 R_1 R1 为 10 kΩ,电阻 R 2 R_2 R2 为 100 kΩ,反馈电容设置为可变量 C 1 C_1 C1。仿真命令中将 C 1 C_1 C1 设置为列表形式,取值依次为 0 pF 和 2 pF,分别对应没有反馈电容和 2 pF 反馈电容,对应的仿真输出曲线也有两条。
仿真结果如下:

蓝色线为输入信号,模拟 1 个向上的脉冲信号,上升时间为 50 ns,高电平为 1V,维持 50 ns,下降沿 50 ns。
红色线(下面那条, C 1 = 0 C_1 = 0 C1=0 pF)为电容为 0 pF(即没有电容)时的输出,由图可见当没有反馈电容时,输入信号被反向放大 10 倍,幅度达到 -10V。
红色线(中间那条, C 1 = 2 C_1 = 2 C1=2 pF)为电容为 2 pF 时的输出,由图可见当有反馈电容时,输入信号也会被放大。但由于电容两端电压不能突变,输出电压并不是跟随输入立刻达到 -10V,而是缓慢增大。还未达到最大值时,输入信号的脉冲干扰已经消失,此时输出电压不再增加,而是反向减小,恢复原值。与电容滤波原理一样。
电容滤波作用可参考
- 一文彻底讲透电容 【3】—— 电容滤波,不是什么波都能滤的 - 知乎
https://zhuanlan.zhihu.com/p/371762381
下面再来另外一种解释方法,参考
- 运放反馈电阻上并联一个小电容有什么作用?它积分运算放大器上的那个反馈电容一样吗?_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1J94y1R7B8/
个人觉得并不严谨,也可能是自己理解不够。

假设输入信号 V i n V_{in} Vin 有个向上的脉冲干扰,该干扰传递到运放反相输入端,方向向上;而同相输入端接地,电压不变(由于时间很快,还未建立负反馈,因此虚短还未建立,即同相输入端和反相输入端电压并不一致)。由于运放放大作用此时输出端 V o u t V_{out} Vout 有个向下脉冲干扰。但是因为有并联电容 C 1 C_1 C1,电容两端电压不能突变,因此电容右端是缓慢向下变化的,与 LTspice 仿真图中类似。
以上通过仿真和电容知识分析了当有高频干扰时,电容可以起到“缓冲”的作用,减少干扰。
从频域角度理解:
R 2 R_2 R2 和 C 1 C_1 C1 共同组成反馈网络,确切说是“阻抗”,即二者并联值,运放的放大倍数由反馈“阻抗”决定,完整表达式为 R 2 ( 1 + j ω C 1 R 2 ) × R 1 \large\frac{R_2}{(1 + j \omega C_1 R_2) \times R_1} (1+jωC1R2)×R1R2。
对于直流信号而言, ω \omega ω 为 0(反馈电容阻抗 1 j ω C 1 \frac{1}{j \omega C_1} jωC11 无穷大,相当于开路),此时只有反馈电阻 R 1 R_1 R1 有作用,放大倍数退化为 R 2 R 1 \frac{R_2}{R_1} R1R2。
对于高频信号, ω \omega ω 很大(反馈电容阻抗 1 j ω C 1 \frac{1}{j \omega C_1} jωC11 无穷小,相当于短路),放大倍数趋近于 0,即滤除了高频信号,提高运放的稳定性,防止自激震荡。
仿真原理图如下:

简单介绍:幅频特性仿真, R 1 R_1 R1 为 10 kΩ, R 2 R_2 R2 为 100 kΩ,反馈电容设置为可变量 C 1 C_1 C1。仿真命令中将 C 1 C_1 C1 设置为列表形式,取值依次为 0 pF 和 2 pF,对应的仿真输出曲线也有两条。
仿真结果如下:

当反馈电容为 0 pF 时,幅频特性曲线如蓝色线条所示,始终为 20 dB,即放大倍数为 100 k 10 k = 10 \frac{100 k}{10 k} = 10 10k100k=10 倍。
当反馈电容为 2 pF 时,幅频特性曲线如红色线条所示,呈低通滤波特性:低频段为 20 dB,随着频率上升增益下降,-3 dB 大约在 797 kHz,即 1 2 π R 2 C 1 ≈ 795 \frac{1}{2 \pi R_2 C_1} \approx 795 2πR2C11≈795 kHz,理论值与仿真结果一致。
小结
以上为理想运放仿真结果,实际上由于寄生电容的存在,高频干扰更容易造成电路不稳定。因此,为了提高运放的稳定性,防止自激震荡,可以适当增加反馈电容。反馈电容会改变相位并降低带宽,一般都是选 pF 级的电容,即电阻为主,电容为辅。
积分电路:电容为主,电阻为辅
先说结论,运放积分电路中,电容为主,电阻为辅。加上电阻只是为了增加直流通路,避免输入失调电压、输入偏置电流等造成的持续电流使得运放进入饱和状态。
这里贴上《新概念电路》中积分器知识。



《新概念模拟电路》中已经讲得很清楚,我们这里做个仿真,原理图如下:

简单介绍:输入信号 V I N V_{IN} VIN 设置为幅度 1V,频率为 5 kHz 的正弦信号。为了便于计算,电容 C 1 C_1 C1 设置为 3.1831 nF,即在 5 kHz 频率下 10 kΩ 阻抗对应的电容值。运放为理想运放。
仿真结果如下:

红色为输入信号,幅度为 1V,频率为 5 kHz,蓝色为输出信号,幅度也为 1V,频率为 5 kHz,且输出信号明显为输入信号的积分,即该积分电路可正常工作。
上面为理想情况,实际工作中输入信号可能含有直流成分,运放存在失调电压和失调电流,无论哪种情况都会使运放很快进入饱和状态,即输出接近 ± 供电电压。
下面我们调整运放的参数失调电压为 1V(实际一般为 µV 级到 mV 级,此处为了便于显示,修改为 1V),仿真结果如下:

红色为输入信号,交流幅度为 1V,频率为 5 kHz,蓝色为输出信号,趋近于 -15V,即此时处于饱和状态。根据《新概念》,由于存在直流分量,一直对电容充电,此时运放无法维持虚短。图中,灰色线即为运放反相输入端电压,确实不为 0,并没有和同相输入端的 GND 保持一致。
为了使积分电路能正常工作,电容两端并联一个电阻,本次仿真取 100 kΩ,仿真结果如下:

红色为输入信号,交流幅度为 1V,频率为 5 kHz,蓝色为输出信号,均值为 -10V,交流幅度为 1V,频率为 5 kHz。灰色线即为运放反相输入端电压,为 1V,与我们之前设置的失调电压 1V 相等,此时满足虚短。由图可见,输出信号为输入信号的积分,只不过多了个直流分量,相当于积分时的常量。本例中失调电压最终放大了 10 倍,实际使用时失调电压较小,对最终的输出影响也较小。
因此我们可以选取一个合适的电阻值,使积分电路可以正常工作,避免快速进入饱和状态。
也可以换个角度考虑,对于直流信号而言,电容阻抗无穷大,相当于开路,即没有反馈回路,不再满足虚短,那么运放同相输入端和反相输入端的压差肯定会使运放饱和。增加直流反馈通路后,对于直流信号,该电阻可以形成负反馈回路,避免运放饱和。而对于高频信号而言,电容阻抗较小,只要电阻不选得太小,此时并联阻抗取决于电容,电阻也不会影响电路的高频特性。
小结
为了避免积分电路进入饱和状态,需要增益一条直流反馈回路,确保运放工作在“深度负反馈区”,维持运放的虚短特性,此时积分器才可以正常工作。电阻的选取需要根据实际情况进行分析。
积分和微分电路结构原理带 Multisim 仿真
By 永远滴神 yyds,2021-04-08 18:06:57
一、电路与波形
当输入信号流经如图所示的 RC 电路时,因 C C C 的充、放电(延迟)作用,致使输出电压的性质发生了显著变化。积分、微分基本电路即 RC 电路,其积分电路又常做为延时电路应用,延时时间的长短与 R R R、 C C C 值的乘积相关,称为电路的时间常数 τ = R C \tau = RC τ=RC。
如果将 R 1 R_1 R1、 C 1 C_1 C1 互换位置,则变身为微分电路。但电路是否具有积分或微分功能,除了电路的本身结构以外,还需要输入信号 U i U_i Ui 合适才行。
合适的 R C RC RC 电路,再加上合适的 U i U_i Ui 信号。

二、作用及原理
1. 积分电路

-
作用
消减变化量,突出不变量
需要积分电路本身时间常数 τ \tau τ 远大于输入信号的频率周期,即工作当中 C 1 C_1 C1 不会被充满也不可能彻底放完电,输出信号幅度要小于输入信号幅度。电路仅对信号的缓慢变化部分(矩形脉冲的平顶阶段)感兴趣,而忽略掉突变部分(上升沿和下降沿),这是由 R C RC RC 电路的延迟作用来实现的。能将输入矩形波转变成锯齿波(或三角波及其他波形)。
构成积分电路的条件是电路的时间常数 τ ≥ \tau \geq τ≥(输入波形的周期 × 10)
-
原理
RC 电路延迟效应
因 C 1 C_1 C1 两端电压不能突变,在输入信号上升沿至平顶阶段,输入信号经 R 1 R_1 R1 对 C 1 C_1 C1 充电, C 1 C_1 C1 两端电压因充电电荷的逐渐积累而缓慢上升;同样,在输入信号的下降沿及低电平时刻, C 1 C_1 C1 通过 R 1 R_1 R1 放电,其上电压逐渐降低。由 R C RC RC 电路延迟效应,达到了波形变换的目的。在此过程中,因 C 1 C_1 C1 的“迟缓反应”,忽视了信号的突变部分。
2. 微分电路

-
作用
消减不变量,突出变化量
需要电路本身时间常数 τ \tau τ 远小于输入信号的频率周期,即工作当中 C 1 C_1 C1(因其容量特小),充、放电速度极快,输出信号由此会出现双向尖峰(接近输入信号幅度)。电路仅对信号的突变量(矩形脉冲的上、下沿)感兴趣,而忽略掉缓慢变化部分(矩形脉冲的平顶阶段)。微分电路则能将输入矩形波(或近似其他波形)转变为尖波(或其他相近波形)。
输出的尖脉冲波形的宽度与 R × C R \times C R×C 有关(即电路的时间常数), R × C R \times C R×C 越小,尖脉冲波形越尖,反之则宽。此电路的 R × C R \times C R×C 必须远远少于输入波形的宽度,否则就失去了波形变换的作用,变为一般的 RC 耦合电路了。电路的时间常数 τ ≤ \tau \leq τ≤(输入波形周期的 1/10)。
-
原理
电容的充放电
a. 在输入信号上升沿到来瞬间,因 C 1 C_1 C1 两端电压不能突变(此时充电电流最大,电压降落在电阻 R 1 R_1 R1 两端),输出电压接近输入信号峰值(在输出端由耦合现象产生了高电平跳变)。
b. 因电路时间常数较小,在输入信号平顶信号的前段, C 1 C_1 C1 已经充满电, R 1 R_1 R1 因无充电电流流过,电压降为 0V,输出信号快速衰减至 0 电位,直至输入信号下降沿时刻的到来。
c. 下降沿时刻到来时, C 1 C_1 C1 所充电荷经 R 1 R_1 R1 泄放。此时 C 1 C_1 C1 左端相当于接地(构成放电通路),则因电容两端电压不能突变之故,其右端瞬间出现负向最大电平(其绝对值接近输入信号峰值)。
d. C 1 C_1 C1 所充电荷经 R 1 R_1 R1 很快泄放完毕, R 1 R_1 R1 因无充电电流流过,电压降为 0V,输出负向电压信号快速升至 0 电位,直到下一个脉冲的上升沿再度到来。
在此过程中,微分电路取出了输入信号的突变(上升沿与下降沿)部分,对其渐变部分视若无睹。
3. 用途
使用微分和积分电路可以组成无源带通滤波器


三、仿真实例
微分积分电路图
https://download.csdn.net/download/qq_44142969/16554576
运算放大器 (运放) 积分器电路
By 易板,2024-06-21 19:46:42
积分器电路
运算放大器 (运放) 积分器电路是在图 2 运放反相放大器的电路上增加一个积分电容构成,该积分电容并联在运算放大器的反馈电阻上,见图 1。
- 运算放大器 (运放) 反相放大器电路
https://easyboard.blog.csdn.net/article/details/139818400
设计目标
| 输入 f min f_{\min} fmin | 输入 f 0 d B f_{0dB} f0dB | 输入 f max f_{\max} fmax | 输出 V o min V_{o\min} Vomin | 输出 V o max V_{o\max} Vomax | 电源 V c c V_{cc} Vcc | 电源 V e e V_{ee} Vee |
|---|---|---|---|---|---|---|
| 100 Hz | 1 kHz | 100 kHz | -2.45 V | 2.45 V | 2.5 V | -2.5 V |
设计说明
积分器电路根据电路时间常数和放大器的带宽输出某个频率范围上输入信号的积分。会向反相输入施加输入信号,以使输出相对于输入信号的极点反相。理想的积分器电路会根据输入偏移电压的极点在电源轨上饱和,并需要添加一个反馈电阻器 R 2 R_2 R2,以提供稳定的直流运行点。反馈电阻器可限制用于执行积分函数的较低频率范围。该电路最常用作更大反馈 / 伺服环路的一部分,用于提供直流反馈路径,因此无需使用反馈电阻器。
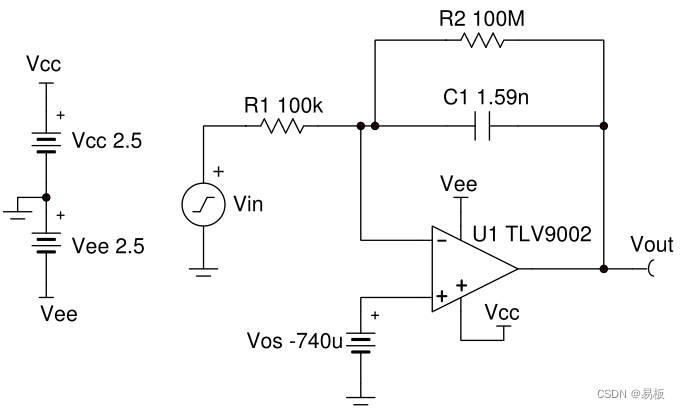
图 1 积分器电路
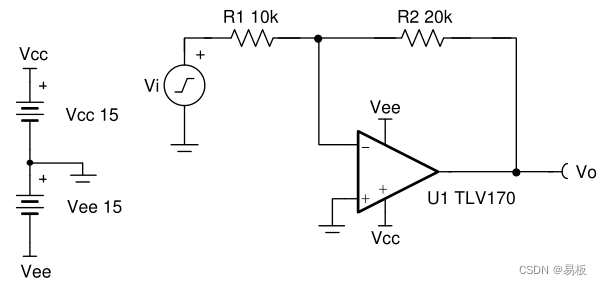
图 2 反相放大器电路
设计说明
-
对于反馈电阻器,所使用的值大小应符合实际。
-
选择一个 CMOS 运算放大器,以最大程度地降低输入偏置电流产生的误差。
-
放大器的增益带宽积 (GBP) 将设置积分函数的频率范围上限。从与放大器带宽相距十倍频的位置开始,积分函数的有效性通常会降低。
-
需要将一个可调节基准连接到运算放大器的同相输入,以抵消输入偏移电压,否则大直流噪声增益将导致电路饱和。具有极低偏移电压的运算放大器可能不需要该操作。
设计步骤
下面给出了理想电路传递函数。
V o u t = − 1 R 1 × C 1 ∫ 0 t V i n ( t ) d t V_{out} = - \frac{1}{R_1 \times C_1} \int_{0}^{t} V_{in}(t) {\mathrm{d}t} Vout=−R1×C11∫0tVin(t)dt
-
将 R 1 R_1 R1 设置为标准值。
R 1 = 100 k Ω R_1 = 100 k\Omega R1=100kΩ
-
计算设置单位增益积分频率所需的 C 1 C_1 C1。
C 1 = 1 2 × π × R 1 × f 0 d B = 1 2 × π × 100 k Ω × 1 k H z = 1.59 n F C_1 = \frac{1}{2 \times \pi \times R_1 \times f_{0dB}} = \frac{1}{2 \times \pi \times 100 k\Omega \times 1 kHz} = 1.59 nF C1=2×π×R1×f0dB1=2×π×100kΩ×1kHz1=1.59nF
-
计算将较低的截止频率设置为比最低工作频率小十倍频所需的 R 2 R_2 R2。
R 2 ≥ 10 2 × π × C 1 × f min ≥ 10 2 × π × 1.59 n F × 10 H z ≥ 100 M Ω R_2 \geq \frac{10}{2 \times \pi \times C_1 \times f_{\min}} \geq \frac{10}{2 \times \pi \times 1.59 nF \times 10 Hz} \geq 100 M\Omega R2≥2×π×C1×fmin10≥2×π×1.59nF×10Hz10≥100MΩ
-
选择增益带宽至少为所需的最大工作频率 10 倍的放大器。
G B P ≥ 10 × f max ≥ 10 × 100 k H z ≥ 1 M H z GBP \geq 10 \times f_{\max} \geq 10 \times 100 kHz \geq 1 MHz GBP≥10×fmax≥10×100kHz≥1MHz
设计仿真
交流仿真结果

积分器电路交流仿真结果
积分器电路瞬态仿真结果
1 kHz 正弦波输入可产生 1 kHz 余弦输出

1 kHz 三角波输入可产生 1 kHz 正弦波输出

1 kHz 方波输入可产生 1 kHz 三角波输出

设计采用的运算放大器 TLV9002
| 参数 | 参数值 |
|---|---|
| V c c V_{cc} Vcc | 1.8V 至 5.5V |
| V i n C M VinCM VinCM | 轨至轨 |
| V o u t Vout Vout | 轨至轨 |
| V o s Vos Vos | 0.4 mV |
| I q Iq Iq | 0.06 mA |
| I b Ib Ib | 5 pA |
| U G B W UGBW UGBW | 1 MHz |
| S R SR SR | 2 V/µs |
| 通道数 | 1、2、4 |
设计备选运算放大器 OPA376
| 参数 | 参数值 |
|---|---|
| V c c V_{cc} Vcc | 2.2V 至 5.5V |
| V i n C M VinCM VinCM | ( V e e − 0.1 V ) (V_{ee} - 0.1V) (Vee−0.1V) 至 ( V c c − 1.3 V ) (V_{cc} - 1.3V) (Vcc−1.3V) |
| V o u t Vout Vout | 轨至轨 |
| V o s Vos Vos | 0.005 mV |
| I q Iq Iq | 0.76 mA |
| I b Ib Ib | 0.2 pA |
| U G B W UGBW UGBW | 5.5 MHz |
| S R SR SR | 2 V/µs |
| 通道数 | 1、2、4 |
真实积分电路设计指南
By 微弱世界,2024-07-29 11:13:02 修改
1 理论积分电路
这个课本上的用于推导积分电路,在实际工程中无法使用,原因如下:
-
偏置电流一直给电容 C 1 C_1 C1 充电。
-
输入失调电压被放大 ∞ \infty ∞ 倍,因为 C 1 C_1 C1 相对直流电压来说短路,阻抗无穷大,导致噪声增益 = 1 + 1/CS / R1 无穷大,运放输出直接饱和。
输入失调电压被放大 ∞ \infty ∞ 倍,因为 C 1 C_1 C1 对于直流而言相当于开路(阻抗 → ∞ \to \infty →∞),导致噪声增益 噪声增益 = 1 + 1 C 1 S R 1 = ∞ \text{噪声增益} = 1 + \frac{1}{C_1 S R_1} = \infty 噪声增益=1+C1SR11=∞,运放输出直接饱和。 ???

电容在直流电路中具有“隔直流,通交流”的特性。在直流电路中,随着时间推移,电容充电完毕后,不再有直流电流通过,此时电容相当于开路,其阻抗趋向于无穷大。所以,从电路原理角度看, C 1 C_1 C1 在直流电路中呈现开路状态,而非短路。 ???
2 解决办法
通过并联电阻 R 2 R_2 R2,改变 VOS 直流信号噪声增益无穷大的情况。这种情况下,噪声增益为 1 + R 2 R 1 \frac{R_2}{R_1} R1R2 = 1 + 100 k 1 k = 101 \frac{100 k}{1 k} = 101 1k100k=101。因此 R 2 R_2 R2 也不能取得太大。

3 并联 R 2 R_2 R2 的影响
与理想积分电路相比,增加 R 2 R_2 R2 后,导致低频段 V F 2 V_{F2} VF2 偏移 V F 3 V_{F3} VF3,不是一个真实的积分器了。但增大 R 2 R_2 R2 后,电路就越像积分器了。同时,噪声增益也变大了。这似乎就相互矛盾了。
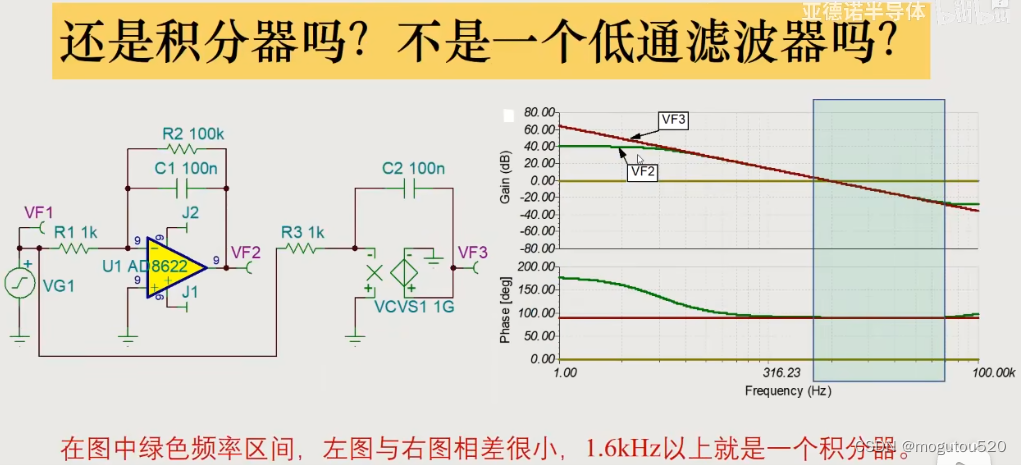

4 设计真实可用积分器


当电阻并联 R 2 R_2 R2 取得足够大时,特征频率 f 0 × 100 < f_0 \times 100 < f0×100< 信号输入频率 f i n f_{in} fin 时,并联 R 2 R_2 R2 后的系统传递函数与理想积分器传递函数相等。

5 实际设计实例
首先必须知道待测信号关键量
- 感兴趣频率范围 f 1 − f 2 f_1 - f_2 f1−f2;
- 待测信号幅度;
- 设计 R 2 R_2 R2。
信号输入频率 f i n > 100 × f 0 f_{in} > 100 \times f_0 fin>100×f0(特征频率),是实用积分器像积分器的关键;
低通特征频率 f 0 = 1 2 π R 2 C 1 < f i n 100 f_0 = \frac{1}{2 \pi R_2 C_1} < \frac{f_{in}}{100} f0=2πR2C11<100fin
R 2 > 100 2 π f i n C 1 R_2 > \frac{100}{2 \pi f_{in} C_1} R2>2πfinC1100,但是 R 2 R_2 R2 不能太大,否则噪声增益会过大,导致失调电压输出偏置过大。
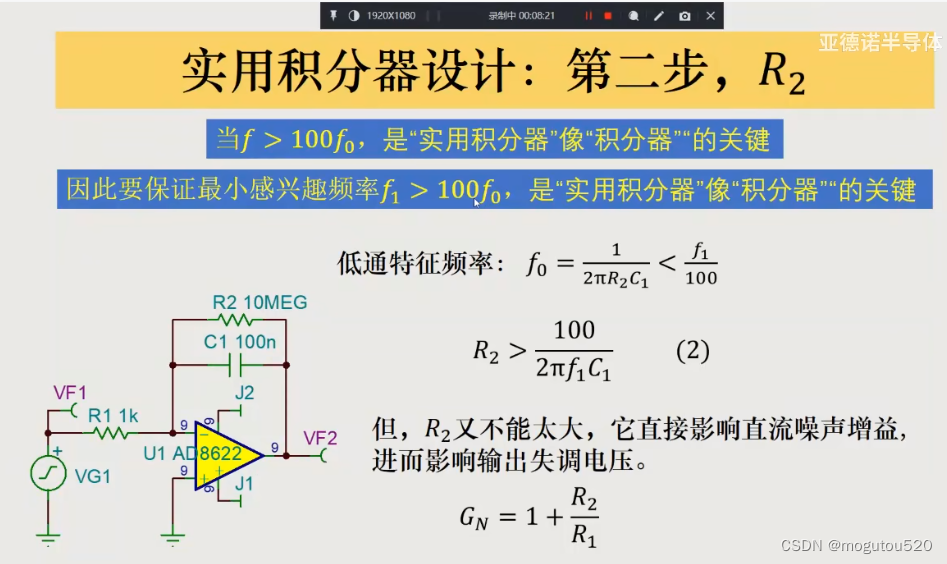
实例设计要求
- 输入信号频率大于 100 Hz。
- 100 Hz 时积分器增益为 6.02 dB。
- 输出失调电压小于 100 mV。
- 使用 AD8622 为核心运放。


详细推导过程

6 真实积分器的问题
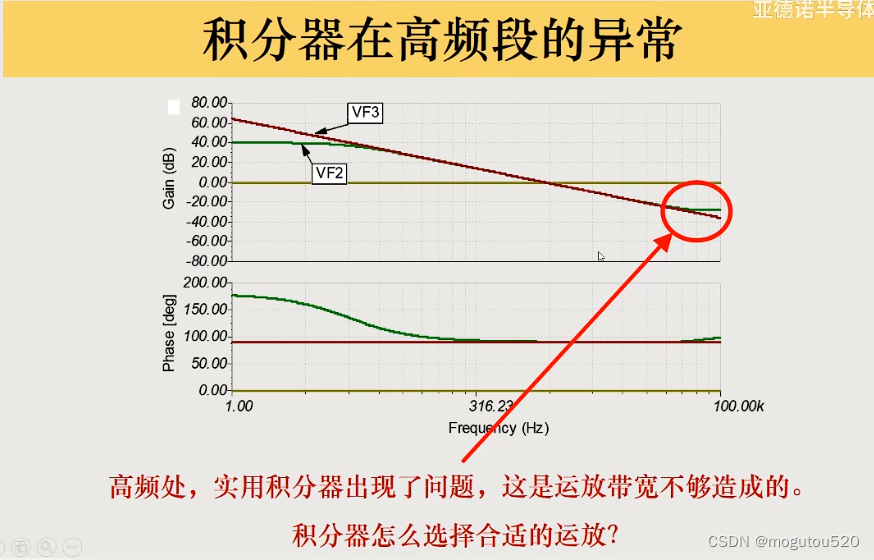
6.1 高频积分异常
运放带宽不够,积分器最高关心的频率为 f H f_H fH,选择运放的 GBP > > >(50~100) × f H \times f_H ×fH。
6.2 方波输入时的输出毛刺
- 运放输出电阻越小,阶跃分压越小,毛刺越小。
- 运放反应越快,越能快速回归,毛刺越小。
- 一般选择高速运放解决上述现象,因为输出电阻一般不好选择。
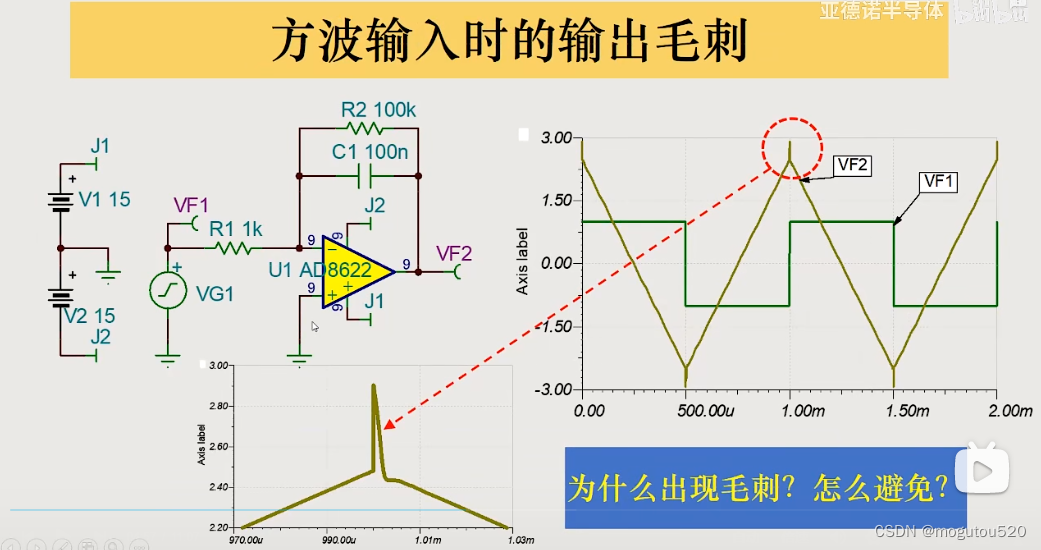
实际验证:
OPA187 增益带宽积为 550 kHz

LMP7701 增益带宽积为 2.5 MHz

6.3 较大直流量输入
当积分器输入信号含直流量,由于积分器的直流增益很大,容易造成输出憋死。此情况下,一般考虑增加隔直电路。
方法一:该方法最大优点是直流噪声增益 = 1。

方法二:可选用大电阻 R 3 R_3 R3,以避免选用大电容,但是这种方法的直流噪声增益仍然很大。

via:
-
RC 电路(积分电路,微分电路)_数电menmenchaigy_新浪博客
https://blog.sina.com.cn/s/blog_710b9b8a0100wmor.html- RC 电路(积分电路,微分电路)详解-CSDN博客
https://blog.csdn.net/GJZGRB/article/details/139667853
- RC 电路(积分电路,微分电路)详解-CSDN博客
-
积分器与微分器简单原理介绍 - qpoling - 博客园
https://www.cnblogs.com/poling777/p/11899931.html -
积分电路和微分电路的工作原理-CSDN博客
https://blog.csdn.net/weixin_42562514/article/details/97653660 -
运算放大器积分电路及积分电路设计_运放积分电路-CSDN博客
https://blog.csdn.net/LUOHUATINGYUSHENG/article/details/105310402 -
积分和微分电路结构原理带Multisim仿真_rc微分电路 multisim-CSDN博客
https://blog.csdn.net/qq_44142969/article/details/115521261 -
反向放大电路并联电容与积分电路并联电阻的区别?_反相运算放大器 要加反馈电容吗-CSDN博客
https://blog.csdn.net/keilzc/article/details/128756648 -
运算放大器(运放)积分器电路_运放积分电路-CSDN博客
https://blog.csdn.net/USALCD/article/details/139868257 -
真实积分电路设计指南-CSDN博客
https://blog.csdn.net/mogutou520/article/details/139467644
