Python----概率论与统计（概率论，互斥事件和概率和，非互斥事件和概率和，独立性事件，生日问题，条件概率）

一、概率论

概率论是研究随机现象的一门数学学科。它为不确定性提供了一个量化的框架，允许我们衡量事件发生的可能性。

概率论研究随机现象，用于量化和分析不确定性。它的基本概念包括：

样本空间（Sample Space）：所有可能结果的集合。

事件（Event）：样本空间的一个子集，通常指我们感兴趣的结果。

概率（Probability）：量化某事件发生的可能性，范围从0到1。

概率是衡量事件发生可能性的指标。

举例：

例如有一颗骰子，它有6个面，随便的扔一下，那么扔到1在上面的概率就是1/6。

或者有一枚硬币，扔到花的一面的概率是1/2或者是50%。不考虑他立起来的情况。

这里的1/6或者1/2就是概率。

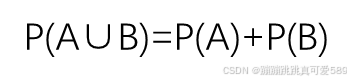
互斥事件（Mutually Exclusive Events）：两个或多个事件不能同时发生。例如，在一次掷骰子中，结果为1和结果为2是互斥的。

概率和公式：如果A和B是互斥事件，则它们的概率和为：P(A∪B)=P(A)+P(B)

例子：

        投掷一枚硬币，A为“正面”，B为“反面”：

        P(A)=0.5

        P(B)=0.5

        P(A∪B)=0.5+0.5=1

非互斥事件（Non-Mutually Exclusive Events）：两个或多个事件可以同时发生。例如，抽取一张牌，A表示“红色”，B表示“面牌”。抽到红色面牌时，A和B同时发生。

概率和公式：对于非互斥事件A和B：P(A∪B)=P(A)+P(B)−P(A∩B)

独立事件（Independent Events）：如果两个事件的发生互不影响，即一个事件的发生并不改变另一个事件发生的概率，那么这两个事件被称为是独立的。

概率计算：如果A与B独立，则：P(A∩B)=P(A)×P(B)

探讨在一群人中，至少有两人生日相同的概率。在23个人中，这个概率超过50%。

条件概率是概率论中的一个基本概念，用于描述在已知某事件发生的情况下，另一个事件发生的概率。换句话说，它是衡量在给定前提条件下，某事件发生可能性的指标。