【动手学深度学习】多层感知机入门
1,多层感知机
在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。 要做到这一点,最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到后面的层,直到生成最后的输出。
最简单的深度网络称为多层感知机。多层感知机由多层神经元组成, 每一层与它的上一层相连,从中接收输入; 同时每一层也与它的下一层相连,影响当前层的神经元。
从本节往后介绍的的模型都属于多层感知机。
2,激活函数
为了发挥多层架构的效力,引入了激活函数如:
Sigmoid、Tanh和ReLU等。激活函数引入了非线性因素,使得网络能够学习和表示非线性关系。
2.1,准备工作
导入模块:
%matplotlib inline
import torch
from d2l import torch as d2l
初始化示例张量:
# 用PyTorch库来创一个一维张量x,元素值从-8.0到8.0(以0.1为步长,元素值不包括8.0)
# 设置requires_grad=True以便在后续计算中记录梯度
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
2.2,ReLU激活函数
ReLU函数是最受欢迎的激活函数,ReLU函数实现简单,表现良好;ReLU函数的数学表达式如下:
- 给定元素x,
ReLU函数被定义为该元素与0中的最大者; - ReLU函数要么让参数消失,要么让参数通过。 这使得优化表现得很好,并且ReLU减轻了困扰以往神经网络的梯度消失问题;
计算并绘制ReLU函数图像:
扫描二维码关注公众号,回复: 17582720 查看本文章
# 应用ReLU激活函数到张量x上,生成了一个新的张量y
y = torch.relu(x)
"""
绘制x和y的关系图:
x.detach() 和 y.detach()从计算图中分离出来的 x 和 y 张量,确保它们不参与梯度计算;
detach() 方法返回一个新的张量,它与原始张量共享数据,但不再要求计算梯度;
'x' 和 'relu(x)':这些是x轴和y轴的名字,用于在绘制的图形中显示;
figsize=(5, 2.5):元组类型,指定了图形宽度为5英寸,高度为2.5英寸;
"""
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
运行结果如下:

计算并绘制ReLU函数的导数图像:
"""
torch.ones_like(x) 可创建一个与 x 形状相同但所有元素都为1的张量。用于指定每个元素的梯度权重;我们想要计算整个 y 关于 x 的梯度,并且没有特别的权重要求,所以使用了全1张量。
对于标量输出,如常见的单个损失函数值,backward() 可以直接调用而无需额外参数,这种情况下,默认梯度是1,即所有路径上的梯度贡献都会被简单地累加起来。
然而,处理非标量输出时。为了正确地计算梯度,必须明确告诉 PyTorch 每个输出元素的重要性或权重。这可以通过传递一个与输出张量形状相同的张量来实现,其中每个元素代表相应输出元素的梯度权重。
显式设置 retain_graph=True,我们可以确保即使在第一次反向传播之后,保留计算图,以便可以再次进行反向传播。因为默认情况下,在backward()被调用后,计算图会被释放以节省内存。
计算y(即ReLU激活函数的输出)关于 x 的梯度。
"""
y.backward(torch.ones_like(x), retain_graph=True)
# x.grad 被填充了 y 关于 x 的梯度值。'grad of relu'是Y轴的标签
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
运行结果如下:

2.2,Sigmoid激活函数
sigmoid函数能够将输入的实数值压缩到0和1之间,因此经常被用作二分类问题的输出层激活函数。sigmoid数学表达式为:
其中, x x x 是输入值, σ ( x ) \sigma(x) σ(x) 是输出值, e e e 是自然对数的底数(约等于2.71828)。
计算并绘制Sigmoid函数的图像:
# torch.sigmoid(x) 用于计算输入张量 x 的Sigmoid激活值,并将结果存储在 y 中
y = torch.sigmoid(x)
# 绘图
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))
运行结果如下:

计算并绘制Sigmoid函数的导数图像:
sigmoid函数的导数为下面的公式:
# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))
运行结果如下:

2.3,Tanh激活函数
与sigmoid函数类似, tanh(双曲正切)函数也能 将其输入压缩转换到特定区间。
tanh函数的输出值被映射到-1和1之间。这意味着,无论输入x取何值,tanh(x)的输出都将落在这个区间内。tanh函数的公式如下:
计算并绘制Tanh函数的图像:
y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))
运行结果如下:
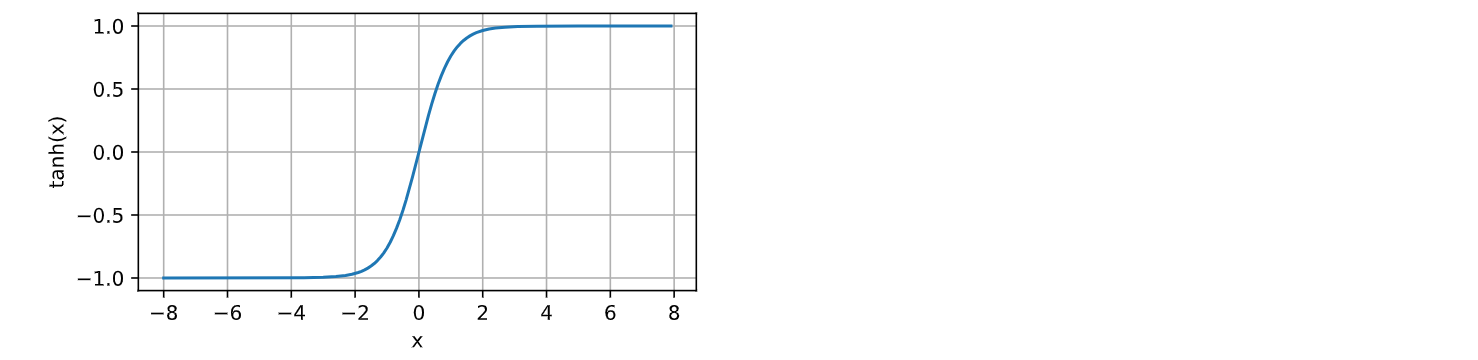
注: Tanh函数的形状类似于sigmoid函数, 不同的是tanh函数关于坐标系原点中心对称。
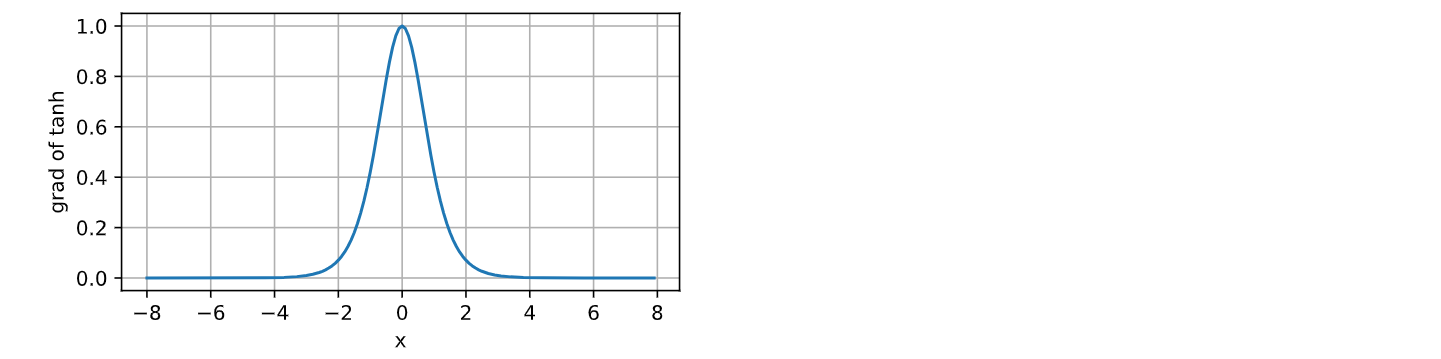
计算并绘制Tanh函数的导数图像:
tanh函数的导数是:
# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))
运行结果如下:
3,简单多层感知机从0开始实现
自己编写函数从0开始实现:使用简单多层感知机进行Fashion-MNIST数据集的图片分类。
3.1,导入模块
导入需要的库
import torch
from torch import nn
from d2l import torch as d2l
3.2,获取数据集
图像分类数据集已在往期文章中介绍(点击链接自取): 【动手学深度学习】Fashion-MNIST图片分类数据集
batch_size = 256
# load_data_fashion_mnist获取一个批量的fashion_mnist数据
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
3.3,初始化模型参数
初始化模型参数,实现一个具有单隐藏层的多层感知机, 它包含256个隐藏单元。
- 回顾一下,Fashion-MNIST中的每个图像由 28×28=
784个灰度像素值组成。 所有图像共分为10个类别; - 对每一层我们都要记录一个权重矩阵和一个偏置向量;
# 输入拉长成一个向量。28*28=784
num_inputs, num_outputs, num_hiddens = 784, 10, 256
# 将生成的随机值乘以 0.01,使得权重值的范围由均值为 0、标准差为 1的随机值缩小到均值为 0、标准差为 0.01 的范围内
# W1 是隐藏层权重,形状为 (784, 256) 的张量
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
# b1表示隐藏层偏置,形状为 (256,) 的张量,初始化为 0
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
# W2 是输出层的权重,形状为 (256, 10) 的张量,初始化为均值为 0、标准差为 0.01 的随机数
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
# b2是输出层的偏置。是一个形状为 (10,) 的张量,初始化为 0
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
3.4,选择激活函数
此处我们自定义一个ReLU函数作为激活函数。
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
3.5,定义模型
定义一个简单的两层全连接的神经网络模型。输入层有 784 个神经元,隐藏层有 256 个神经元,输出层有10个神经元。
def net(X):
X = X.reshape((-1, num_inputs))
# W1 是隐藏层权重,形状为 (784, 256) ,b1表示隐藏层偏置,形状为 (256,)
# W2 是输出层的权重,形状为 (256, 10) ,b2是输出层的偏置。形状为 (10,)
H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法。隐藏层通过矩阵乘法和 ReLU 激活函数进行非线性变换。
return (H@W2 + b2) # 输出层通过矩阵乘法和偏置加法得到每个类别的得分
3.6,选择损失函数
选择交叉熵损失函数作为该模型的损失函数。
loss = nn.CrossEntropyLoss(reduction='none')
3.7,训练模型
多层感知机的训练过程与softmax回归的训练过程完全相同,因此可以直接调用d2l包中softmax处定义的的train_ch3函数。
计算预测正确的样本数
def accuracy(y_hat, y):
# len(y_hat.shape) > 1可判断是否为多维张量,多分类任务中,我们期望 y_hat 是多维的
# y_hat.shape[1]>1 判断列数是否大于1
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
"""
argmax()函数的作用是找出给定轴上最大值的索引;
参数axis=1 指的是沿着每一行进行操作(列通常是0);
找出每一行中最大值元素的索引,存入y_hat,作为预测的分类类别。
"""
y_hat = y_hat.argmax(axis=1)
# dtype()表示求数组或张量中元素的数据类型。此处保证y_hat和y的数据类型一致,以便比较
# cmp最终是一个布尔型张量,存储了y_hat和 y之间元素的比较结果
cmp = y_hat.type(y.dtype) == y
# cmp.type(y.dtype)将cmp的数据类型转换为和y相同,以便可以进行sum操作
# True 转换时可视为 1,False 可视为 0
# 输出的是预测正确的样本数
return float(cmp.type(y.dtype).sum())
计算预测准确率
# 预测正确的样本数除以y长度(样本数)就是预测正确的概率
accuracy(y_hat, y) / len(y)
训练函数
def train_epoch_ch3(net, train_iter, loss, updater):
# 如果使用的是torch.nn.Module实现,则将模型设置为训练模式
if isinstance(net, torch.nn.Module):
net.train()
# 创建一个长度为3的迭代器 。分别记录训练损失总和、训练中正确的样本数、样本数
metric = Accumulator(3)
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer):
# 当updater使用PyTorch内置的优化器时:
# 执行:①梯度清零、②计算梯度、③参数自更新
updater.zero_grad()
"""
反向传播计算平均梯度
"""
l.mean().backward() # 计算平均损失的梯度
"""
step()函数是优化器(torch.optim.Optimizer的子类)的一个方法,用于更新模型的参数。
调用step()时,优化器会根据之前通过反向传播计算得到的梯度来更新模型中的可训练参数
"""
updater.step()
metric.add(float(l.sum()), accuracy(y_hat,y), y.numel())
else: # 使用定制的优化器和损失函数
l.sum().backward()
# 调用自定义更新函数。x是批量大小乘以输入维数的矩阵。X.shape[0]即为批量大小
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
# 返回训练损失和训练精度
return metric[0] / metric[2], metric[1] / metric[2]
迭代训练函数
- num_epochs:训练的总轮数
- updater:优化函数(优化器对象)
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
# Animator用来实现动画效果
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
# train_epoch_ch3 返回的两个值分别是训练损失和训练准确率。train_metrics是个包含两个元素的元组(tuple)
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
# 评估模型在测试集上的精度
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,)) # 绘制动画
# 取出训练损失和训练准确率
train_loss, train_acc = train_metrics
"""
Python的assert语句中,如果条件为False,则后面的值会被转换成字符串形式,用作异常消息
第一个assert语句中的train_loss < 0.5不满足时会抛出一个AssertionError异常,并显示train_loss值作为错误消息
"""
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
训练
# 训练轮数、学习率
num_epochs, lr = 10, 0.1
# 优化器使用小批量随机梯度下降SGD
updater = torch.optim.SGD(params, lr=lr)
# 训练
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
训练结果如下:

定义预测函数
# 定义预测函数
def predict_ch3(net, test_iter, n=6):
for X, y in test_iter: # 从测试数据集迭代器中取出一批次数据(每个批次包含多个图像和对应的标签)
break
# 将真实的数字标签转为文本标签
trues = d2l.get_fashion_mnist_labels(y)
# argmax函数可以找到指定轴上的最大值的索引
# 将预测的数字标签转为文本标签
preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
# 展示六个图像的数据
titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
d2l.show_images(
X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
测试集上应用训练好的模型进行预测:
d2l.predict_ch3(net, test_iter)
预测结果如下(全部预测正确):

4,简单多层感知机的简洁实现
使用深度学习框架来简洁地实现简单多层感知机。与上一节 softmax回归的简洁实现相比, 唯一的区别是我们添加了2个全连接层(之前我们只添加了1个全连接层)。
4.1,定义模型
定义模型
nn.Sequential:是一个容器,用于按顺序包含多个模块。数据会按照在Sequential中模块的顺序传递;nn.Flatten():常用于将多维的输入数据(如图像)转换为一维向量,以便输入到全连接层(nn.Linear)中;输入层:接受 28x28 的图片,展平为 784 维。nn.Linear(784, 256):这是一个全连接层,输入特征数为784,输出特征数为256;nn.ReLU():这是一个激活函数,用于增加网络的非线性;nn.Linear(256, 10):这也是一个全连接层,输入特征数为256,输出特征数为10,即10个类别;
net = nn.Sequential(nn.Flatten(), # 输入层,接受 28x28 的图片,展平为 784 维。
nn.Linear(784, 256), # 隐藏层:256 个神经元,使用 ReLU 激活函数。
nn.ReLU(),
nn.Linear(256, 10)) # 输出层:10 个神经元,对应 10 个类别。
"""
若m为nn.Linear模块,则用nn.init.normal_函数将m的权重初始化为服从均值为0、标准差为0.01的正态分布的随机数。
注意,这里没有显式地初始化偏置(bias),所以偏置将使用默认的初始化方法(通常为零)。
"""
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
"""
net.apply(init_weights):将init_weights函数应用于net中的每个模块。
由于init_weights函数只针对nn.Linear模块执行操作,因此它只会影响net中的全连接层。
"""
net.apply(init_weights);
4.2,训练模型
# 批量大小、学习率、遍历次数
batch_size, lr, num_epochs = 256, 0.1, 10
"""
使用交叉熵损失函数
reduction='none'表示损失函数不会对每个样本的损失进行求和或平均,而是保留每个样本的损失值,这样可以在后续处理中自定义损失的聚合方式(如,对每个批次求平均)
"""
loss = nn.CrossEntropyLoss(reduction='none')
# 使用SGD随机梯度下降,net.parameters()返回神经网络中所有可训练的参数(即权重和偏置)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
# 加载数据
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 训练
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
运行结果如下:
