1.前言

由于受传感器测量误差的影响、SLAM前端处理误差等多个因素的影响，误差是难以避免的，这就产生了“噪声”。后端优化则是对视觉里程计中估计出的相机位姿进行“去噪处理”，也就是对前端视觉里程计估计出的位姿信息进行修正，使其更加精确。后端优化的方法使用比较广泛的是滤波器和非线性优化。VINS后端正是基于优化的方式。

紧耦合系统是将视觉和惯性的原始观测量进行有效的组合，也就是在数据处理前就进行数据融合，及(视觉约束)也加入一起优化。而松耦合的非线性优化就是将视觉约束后计算出的位姿加入到非线性优化中来进行优化。

2.理论推导

1）状态向量
        状态向量共包括滑动窗口内的n+1个所有相机的状态（位置、速度、朝向、加速度bias和陀螺仪bias）、Camera到IMU的外参、m+1个3D点的逆深度：

2)   目标函数

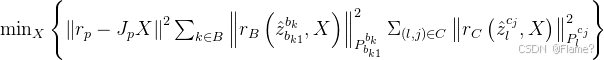
        三个残差项分别是边缘化的先验信息、IMU测量残差、视觉的重投影残差。这三个残差都是用马氏距离来表示的。

        根据《十四讲》中高斯-牛顿法，若要计算目标函数的最小值，可以理解为，当优化变量有一个增量后，目标函数值最小，以IMU残差为例，可写成如下形式：

其中为误差项关于所有状态向量（即优化变量）X的Jacobian，将上式展开并令关于的导数为0，可得增量的计算公式：

        那么，对于整体目标函数的整体增量方程可写成：

上式中为IMU预积分噪声项的协方差，为visual观测的噪声协方差。当IMU的噪声协方差越大时，其信息矩阵将越小，意味着该IMU观测越不可信，换句话说，因IMU噪声较大，越不可信IMU预积分数据，而更加相信visual观测。这里的IMU和visual协方差的绝对值没有意义，考虑的是两者的相对性。

3)   IMU预积分约束

1.残差

        IMU残差为两帧之间的PVQ和bias的变化量的差。

Eigen::Matrix<double, 15, 1> evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
                                      const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
{
    Eigen::Matrix<double, 15, 1> residuals;
    
    Eigen::Matrix3d dp_dba = jacobian.block<3,3>(O_P, O_BA);
    Eigen::Matrix3d dp_dbg = jacobian.block<3,3>(O_P, O_BG);
 
    Eigen::Matrix3d dq_dbg = jacobian.block<3,3>(O_R, O_BG);
 
    Eigen::Matrix3d dv_dba = jacobian.block<3,3>(O_V, O_BA);
    Eigen::Matrix3d dv_dbg = jacobian.block<3,3>(O_V, O_BG);
 
    Eigen::Vector3d dba = Bai - linearized_ba;
    Eigen::Vector3d dbg = Bgi = linearized_bg;
 
    Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
    Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
    Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;
 
    // 残差
    residuals.block<3,1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - P_i - Vi * sum_dt) - corrected_delta_p;
    residuals.block<3,1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
    residuals.block&