【漫话机器学习系列】195.最小二乘法（Ordinary Least Squares, OLS）

最小二乘法（Ordinary Least Squares, OLS）——最经典的线性回归方法

原图来源：Chris Albon
场景：机器学习 / 统计学习 / 回归分析 / 数据建模入门

1. 什么是最小二乘法？

最小二乘法（Ordinary Least Squares, 简称 OLS）是统计学和机器学习中最常见的线性回归方法之一。
它的核心思想非常简单直白：

找一条最合适的直线，使得所有点到这条直线的“垂直距离”的平方和最小。

这条“最合适的直线”其实就是我们想要的模型。

2. 最小二乘法的数学表达式

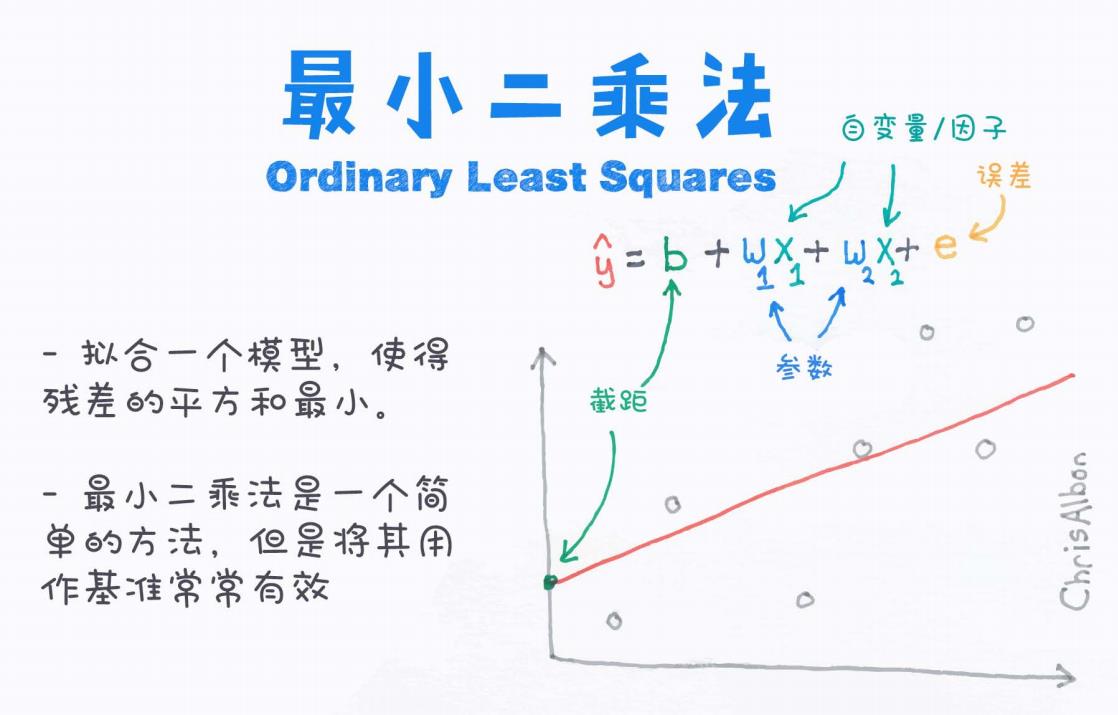
图片中给出了最小二乘法的核心公式：

$\hat{y} = b + w_1x_1 + w_2x_2 + e$

每个符号的含义：

符号	含义
$\hat{y}$	模型预测值（拟合的结果）
b	截距（bias，偏置项）
$w_1, w_2, \dots$	回归系数（参数）
$x_1, x_2, \dots$	自变量（特征、因子）
e	残差（误差，error）

3. 最小二乘法的核心目标

目标是什么？

最小化所有样本的误差平方和（Residual Sum of Squares, RSS）

$RSS = \sum_{i=1}^{n}(y_i - \hat{y_i})^2$

其中：

$y_i$ 是真实值
$\hat{y_i}$ 是预测值
n 是样本个数

这就是最小二乘（Least Squares）的名字来源： → 让残差平方和最小。

4. 最小二乘法的图示理解

图片中用非常直观的图展示了OLS的核心思想：

红色线 → 拟合的直线（预测值）
灰色点 → 真实的数据点
每个点到红色线的距离 → 残差
目标 → 让所有这些残差的平方和尽可能小

5. 最小二乘法为什么有效？

优点：

简单直观
数学基础扎实
计算方便（可直接求解公式）
适合作为建模的起点

适用场景：

自变量和因变量近似线性关系
数据噪声不大
特征维度不高
不存在严重多重共线性

6. 最小二乘法的局限性

局限	影响
对异常值敏感	离群点影响大
对线性假设依赖强	非线性关系拟合效果差
多重共线性问题	自变量之间强相关会影响结果

7. 最小二乘法的演变与扩展

最小二乘法是很多高级回归算法的基础，比如：

方法	思想
岭回归（Ridge Regression）	OLS + L2正则
Lasso回归	OLS + L1正则
ElasticNet	OLS + L1 + L2 正则
广义线性模型（GLM）	OLS 的扩展
多项式回归	构造高阶特征进行拟合

8. 总结

最小二乘法是一种「简单但强大」的算法。
它是理解机器学习回归模型的基础，具有重要的理论与实战意义。

一句话总结：

通过最小化预测值和真实值之间误差的平方和，找到一条最适合数据的线。

9. 附：一句话记忆法

“最小二乘法 = 找到一条直线，让所有点到直线的距离平方和最小”

10. 推荐阅读与拓展

《统计学习方法》李航
《机器学习实战》 Peter Harrington
《ISLR》An Introduction to Statistical Learning
sklearn.linear_model.LinearRegression（Python 实现）