顶刊复现lime(Local Interpretable Model-agnostic Explanations) -可以解释任意模型的机器学习神器

企业开发 2025-04-11 19:29
0 阅读

作者Toby，原文来源公众号Python风控模型，顶刊复现-lime

之前发布文章《顶刊复现-基于机器学习模型的贷款违约可解释预测》，这篇文章用到了lime机器学习可解释性技术。今天Toby老师要复现此论文的lime技术，采用的是银行信贷模型German credit案例。在顶刊lime技术复现中，Toby老师对lime技术做了系统性总结，方便各位用户更好了解lime。

agnostic-机器学习黑箱的不可认知论

在哲学上，"agnostic"（不可知论者）指的是一种认为人类无法或不应该知道关于神或超自然事物的终极真理的观点。不可知论者相信，关于这些主题的知识超出人类的理解能力。

简单模型，比如线性回归和逻辑回归，它们的内部工作机制很透明，我们很容易理解它们是如何做出预测的。然而，当涉及到实际应用时，这些模型的表现往往不如更复杂的模型，比如梯度提升树和神经网络。这些复杂模型虽然预测效果出色，但它们的决策过程不那么透明，难以解释。

目前，许多互联网公司在建模时倾向于使用这些复杂的模型，尽管它们的性能更好，但解释性差的问题一直困扰着业界。因此，模型的可解释性正逐渐成为大家关注的焦点。

LIME概述

图片

Local Interpretable Model-agnostic Explanations（LIME）算法是在2016年由Marco Tulio Ribeiro、Sameer Singh和Carlos Guestrin在论文《“Why Should I Trust You?” Explaining the Predictions of Any Classifier》中提出的。论文链接，https://arxiv.org/abs/1602.04938。

图片


LIME 的目的是提供一种模型无关的解释方法，以帮助理解复杂模型的预测结果。

图片

LIME算支持模型

LIME（局部可解释模型无关解释）支持多种模型的解释，包括：

  • 对结构化模型的解释；

  • 对文本分类器的解释；

  • 对图像分类器的解释；

LIME作为一种解释机器学习模型的工具，使我们能够理解模型为何会做出特定的预测。

众多文章在介绍LIME时，通常强调其在图像和文本识别领域的应用。然而，得益于LIME的模型不可知性（model-agnostic）特点，它同样适用于表格数据的解释。这意味着LIME能够为各种类型的数据集和机器学习模型提供预测解释，不仅限于图像和文本，还包括结构化的表格数据。

图片

上图展示了LIME（Local Interpretable Model-agnostic Explanations）算法在不同图像数据应用场景中的概述：

  1. 第一应用场景：LIME用于分析图像数据，以确定哪些特征影响用户是否购买某个商品。这可能涉及到识别图像中的特定元素或模式，这些元素或模式与用户的购买决策相关。

  2. 第二应用场景：LIME应用于图像识别任务，特别是判断图像是否为猫。这里，LIME帮助解释哪些像素或图像区域是模型用来识别猫的关键因素。

  3. 第三应用场景：LIME用于文本分析，通过图像数据（可能是指文本的可视化表示）来识别哪些关键词或短语用于判断文章的情感倾向。这可能涉及到自然语言处理和情感分析，LIME解释了模型是如何根据文本内容来确定情感极性的。

LIME算法特点


LIME模型的全称清晰地概括了其核心特征：

Local（局部性）表示在目标预测值的邻域内构建一个可解释的模型，该模型在这一点附近的局部表现与复杂模型相似。

Interpretable（可解释性）意味着解释器的模型和特征都必须是易于理解的，能够用局部样本特征来阐释复杂模型的预测结果。

Model-Agnostic（模型无关性）指的是LIME不依赖于复杂模型的具体形式，可以用于解释任何类型的模型。

Explanation（解释性）表明LIME是一种事后解释方法。

下图展示了一个流程图，描述了LIME（Local Interpretable Model-agnostic Explanations）如何与黑盒模型（Black Box Model）协同工作以辅助人类决策的过程。

  1. Data（数据）：流程开始于输入数据。

  2. Black Box Model（黑盒模型）：数据被输入到一个复杂的、不透明的模型中，这个模型被称为黑盒模型，因为它的内部工作机制不易被理解。

  3. Prediction（预测）：黑盒模型处理数据后产生输出，即预测结果。

  4. LIME：LIME算法被应用于这个预测结果。LIME通过在预测结果附近构建一个可解释的模型来提供对黑盒模型预测的解释。

  5. Human Decision（人类决策）：LIME提供的解释帮助人类理解模型的预测，从而做出更加明智的决策。

整个流程图强调了LIME在提高黑盒模型透明度和可解释性方面的作用，以及它如何帮助人类更好地理解和信任机器学习模型的预测。

图片

下图是一个使用LIME（Local Interpretable Model-agnostic Explanations）算法的稀疏线性解释的伪代码。

图片

第一步：获取预测样本周围的随机样本。假设我们有一个预测样本，我们的目标是生成一些与这个样本相似的随机样本，以便在这些样本上模拟和理解原始模型的行为。这些随机样本将用于构建一个局部的、可解释的模型，这个模型将帮助我们解释原始模型的预测。

图片

在它们周围生成N个随机样本

图片

当某一个特征x是类别变量，则根据训练集分布采样，当x为连续变量，新生成的第k个样本的第i个特征为：

图片

其中，a为通过标准正态分布生成的随机数，delta为xi中训练集中的标准差。

第二步：为生成的随机样本打上标签将生成的随机样本放入复杂模型f中训练，得到预测结果。

第三步：计算新生成样本与预测样本的距离随机生成的新样本与预测样本越近，越能更好的解释预测点，因此赋予更高权重。

图片

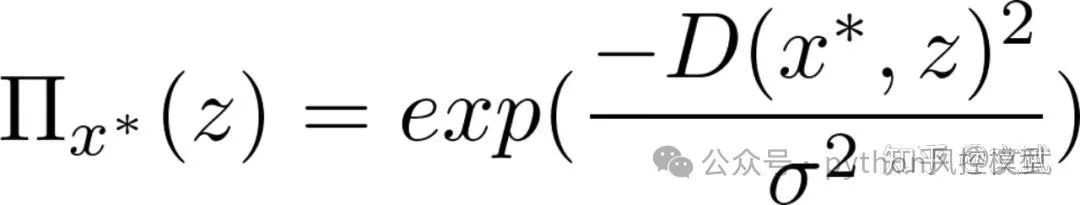
其中，D为距离函数，D越小权重越高。

第四步：构建可解释模型

从p个特征中选部分特征作为解释特征，用于拟合模型。

lime优缺点

LIME算法具有以下优点和缺点：

  1. 通用性强：LIME能够与各种机器学习模型兼容，显示出其广泛的适用性。

  2. 针对性和灵活性：LIME通过选择具有代表性的样本进行训练，减少了工作量并降低了复杂性。它还能够根据客户的特定需求进行定制，例如调整某个特征的权重，以分析该特征变化对结果的影响。

  3. 局部性限制：LIME在局部区域内训练模型以提供解释，但在全局决策过程中，如果存在复杂的非线性关系，LIME可能只能提供有限的解释，因为它的线性模型可能无法捕捉到全局的复杂性。

  4. 高时间成本：在对每个样本进行解释性分析时，LIME需要重新训练一个可解释模型，这可能导致较长的训练时间。

银行信贷预测数据集German credit

"German Credit"（通常被称为德国信贷数据集）是一个经典的数据集，用于银行信贷风险预测模型的研究。这个数据集包含了1000个贷款申请者的记录，每个记录都包含了多个特征，这些特征被用来预测贷款是否会违约。以下是对"German Credit"数据集的概述：

  1. 数据来源：这个数据集最初是由德国帝国银行（Deutsche Bundesbank）提供的，后来被用于机器学习领域的研究。

  2. 特征：数据集包含20个特征，其中包括：

    • 贷款额度

    • 期限

    • 利率

    • 性别

    • 年龄

    • 职业

    • 住房状况（租房、拥有、其他）

    • 信用历史

    • 现有负债

    • 就业状况

    • 婚姻状况

    • 电话号码（是否为电话号码）

    • 邮寄地址（城市、乡村、外国）

    • 住房贷款（是否有住房贷款）

    • 其他贷款（是否有其他贷款）

    • 工作状况（失业、固定工作、临时工作等）

  3. 目标变量：目标变量是二元的，表示贷款是否会违约（1表示违约，0表示未违约）。

  4. 数据预处理：在使用这个数据集之前，通常需要进行一些预处理步骤，如处理缺失值、编码分类变量、特征缩放等。

  5. 应用：这个数据集常用于二分类问题的研究，包括信用评分、风险评估、违约预测等。它被广泛用于测试和比较不同的机器学习算法，如逻辑回归、决策树、随机森林、支持向量机等。

  6. 挑战：这个数据集的挑战在于如何从多个特征中识别出对违约预测最有影响的因素，以及如何处理不平衡数据（违约和未违约的样本数量可能不均衡）。

"German Credit"数据集是机器学习领域中用于教学和研究的宝贵资源，它提供了一个实际的场景来展示和测试信贷风险预测模型。

lime实战German credit

首先我们要读取数据集，然后建立模型

#代码作者QQ：231469242，微信：drug666123
data = pd.read_excel('German_credit.xlsx')
X=data.loc[:,"Account Balance":"Foreign Worker"]
y=data["target"]
train_x, test_x, y_train, y_test=train_test_split(X,y,test_size=0.3,random_state=0)
cb = cb.CatBoostClassifier(eval_metric="AUC")
#cb.fit(train_x,y_train,verbose=False)
eval_dataset=(test_x,y_test)
cb.fit(train_x,y_train,verbose=False,eval_set=eval_dataset)

 
 
然后调用lime解释第1个样本的规则,选择所有20个特征。下图显示好客户概率0.48，坏客户概率0.52，橙色变量为good，蓝色变量为bad。
 
 
 
 
图片
 
 
下图是lime对第一个客户的局部变量解释，我们看大部分变量倾向于good好客户。
 
 
 
 
图片
 
 
 
 
调用lime解释第3个样本的规则,选择20个特征。下图显示好客户概率0.19，坏客户概率0.81，橙色变量为good，蓝色变量为bad。
 
 
 
 
图片
 
 
下图是lime对第3个客户的局部变量解释，我们看大部分变量倾向于bad坏客户。
 
 
 
 
图片
 
 
版权声明：文章来自公众号(python风控模型),未经许可，不得抄袭。遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。 
 



                    
                    

                    
                    

                        
 猜你喜欢

                        

                            

                                
                                
                            

                        

                    

                

            


            
            

                
                

                    
 目录

                    

                        
                    

                


                
                

                    
 热门文章