一文速览DeepSeekMoE：从Mixtral 8x7B到DeepSeekMoE(含MoE架构的实现及DS LLM的简介)

前言

2025年春节期间，deepseek火爆全球——特别是deepseek V3和deepseek R1，其背后的MoE架构引发大量关注，考虑到MoE模型的重要性，特把MoE相关的模型独立成此文

同时因为本文，涉及到了多篇文章的改动，如下表格所示

《从Mistral 7B到MoE模型Mixtral 8x7B的全面解析：从原理分析到代码解读》

《七月论文审稿GPT第3.2版和第3.5版：通过paper-review数据集分别微调Mistral、gemma》

《一文通透DeepSeek V2：详解MoE、Math版提出的GRPO、V2版提出的MLA(改造Transformer注意力)》

《一文速览Gemma 2及其微调：早期paper-7方面review微调Gemma2》

后半部分Mixtral 8x7B 抽取出来，放到本文MoE模型的前半部分

标题变成了《一文速览Mistral 7B及其微调——我司论文审稿GPT第3.2版：微调Mistral 7B instruct 0.2》

$leftarrow$ 微调Mistral部分抽取出来，放到《Mistral 7B文章》中

DeepSeekMoE部分及 DeepSeek LLM部分都放到本文MoE模型中

微调gemma部分放到此文《一文速览Gemma 2及其微调：早期paper-7方面review微调Gemma2》中 $ightarrow$

标题变成了《一文速览Gemma 2及其微调：从论文审稿GPT第3.5版(微调Gemma)，到第5.2版(早期paper-7方面review微调Gemma2)》

相当于标题直接变成了
《一文速览DeepSeekMath及其提出的GRPO：Math模型的三阶段训练方式与群体相对策略优化GRPO》

$leftarrow$ 把此文《一文通透DeepSeek V2：详解MoE、Math版提出的GRPO、V2版提出的MLA(改造Transformer注意力)》的Math版提出的GRPO部分独立成文，放到《七月论文审稿GPT第3.2版和第3.5版》中

第一部分首个开源MoE大模型Mixtral 8x7B

本文的前两部分一开始写于2023年12.23日，当时是属于此文《从Mistral 7B到MoE模型Mixtral 8x7B的全面解析：从原理分析到代码解读》的后半部分

当时的前言是

对于Mixtral 8x7B，OpenAI 团队一直对 GPT-4 的参数量和训练细节守口如瓶。早些时候，有人爆料 GPT-4 是采用了由 8 个专家模型组成的集成系统
后来又有传闻称，ChatGPT 也只是百亿参数级的模型(大概在 200 亿左右)

传闻无从证明，但 Mixtral 8x7B 可能提供了一种「非常接近 GPT-4」的开源选项，特此，本文全面解析下：从原理解析到代码解读(在此文之前，尚没有资料扒得像本文这样如此之细)

1.1 Mixtral 8x7B的整体架构与模型细节

23年12月8日，Mistral AI 在 X 平台甩出一条磁力链接(当然，后来很多人打开一看，发现是接近 87 GB 的种子)

看上去，Mixtral 8x7B的架构此前传闻的GPT-4架构非常相似(很像传闻中GPT-4的同款方案)，但是「缩小版」：

8 个专家总数，而不是 16 名(减少一半)
每个专家为 7B 参数，而不是 166B(减少 24 倍)
47B 总参数（估计）而不是 1.8T(减少 42 倍)
与原始 GPT-4 相同的 32K 上下文

在发布后 24 小时内，已经有开发者做出了在线体验网站：nateraw/mixtral-8x7b-32kseqlen – Run with an API on Replicate

两天后的23年12.11日，Mistral AI团队对外正式发布 Mixtral 8x7B，其在大多数基准测试中都优于 Llama 2 70B，推理速度提高了 6 倍，且它在大多数标准基准测试中匹配或优于 GPT3.5

为免歧义，补充说明下，Mistral AI团队目前总共发布了两个模型

今年10月发布的Mistral 7B
今年12月则发布的混合专家模型，称之为Mixtral 8x7B

特意注意，一个mis 一个mix，本质不同

而Mixtral 8x7B是一个纯解码器模型，下图是Mixtral的核心参数(可以把它和Mistral的核心参数做个对比)

其中前馈块从一组 8 个不同的参数组中进行选择(It is a decoder-only model where the feedforward block picks from a set of 8 distinct groups of parameters)
在每一层，对于每个token，路由器网络(有点类似路径选择器的意思)——也可以称之为门控网络，选择其中的两个组(“专家”)来处理token并通过组合相加得到它们的输出「At every layer, for every token, a router network chooses two of these groups (the “experts”) to process the token and combine their output additively」

相当于从下图的左侧变到了右侧(图源)

这点可能很多朋友不会特别在意，但你仔细品味下，你会发现大有天地，即：每个token 都由某两或三个专家负责完成，最后整个序列则是由一系列「不同的两两专家」组合完成，下文还会详述该点
上下文长度达到32K
Mixtral is pretrained with multilingual data using a context size of 32k tokens

1.1.1 Mixtral 8x7B是一个稀疏的专家混合网络(即Sparse MoE)

如下图所示，传入模型的各个token在经过Attention层及残差连接后，进一步将由路由（Gating/Router）导向2个expert（FFN）中，之后对expert的输出进行加权聚合，再经过残差连接得到当前层的输出

首先，即对于给定的输入 $x$ ，MoE模块的输出由“专家网络输出的加权和”决定，其中权重由“路由/门控网络的输出”确定(The output of the MoE module for a given input x is determined by the weighted sum of the outputs of the expert networks, where the weights are given by the gating network’s output.)

当给定 $n$ 个专家网络 $left{E_{0}, E_{i}, ldots, E_{n-1} ight}$ ，则专家层(expert layer)的输出为：

$sum_{i=0}^{n-1} G(x)_{i} cdot E_{i}(x)$

其中
$ightarrow$ $G(x)_{i}$ 表示第 $i$ 个专家的门控/路由gating网络的n维输出(denotes the n-dimensional output of the gating network for the i-th expert)
$ightarrow$ $E_{i}(x)$ 是第 $i$ 个专家网络的输出(the output of the i-th expert network)
如果门控gating向量稀疏，可以避免计算门为零的专家输出(If the gating vector is sparse, we can avoid computing the outputs of experts whose gates are zero)
且有多种实现G(x)的可选方法，但一种简单且高性能的方法是通过对线性层的Top-K logits进行softmax(but a simple and performant one is implemented by taking the softmax over the Top-K logits of a linear layer [28])
$G(x):=operatorname{Softmax}left(operatorname{TopK}left(x cdot W_{g} ight) ight)$

其中
如果_ $ell_{i}$ 在logits的top-K坐标 $ell in mathbb{R}^{n}$ 中，则 $(operatorname{TopK}(ell))_{i}:=ell_{i}$ ，否则 $(operatorname{TopK}(ell))_{i}:=-infty$ _
_即where $(operatorname{TopK}(ell))_{i}:=ell_{i}$ if $ell_{i}$ is among the top-K coordinates of logits $ell in mathbb{R}^{n}$ and $(operatorname{TopK}(ell))_{i}:=-infty$ otherwise.

举个例子(例子来源于此)，将输入（x）乘以路由器权重矩阵（W）——对应于上面公式中的 $left(x cdot W_{g} ight)$ _

然后，在输出上应用SoftMax来为每个专家创建概率分布G(x)：路由器使用此概率分布为给定的输入选择最佳匹配的专家——对应于上面的公式__ $G(x):=operatorname{Softmax}left(operatorname{TopK}left(x cdot W_{g} ight) ight)$

再其次，将每个选定的专家__G(x)与每个路由器的输出E(x)相乘，并对结果求和——对应于上面的公式 $sum_{i=0}^{n-1} G(x)_{i} cdot E_{i}(x)$ 「注意，一般会选择两个，但下图只选择了一个作为举例」

最后，上述整个流程如下所示「如下图左侧所示，当G(x)的权重结果计算出来后，根据所得权重结果选择4个专家中的最左边那个，然后将G(x)与最左边专家的输出结果E(x)相乘，得到 y，另，如果是两个的话，则G(x)的两个权重分别与4个专家中的某两个做加权求和」
至于每个token所使用的专家数量 $K$ 是可调的参数
当保持 $K$ 不变但增加 $n$ 时，可以增加模型的总参数数量，同时保持计算成本有效不变
The value of K – the number of experts used per token – is a hyper-parameter that modulates the amount of compute used to process each token. If one increases $n$ while keeping $K$ fixed, onecan increase the model’s parameter count while keeping its computational cost effectively constant.

这引出了「总参数数量(通常称为稀疏参数数量)」与用于「处理单个token的活动参数数量」之间的区别
对总参数数量而言，随着 $n$ 的增加而增加；而对于活动参数数量而言， $K$ 直到 $n$ 逐渐增加
This motivates a distinction between the model’s total parameter count (commonly referenced as the sparse parameter count), which grows with n, and the number of parameters used for processing an individual token (called the active parameter count), which grows with K up to n.

说的直白点，如果每个token选择2个专家，则门控网络的权重矩阵计算对应2个专家的权重，比如w1,w2，然后做softmax，最后与2个专家的输出expert1、expert做加权求和
类似
softmax(X × w1)×expert1 +softmax(X× w2)×expert2

其次，如七月官网的「LLM与多模态论文100课程」中一学员所说，关于以上内容的更多细节，可以进一步阅读此论文：Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer

MoE层能够在具备高性能专用内核的单个GPU上高效运行

例如，Megablocks将MoE层的前馈网络(FFN)操作转换为大型稀疏矩阵乘法(Megablocks [13] casts the feed-forward network (FFN) operations of the MoE layer as large sparse matrix multiplications)，从而显著提升了执行速度
并且可以自动处理不同专家被分配可变数量token的情况(naturally handling cases where different experts get a variable number of tokens assigned to them.)

此外，通过标准模型并行技术和一种名为专家并行(EP)的特殊分区策略，MoE层可以在多个GPU上进行分布
Moreover, the MoE layer can be distributed to multiple GPUs through standard Model Parallelism techniques, and through a particular kind of partitioning strategy called Expert Parallelism (EP) [28].

在MoE层执行过程中，旨在由特定专家处理的token会被路由到相应的GPU进行处理，并将专家输出返回到原始token位置
During the MoE layer’s execution, tokens meant to be processed by a specific expert are routed to the corresponding GPU for processing, and the expert’s output is returned to the original token location.

需要注意的是，在负载平衡方面，EP带来了挑战，因为均匀地分配工作负载至关重要以避免单个GPU过载或遇到计算瓶颈
Note that EP introduces challenges in load balancing, as it is essential to distribute the workload evenly across the GPUs to prevent overloading individual GPUs or hitting computational bottlenecks.

进一步，在Transformer模型中，MoE层独立应用于每个token，并替换了Transformer块的前馈(FFN)子块「In a Transformer model, the MoE layer is applied independently per token and replaces the feed-forward (FFN) sub-block of the transformer block」

对于Mixtral

采用与专家函数 $E_{i}(x)$ 相同的SwiGLU架构，并设置K = 2
这意味着每个token被路由到两个具有不同权重集的SwiGLU子块
For Mixtral we use the same SwiGLU architecture as the expert function Ei(x) and set K = 2

综上，输入token $x$ 经过处理后得到输出 $y$ (This means each token is routed to two SwiGLU sub-blocks with different sets of weights)

$y=sum_{i=0}^{n-1} operatorname{Softmax}left(operatorname{Top} 2left(x cdot W_{g} ight) ight)_{i} cdot operatorname{SwiGLU}_{i}(x)$

这个公式类似于GShard架构，不同之处是mixtral用MoE层替换所有FFN子块，而GShard替换所有其他块，并且GShard对分配给每个token的第二个专家使用更详细的门策略

1.1.2Mixtral的参数总量为何是46.7B而非56B

Mixtral 共有 46.7B 个参数，但每个token仅使用 12.9B 个参数。因此，它以与 12.9B 模型相同的速度和相同的成本处理输入并生成输出(Mixtral has 46.7B total parameters but only uses 12.9B parameters per token. It, therefore, processes input and generates output at the same speed and for the same cost as a 12.9B model)

即，虽然Mixtral模型的完整名称为“Mixtral-8x7B-v0.1”，看似有“8x7B=56B”的参数量，但实际的参数量应当是约47B而非56B，因为在各个层中仅有experts部分(FFN)是独立存在的，其余的部分(Attention等)则是各个expert均有共享的
可以想象成一个“纺锤状”的样式，数据由共享模块传输至expert模块对应于纺锤中部发散的部分，对expert的输出进行加权聚合则对应纺锤末端收束的部分

1.1.3Mixtral中所采取的GQA机制

Mixtral沿用了Mistral 7B中所采取的GQA机制，与传统的MHA（Multi-Head Attention）相比，主要是对Attention机制中的K、V表征维度进行控制，从而降低K、V对应的参数量，除GQA外相应地还有MQA（Multi-Query Attention），MQA可以认为是GQA的特例。相关维度如下表所示：

MHA

hidden_dim

GQA

hidden_dim

hidden_dim/n

MQA

hidden_dim

其中n为K和V相对MHA参数量降低的比例，具体地，在Mixtral中n为4

关于GQA的更多细节详见此文《一文通透各种注意力：从多头注意力MHA到分组查询注意力GQA、多查询注意力MQA》

1.1.4Mixtral中的路由(Gating/Router)

路由(Gating/Router)本质是一个线性层，输入维度为隐层维度hidden_dim、输出维度为expert数num_experts。正向传播过程中将被用作预测给定token对应输入各个expert的分值

self.gate = nn.Linear(self.hidden_dim, self.num_experts, bias=False)

至于路由处理的对象可以是Sentence-Level、Token-Level或者Task-Level

Sentence-Level是对各个样本分别进行路由
Token-Level是对样本中的各个token分别进行路由
Task-Level要求不同的expert明确负责不同任务

因此同样也是对各个样本分别进行路由，但其所路由的目标expert是有明确导向的，例如某样本的数据还提供有“所属任务”信息，通过该信息可明确将该样本导向某个专职负责对应任务的expert中

Mixtral采取了Token-Level的处理单位

至于首次在NLP任务中使用Token-Level的MOE可以追溯至2017年的《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》
该论文展示了Token-Level的一些有趣现象，通过观察各个expert所负责token的统计特征，不同的expert确实掌握了一些语法层面理解，当需要不定冠词“a”在重要的动词短语中引入直接宾语时，则会有专门的752号expert来负责输出这个“a”

1.2 模型表现：匹配或超越Llama 2 70B 以及 GPT3.5

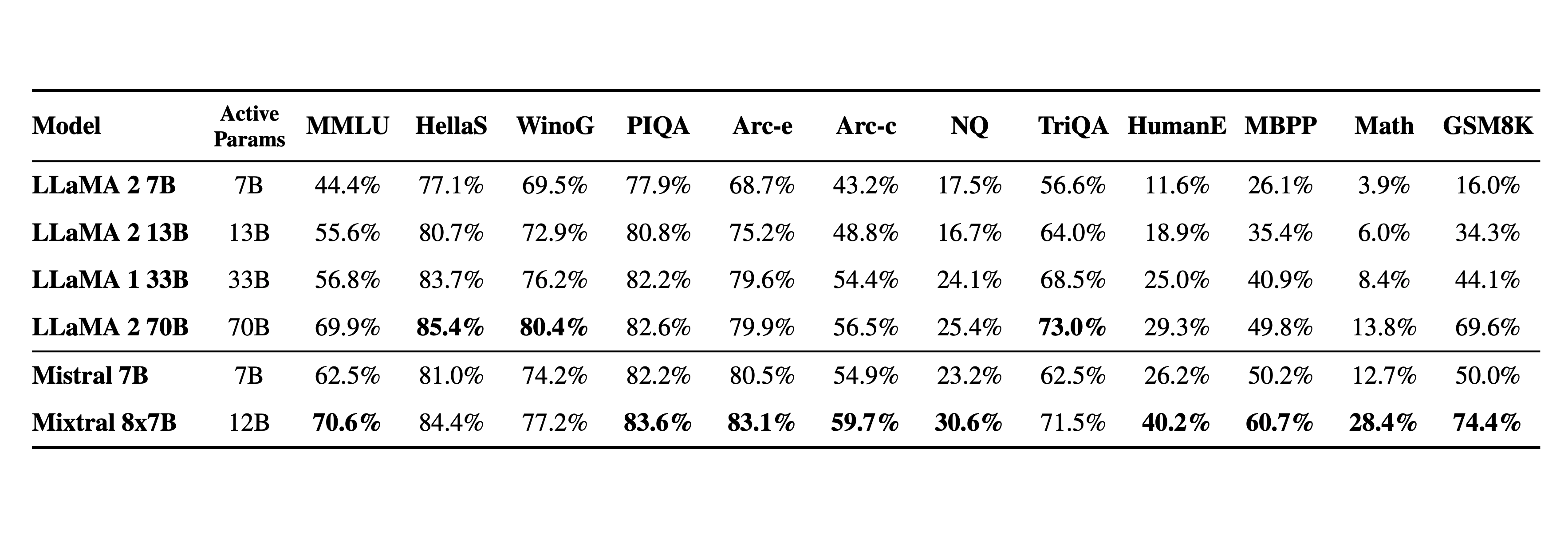
下面将 Mixtral 与 Llama 2 系列和 GPT3.5 基础模型进行比较。Mixtral 在大多数基准测试中均匹配或优于 Llama 2 70B 以及 GPT3.5

性能概览

在下图中的测试，衡量了质量与推理预算的权衡。与 Llama 2 相比，Mistral 7B 和 Mixtral 8x7B 更高效

性能规模

下表给出了上图的详细结果

详细的基准测试

为了识别可能的缺陷，通过微调/偏好建模来纠正，测量了其在BBQ/BOLD 上的性能

BBQ BOLD 基准

与 Llama 2 相比，Mixtral 对 BBQ 基准的偏差较小。总体而言，Mixtral 在 BOLD 上比 Llama 2 显示出更积极的情绪

1.3 指令遵循模型Mixtral 8x7B Instruct

与 Mixtral 8x7B 一起发布还有Mixtral 8x7B Instruct，其在Mixtral 8x7B的基础上通过监督微调和直接偏好优化(DPO)进行优化，以让之严格的遵循指令

关于什么是DPO及其原理细节，请参见此文《RLHF的替代之DPO原理解析：从RLHF、Claude的RAILF到DPO、Zephyr》

在MT-Bench上，它达到了8.30的分数，使其成为最好的开源模型，性能可与GPT3.5相媲美

第二部分Mixtral(MOE架构)的实现细节：代码解读

如阿荀所说(本部分的base版本由我司大模型项目团队第二项目组的阿荀提供，我在其基础上陆陆续续做了大量的补充、说明)，上文中关于mixtral一个比较反直觉的点是：

对于每个token，路由器网络选择其中的两个组(“专家”)来处理token并通过组合相加得到它们的输出「At every layer, for every token, a router network chooses two of these groups (the “experts”) to process the token and combine their output additively」
啥意思，就是如果不仔细了解的话，很容易误以为是“输入的一整个序列”分给TOP 2专家，结果事实是每个token都各自分配TOP 2专家，而且当你仔细抠完mixtral的代码之后，你会发现还真是如此…

2.1 MOE模块的前向传播：整体流程

单个Mixtral层可以大体划分为Attention模块和MOE模块，以下重点关注MOE模块的前向传播过程

2.1.1获取各token对应的top2 expert及其权重

为确保大家可以以最快的速度理解各行代码的含义，我在阿荀分析的基础上拆成了以下六个步骤，且对每个步骤都加了额外的解释说明

由于hidden_states的维度，通常包括批大小(batch_size)、序列长度(sequence_length)和隐藏层维度(hidden_dim)，故有
```
# 由Attention模块输出的hidden_states作为本部分的输入
batch_size, sequence_length, hidden_dim = hidden_states.shape
```

将hidden_states的形状重构为一个二维张量，用于将其处理为每个token的表示

# 转换成(bs*seq_len, hidden_dim)，即token-level
hidden_states = hidden_states.view(-1, hidden_dim)

通过一个门控(gate)机制来生成路由逻辑(router_logits)，用于后续决定每个token应由哪些专家(experts)处理
```
# router_logits: (batch * sequence_length, n_experts)
# (bs * seq_len, n_experts)
router_logits = self.gate(hidden_states)
```

对每个token的路由逻辑应用softmax函数，计算每个专家对每个token的处理权重

# 在token-level（dim=1）进行softmax，即每个token都各自进行n_experts分类的输出
routing_weights = F.softmax(router_logits, dim=1, dtype=torch.float)

选取每个token的前top_k个最重要的专家及其权重

# routing_weights: (bs * seq_len, topk)，是选取的experts对应的原始权重
# selected_experts: (bs * seq_len, topk)，是选取的experts的编号/索引号
routing_weights, selected_experts = torch.topk(routing_weights, self.top_k, dim=-1)

对选出的每个token的专家权重进行归一化处理，确保每个token的专家权重之和为1

# 对原始权重重新归一化，使得所取出的experts权重加和等于1
# routing_weights的具体样例见下文的【代码块A】
routing_weights /= routing_weights.sum(dim=-1, keepdim=True)

2.1.2将各token传入对应的expert模型中进行前向传播得到输出

首先

# final_hidden_states: (bs * seq_len, hidden_dim)
# 由全0张量初始化
# final_hidden_states将用于存储各token对应expert的聚合结果
final_hidden_states = torch.zeros(
    (batch_size * sequence_length, hidden_dim), dtype=hidden_states.dtype, device=hidden_states.device
)

根据给定的selected_experts作为元素1所在位置的索引，构建向量长度为num_experts的one-hot编码
好比24个token，需要由8个expert两两组合处理，那我针对每一个token都构建长度为8的0 1编码，这个编码分别代表8个expert
故，每个token选择了哪两个expert，则对应的编码位上变为1，否则为0

比如July这个token选择3 7两个expert，则July对应的0 1编码位：0 0 1 0 0 0 1 0
再比如Edu这个token如果选择了2 4两个expert，则其01编码为：0 1 0 1 0 0 0 0
依此类推…
```
# selected_experts.shape: (bs*seq_len, topk)
# torch.nn.functional.one_hot(selected_experts, num_classes=self.num_experts).shape: (bs*seq_len, topk, num_experts)
```
使用相对取巧方法来进行前向传播
```
expert_mask = torch.nn.functional.one_hot(selected_experts, num_classes=self.num_experts).permute(2, 1, 0)
```
具体而言，下面这个张量
torch.nn.functional.one_hot(selected_experts, num_classes=self.num_experts).permute(2, 1, 0).shape: (num_experts, topk, bs*seq_len)
的物理含义是由“每个token分别选取了哪topk个expert”变成了“每个expert分别作为各个排位存在的时候，对应需要处理哪些token”
这样做的好处在于：后续循环的时候只需要进行num_experts次前向传播就能得到结果，而无需进行bs*seq_len次前向传播

为方便大家更好的理解上面那行代码的含义，我特地画了个示意图以加快理解
$ightarrow$ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z，是需要处理的token
$ightarrow$ 1 2 3 4 5 6 7 8，代表8个expert
(如阿荀所说，如此，便把关注视角从“各个token”变成了“各个专家”，当然，大部分情况下 token数远远不止下图这5个，而是比专家数多很多。总之，这么一转换，最终可以省掉很多循环)

所以接下来只需要进行num_experts次循环

# 根据次序逐个取出expert模型
for expert_idx in range(self.num_experts):
    expert_layer = self.experts[expert_idx]
    idx, top_x = torch.where(expert_mask[expert_idx])

上面这几行代码得好好解释下
$ightarrow$ 由于_expert_mask_记录有各个expert分别作为各个排位存在的时候，对应需要处理哪些token，故_expert_mask[expert_idx].shape: (topk, bs*seq_len)_，便是从expert_mask中取出其对应的，详见下文的【3.2.2 代码块B：expert_mask[expert_idx]】

$ightarrow$ 上面三行的最后一行中等式中的右边项：torch.where(expert_mask[expert_idx])，则是辨析出_expert_mask[expert_idx]_值为1的位置索引，详见下文的【3.2.3 代码块C：idx, top_x = torch.where(expert_mask[expert_idx])】

$ightarrow$ 至于：idx.shape: (bs * seq_len, )，则代表expert_mask[expert_idx]中(每列)元素值为1的索引位置
以及：top_x.shape: (bs * seq_len, )，则代表expert_mask[expert_idx]中(每行)元素值为1的索引位置

继续分析该for循环之后的代码，如下

    # 如果exert_mask[expert_idx]不存在元素为1的值则跳过
    if top_x.shape[0] == 0:
        continue

    # 全部token的隐向量hidden_states中取出当前expert对应token的隐向量
    # current_state.shape: (top_x_length, hidden_dim)
    current_state = hidden_states[None, top_x_list].reshape(-1, hidden_dim)

    # 将取出的token隐向量传入expert模型进行前向传播得到返回
    # current_hidden_states.shape: (top_x_length, hidden_dim)
    # expert_layer的正向过程详见下文的【3.2.4 代码块D：expert内部的前向传播】
    current_hidden_states = expert_layer(current_state, routing_weights[top_x_list, idx_list, None])

    # 将当前expert的输出以加和的形式写入预先定义好的final_hidden_states张量中
    final_hidden_states.index_add_(0, top_x, current_hidden_states.to(hidden_states.dtype))

for循环结束后，相当于所有expert均处理完毕后，将维护好的_final_hidden_states_由(bs * seq_len, hidden_dim)转为(bs, seq_len, hidden_dim)，并将作为本批次运行的返回
更多详见下文的【3.2.5 代码块E：final_hidden_states】
```
final_hidden_states = final_hidden_states.reshape(batch_size, sequence_length, hidden_dim)
```

3.2 MOE前向传播中五个代码块的细致分析：鞭辟入里

3.2.1代码块A：routing_weights的具体样例

# 【代码块A】routing_weights
# 每行对应1个token，第0列为其对应排位第1的expert、第1列为其对应排位第2的expert，元素值为相应权重
[[0.5310, 0.4690],
 [0.5087, 0.4913],
 [0.5775, 0.4225],
 [0.5014, 0.4986],
 [0.5030, 0.4970],
 [0.5479, 0.4521],
 [0.5794, 0.4206],
 [0.5545, 0.4455],
 [0.5310, 0.4690],
 [0.5294, 0.4706],
 [0.5375, 0.4625],
 [0.5417, 0.4583],
 [0.5014, 0.4986],
 [0.5239, 0.4761],
 [0.5817, 0.4183],
 [0.5126, 0.4874]]

3.2.2 代码块B：expert_mask[expert_idx]

因为有：expert_mask记录有各个expert分别作为各个排位存在的时候，对应需要处理哪些token
故而有：expert_mask[expert_idx]从expert_mask中取出第expert_idx个expert将处理哪些token
$ightarrow$ 第0行为该expert作为排位第1存在的时候处理的token
$ightarrow$ 第1行为该expert作为排位第2存在的时候处理的token

# 【代码块B】expert_mask[expert_idx]
# 下述两行例子的物理含义为：
# 第一行是“该expert作为排位1的exert存在时，需要处理第9个token；
# 第二行是“该expert作为排位2的expert存在时，需要处理第10、11个token”
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]]

3.2.3 代码块C：idx, top_x = torch.where(expert_mask[expert_idx])

# 【代码块C】idx, top_x = torch.where(expert_mask[expert_idx])
# 以上述expert_mask[expert_idx]样例为例，对应的torch.where(expert_mask[expert_idx])结果如下
idx: [0, 1, 1]
top_x: [9, 10, 11]

idx对应行索引，top_x对应列索引，例如张量expert_mask[expert_idx]中，出现元素1的索引为(0, 9)、(1, 10)、(1, 11)
从物理含义来理解，top_x实际上就对应着“关乎当前expert的token索引”，第9、第10、第11个token被“路由”导向了当前所关注的expert，通过top_x可以取到“需要传入该expert的输入”，也即第9、第10、第11个token对应的隐向量

因此top_x将作为索引用于从全部token的隐向量hidden_states中取出对应token的隐向量
而idx和top_x也会组合起来被用于从expert权重张量routing_weights中取出对应的权重

并且通过行索引、列索引的组合routing_weights

3.2.4 代码块D：expert内部的前向传播

# 【代码块D】expert内部的前向传播
def forward(self, hidden_states, routing_weights):
    current_hidden_states = self.act_fn(self.w1(hidden_states)) * self.w3(hidden_states)
    current_hidden_states = self.w2(current_hidden_states)
    return routing_weights * current_hidden_states

其入参不仅有expert相应token的隐向量，还有对应expert的权重，整体是一个基于swiGLU激活的FFN

最后对FFN的输出进行加权得到该expert的实际输出，因此加权处理是在expert的内部就已经进行了

3.2.5 代码块E：final_hidden_states

最初final_hidden_states是全0张量

# 查看与当前expert有关的final_hidden_states部分，即final_hidden_states[top_x]
[[0., 0., 0., ?..., 0., 0., 0.],
?[0., 0., 0., ?..., 0., 0., 0.],
?[0., 0., 0., ?..., 0., 0., 0.]]

使用.index_add_函数后在指定位置(top_x)加上了指定值(current_hidden_states)

final_hidden_states.index_add_(0, top_x, current_hidden_states.to(hidden_states.dtype))

再次查看与当前expert有关的final_hidden_states部分，即

[[ 0.0938,  0.0509, -0.0689,  ..., -0.0182, -0.0246,  0.0468],
 [ 0.1246,  0.0642,  0.0015,  ...,  0.0100, -0.0110,  0.0219],
 [ 0.0478, -0.0192,  0.0139,  ..., -0.0039, -0.0197,  0.0475]]

以上两部分的参考文献与推荐阅读，如下所示

一条磁力链接席卷AI圈，87GB种子直接开源8x7B MoE模型

Mistral AI对Mixtral of experts的介绍：Mixtral of experts | Mistral AI | Open source models

开源大模型超越GPT-3.5！爆火MoE实测结果出炉

replicate-examples/mixtral at main · nateraw/replicate-examples · GitHub

预训练大模型：百度UFO(Unified Feature Optimization)

集4学员且友人wstart推荐的三篇论文
LoRAMoE: Revolutionizing Mixture of Experts for Maintaining World Knowledge in Language Model Alignment
MegaBlocks: Efficient Sparse Training with Mixture-of-Experts
Weak-to-Strong Generalization: Eliciting Strong Capabilities With Weak Supervision

Mixtral 8x7B论文终于来了：架构细节、参数量首次曝光
 一条磁力链爆全网，Mixtral 8x7B论文来了！碾压Llama 2 70B，每token仅需激活13B参数

Mixtral of Experts论文，是本文中此节“1.1.1 Mixtral 8x7B是一个稀疏的专家混合网络”的核心参考

图解Mixtral 8 * 7b推理优化原理与源码实现

第三部分 DeepSeekMoE的创新：细粒度专家分割与共享专家隔离(含DeepSeek LLM的详解)

3.1DeepSeek LLM(7B、67B)的预训练与对齐

3.1.1 架构设计、预训练、并行训练等细节

24年1.5日，量化巨头幻方旗下的杭州深度求索公司提出DeepSeek LLM，其对应的论文为《DeepSeek LLM: Scaling Open-Source Language Models with Longtermism》

该模型基本遵循Llama结构的设计「关于llama结构的解读，详见此文：LLaMA的解读与其微调(含LLaMA 2)：Alpaca-LoRA/Vicuna/BELLE/中文LLaMA/姜子牙__」
比如采用了RMSNorm函数的Pre-Norm结构，并使用SwiGLU作为前馈网络FFN的激活函数，中间层的维度为 $rac{8}{3} d_{ ext {model }}$ ，它还结合了旋转嵌入RoPE作为位置编码
且为了优化推理成本，67B 模型使用了分组查询注意力GQA「如上文提到过的，关于GQA的更多细节详见此文《一文通透各种注意力：从多头注意力MHA到分组查询注意力GQA、多查询注意力MQA》」，而不是传统的多头注意力MHA

此外，DeepSeek LLM 7B 是一个30层的网络，而 DeepSeek LLM 67B 有95层，更多参数如下表所示

以下是其他的一些细节

基于tokenizers库(Huggingface团队，2019)实现了字节级字节对编码(BBPE)算法
DeepSeek LLM 以0.006的标准差初始化，并使用 AdamW 优化器进行训练，具有以下超参数： ??1 = 0.9, ??2 = 0.95, 和 weight_decay = 0.1
在预训练期间，采用了多步学习率调度器(multi-step learning rate scheduler)，而不是典型的余弦调度器
原因在于当在保持模型大小不变的情况下调整训练规模时，多步学习率调度器允许重用第一阶段的训练，从而为持续训练提供了独特的便利，因此，选择了多步学习率调度器作为默认设置

具体来说，模型的学习率在2000个预热步骤后达到最大值，然后在处理80%的训练数据后下降到最大值的31.6%。在处理90%的数据后，它进一步减少到最大值的10%

此外，在模型的加速上

使用一个名为 HAI-LLM的高效轻量级训练框架来训练和评估大型语言模型
让数据并行、张量并行、序列并行和1F1B流水线并行被集成到这个框架中，就像在Megatron中所做的那样「_如果还不太熟悉并行训练相关的原理，可以参见此文：**大模型并行训练指南：通俗理解Megatron-DeepSpeed之模型并行与数据并行(含ZeRO优化)**_」

且还利用了flash attention「关于flash attention，详见此文《通透理解FlashAttention(含其2代和第3代)：全面降低显存读写、加快计算速度》」来提高硬件利用率，以及利用ZeRO-1将优化器状态划分到数据并行等级中
还努力重叠计算和通信以最小化额外的等待开销，包括最后一个微批次的反向过程和ZeRO-1中的reduce-scatter操作，以及序列并行中的GEMM计算和all-gather/reduce-scatter
一些层/操作被融合以加速训练，包括LayerNorm、GEMM和Adam更新
为了提高模型训练的稳定性，在 bf16 精度下训练模型，但在 fp32 精度下累积梯度
为了减少 GPU 内存消耗，执行就地交叉熵操作，即：在交叉熵 CUDA 内核中即时将 bf16 logits 转换为fp32 精度（而不是事先在 HBM 中转换），计算相应的 bf16 梯度，并用其梯度覆盖 logits

且模型权重和优化器状态每 5 分钟异步保存一次，这意味着在偶尔的硬件或网络故障的最坏情况下，最多会丢失 5 分钟的训练数据。这些临时模型检查点会定期清理，以避免消耗过多的存储空间

且还支持从不同的 3D 并行配置恢复训练，以应对计算集群负载的动态变化。
至于评估，在生成任务中采用 vLLM (Kwon et al., 2023)，在非生成任务中采用连续批处理，以避免手动调整批处理大小并减少 token 填充

3.1.2 对齐：监督微调与DPO

在数据集上，收集了大约 150 万条英文和中文的指令数据实例，涵盖了广泛的有用性和无害性主题。其中

有用数据包含 120 万个实例，其中 31.2% 是一般语言任务，46.6% 是数学问题，22.2% 是编码练习
安全数据包含 30 万个实例，涵盖各种敏感话题

至于对齐流程则包含两个阶段

监督微调
对 7B 模型进行了 4 个周期的微调，但对 67B 模型只进行了 2 个周期的微调，因为观察到 67B 模型的过拟合问题很严重
且观察到 GSM8K和 HumanEval在 7B 模型上持续改进，而 67B 模型很快达到了上限
对于 7B 和 67B 模型，它们对应的学习率分别为 1e-5 和 5e-6

除了监控基准准确性外，我们还评估了微调过程中聊天模型的重复率
比如，收集了总共 3868 个中英文提示，并确定了生成的响应中未能终止而是无休止重复一段文本的比例
且观察到，随着数学 SFT 数据量的增加，重复率往往会上升，这可以归因于数学 SFT 数据偶尔包含类似的推理模式。因此，较弱的模型难以理解这些推理模式，导致重复的响应

为了解决这个问题，尝试了两阶段微调和 DPO「关于什么是DPO，详见此文：RLHF的替代之DPO原理解析：从RLHF、Claude的RAILF到DPO、Zephyr__」，这两种方法几乎都能保持基准分数并显著减少重复
DPO
为了进一步增强模型的能力，他们使用了直接偏好优化算法DPO，这被证明是一种简单但有效的 LLM 对齐方法

比如构建了DPO训练的偏好数据，主要包括有用性和无害性
$ightarrow$ 对于有用性数据，收集了多语言提示，涵盖了创意写作、问答、指令执行等类别，然后使用DeepSeek Chat模型生成响应作为候选答案
$ightarrow$ 类似的操作也应用于无害性偏好数据的构建
且以5e-6的学习率和512的批处理大小训练了一个DPO周期，并使用了学习率预热和余弦学习率调度器
另，发现DPO可以增强模型的开放式生成能力，同时在标准基准测试中的表现差异很小

3.2DeepSeekMoE(16B)的创新：细粒度专家分割与共享专家隔离

3.2.1 为何提出细粒度专家分割和共享专家隔离

24年1.11日，深度求索公司很快又提出了DeepSeekMoE，其对应的论文为《DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models》

在参数规模上，虽然只有16B(在2T的token数据上训练而成)，但由于其性能的高效，使得其达到同等的性能下，所需要调动的参数量是相比其他模型更低的，如下图所示

那DeepSeekMoE到底有什么创新性呢？

首先，传统的 MoE 架构用 MoE 层替代了 Transformer 中的前馈网络 (FFNs)。每个 MoE 层由多个专家组成，每个专家在结构上与标准 FFN 相同，每个token被分配给一个或两个专家

这里面存在两个问题

在专家数量有限的情况下，分配给特定专家的token更有可能涵盖多种类型的知识
因此，指定的专家将倾向于在其参数中学习截然不同类型的知识，而这些知识难以同时利用
然而，如果每个token可以被路由到更多的专家，分散的知识将有可能在不同的专家中分别学习

有些知识是比较大众通用的，所以会导致某几个专家会被调用的异常频繁

那是否可以比较好的解决这两个问题呢

对于前者，DeepSeekMoE提出细粒度专家分割——Fine-Grained Expert Segmentation：在保持参数数量不变的情况下，通过拆分FFN 中间隐藏维度来将专家分割为更细的粒度(说白了，细粒度的专家分割允许将多样化的知识更精细地分解，并更精确地学习到不同的专家中，从而使得专家更专业)

相应地，在保持计算成本不变的情况下，还激活了更多细粒度的专家，以实现更灵活和适应性更强的激活专家组合(增加的激活专家组合的灵活性也有助于更准确和有针对性的知识获取)
对于后者，DeepSeekMoE提出共享专家隔离——Shared Expert Isolatio：隔离某些专家作为共享专家，这些专家始终被激活，旨在捕捉和巩固不同上下文中的共同知识

综上，如下图所示(子图a展示了具有传统 top-2 路由策略的 MoE 层；子图b说明了细粒度专家分割策略；随后，子图c展示了共享专家隔离策略的集成，从而构成了完整的 DeepSeekMoE 架构）

3.2.2 前情回顾：基于transformer的传统MoE结构

注，本节只是简单梳理回顾，如有疑问，可以再详细看下上文的第一部分

一个标准的Transformer语言模型是通过堆叠 ??层标准的Transformer块构建的，每个块可以表示如下(为简洁起见，省略了层归一化)

$egin{aligned} mathbf{u}_{1: T}^{l} & =operatorname{Self}-operatorname{Att}left(mathbf{h}_{1: T}^{l-1} ight)+mathbf{h}_{1: T}^{l-1} \ mathbf{h}_{t}^{l} & =operatorname{FFN}left(mathbf{u}_{t}^{l} ight)+mathbf{u}_{t}^{l} end{aligned}$

其中

$T$ 表示序列长度
$mathbf{u}_{1: T}^{l} in mathbb{R}^{T imes d}$ 表示第 $l$ 层注意力模块的所有token的隐藏状态
$mathbf{h}_{t}^{l} in mathbb{R}^{d}$ 是第 $l$ 层transformer块后第 $t$ 个token的输出隐藏状态

构建 MoE 语言模型的典型做法通常是在指定的间隔处用 MoE 层替换 Transformer 中的 FFN

MoE 层由多个专家组成，每个专家在结构上与标准 FFN 相同
然后，每个token将被分配给一个或两个专家
如果将第 $l$ 个 FFN 替换为 MoE 层，则其输出隐藏状态 $mathbf{h}_{t}^{l}$ 的计算表示为

其中

$N$ 表示专家的总数
$mathrm{FFN}_{i}(cdot)$ 是第 $i$ 个专家的FFN
$g_{i, t}$ 表示第 $i$ 个专家的门控值
$S_{i, t}$ 表示token到专家的亲和度
$operatorname{Topk}(cdot, K)$ 表示第 $t$ 个token和所有 $N$ 个专家计算出的 $K$ 个最高亲和度分数的集合
$mathbf{e}_{i}^{l}$ 是第 $l$ 层中第 $i$ 个专家的质心

注意 $g_{i, t}$ 是稀疏的，这表明只有 $K$ 个门值在 $N$ 个中是非零的。这种稀疏性确保了 MoE 层内的计算效率，即每个 token 只会被分配到并计算在 $K$ 个专家中

3.2.3细粒度专家分割

具体来说

在下图a所示的典型MoE架构的基础上，通过将FFN中间隐藏维度减少到 $rac{1}{m}$ 其原始大小(比如下图m=2)，从而将每个专家FFN分割成 $m$ 个更小的专家
由于每个专家变得更小，特此可以增加激活专家的数量到??倍，以保持相同的计算成本，如下图b所示(正因为m=2，所以下图b有2N个专家)

通过细粒度的专家分割，MoE层的输出可以表示为

$h_t^l = sum_{i=1}^{mN} (g_{i,t} ext{FFN}_i (u_t^l) + u_t^l)$

$g_{i,t} = egin{cases} s_{i,t} & ext{if } s_{i,t} in ext{Top}_k({s_{j,t} | 1 leq j leq mN}, mK) \ 0 & ext{otherwise} end{cases}$

$s_{i,t} = ext{Softmax}_i (u_t^{lT} e_i)$

$mathbf{u}_{1: T}^{l} in mathbb{R}^{T imes d}$ 表示第 $l$ 层注意力模块的所有token的隐藏状态

$mathbf{h}_{t}^{l} in mathbb{R}^{d}$ 是第 $l$ 层transformer块后第 $t$ 个token的输出隐藏状态

其中专家参数的总数等于 $N$ 乘以标准FFN中的参数数量，并且 $mN$ 表示细粒度专家的总数。通
过细粒度专家分割策略，非零门的数量也将增加到 $mK$ (相当于K从2到了4)

举个例子，如果?? =16，一个典型的top-2路由策略可以产生 $inom{16}{2}=120$ 种可能的组合。相比之下，如果每个专家被分成4个更小的专家，细粒度路由策略可以产生 $inom{64}{8}=4,426,165,368$ 种
潜在的组合，组合灵活性的激增增强了实现更准确和有针对性的知识获取的潜力

3.2.4共享专家隔离

在传统的路由策略中，分配给不同专家的token可能需要一些共同的知识或信息。因此，多个专家可能会在各自的参数中获取共享知识，从而导致专家参数的冗余

然而，如果有共享专家专门用于捕捉和整合不同上下文中的共同知识，那么其他路由专家之间的参数冗余将会减少
这种冗余的减少将有助于构建一个参数更高效且专家更专业化的模型
为实现这一目标，除了细粒度的专家分割策略外，DeepSeekMoE进一步隔离了 $K_{s}$ 个专家作为共享专家，使得无论路由模块如何，每个token都将被确定性地分配给这些共享专家

为了保持恒定的计算成本，其他路由专家中被激活的专家数量将减少 $K_{s}$ ，如下图c所示

在集成了共享专家隔离策略后，完整的 DeepSeekMoE 架构中的 MoE 层公式如下

$egin{array}{l} mathbf{h}_{t}{l}=sum_{i=1}{K_{s}} operatorname{FFN}_{i}left(mathbf{u}_{t}^{l} ight)+sum_{i=K_{s}+1}^{m N}left(g_{i, t} operatorname{FFN}_{i}left(mathbf{u}_{t}^{l} ight) ight)+mathbf{u}_{t}^{l}, \ g_{i, t}=left{egin{array}{ll} s_{i, t}, & s_{i, t} in operatorname{Topk}left(left{s_{j, t} mid K_{s}+1 leqslant j leqslant m N ight}, m K-K_{s} ight), \ 0, & ext { otherwise, } end{array} ight. \ s_{i, t}=operatorname{Softmax}_{i}left(mathbf{u}_{t}{l{T}} mathbf{e}_{i}^{l} ight) . end{array}$

最后，在 DeepSeekMoE 的完整结构中

共享专家的数量是 $K_{s}$ ，相当于1
路由专家的总数是 $m N-K_{s}$ ，相当于2N-1
非零门的数量是 $m K-K_{s}$ (如果没有共享专家则是mK，有共享专家则减掉共享专家即可)，相当于4 - 1 = 3

3.2.5负载平衡：专家级平衡损失、设备级平衡损失

自动学习的路由策略可能会遇到负载不平衡的问题，这会表现出两个显著缺陷

首先，存在路由崩溃的风险(Shazeer等人，2017年)，即模型总是选择少数几个专家，导致其他专家无法得到充分训练
其次，如果专家分布在多个设备上，负载不平衡会加剧计算瓶颈

为了减轻路由崩溃的风险，他们采取了以下两种措施

第一种，专家级平衡损失

其中 ??1是一个称为专家级平衡因子的超参数，路由专家的数量 $N^{prime}$ 等于 $m N-K_{s}$ ，非零门的数量 $K^{prime}$ 等于 $m K-K_{s}$ ，表示indicator function

我个人觉得上面这种表述其实挺难理解的，其实通俗点来说，可以如下理解

可以限制每个专家处理的token数量——相当于专家容量，当一个专家的容量达到上限时(比如下图中每个专家的容量是3，这个3 算是代表容量因子)，剩余的token自动会发送给下一个专家

如果被选中的两个专家的容量都已满，则token将不会被任何专家处理，而是被发送给下一层——相当于token溢出(下图图源)

此外，为方便大家的理解，我解释一下上面提到的容量因子的概念

容量因子，简言之，其决定了每个专家可以处理多少个token

其组成部分也很直接

如果增加容量因子，每个专家就能处理更多的 token——当然了，如果容量因子过大会浪费计算资源；相反，如果容量因子过小，由于 token 溢出，模型性能将下降

第二种，设备级平衡损失

当旨在缓解计算瓶颈时，在专家级别强制执行严格的平衡约束变得不必要，因为对负载平衡的过度约束会损害模型性能

相反，主要目标是确保设备间的计算平衡。如果将所有路由的专家划分为组 $left{mathcal{E}_{1}, mathcal{E}_{2}, ldots, mathcal{E}_{D} ight}$ ，并将每组部署在一个设备上，则设备级平衡损失计算如下

$egin{aligned} mathcal{L}_{ ext {DevBal }} & =alpha_{2} sum_{i=1}^{D} f_{i}^{prime} P_{i}^{prime} \ f_{i}^{prime} & =rac{1}{left|mathcal{E}_{i} ight|} sum_{j in mathcal{E}_{i}} f_{j} \ P_{i}^{prime} & =sum_{j in mathcal{E}_{i}} P_{j} end{aligned}$

其中 ??2是一个称为设备级平衡因子的超参数

在实践中，一般设置一个较小的专家级平衡因子以减轻路由崩溃的风险，同时设置一个较大的设备级平衡因子以促进设备之间的计算平衡

// 待更

第四部分DeepSeekMoE对MoE架构的实现

// 待更

前言

第一部分首个开源MoE大模型Mixtral 8x7B

1.1 Mixtral 8x7B的整体架构与模型细节

1.1.1 Mixtral 8x7B是一个稀疏的专家混合网络(即Sparse MoE)

1.1.2Mixtral的参数总量为何是46.7B而非56B

1.1.3Mixtral中所采取的GQA机制

1.1.4Mixtral中的路由(Gating/Router)

1.2 模型表现：匹配或超越Llama 2 70B 以及 GPT3.5

1.3 指令遵循模型Mixtral 8x7B Instruct

第二部分Mixtral(MOE架构)的实现细节：代码解读

2.1 MOE模块的前向传播：整体流程

2.1.1获取各token对应的top2 expert及其权重

2.1.2将各token传入对应的expert模型中进行前向传播得到输出

3.2 MOE前向传播中五个代码块的细致分析：鞭辟入里

3.2.1代码块A：routing_weights的具体样例

3.2.2 代码块B：expert_mask[expert_idx]

3.2.3 代码块C：idx, top_x = torch.where(expert_mask[expert_idx])

3.2.4 代码块D：expert内部的前向传播

3.2.5 代码块E：final_hidden_states

第三部分 DeepSeekMoE的创新：细粒度专家分割与共享专家隔离(含DeepSeek LLM的详解)

3.1DeepSeek LLM(7B、67B)的预训练与对齐

3.1.1 架构设计、预训练、并行训练等细节

3.1.2 对齐：监督微调与DPO

3.2DeepSeekMoE(16B)的创新：细粒度专家分割与共享专家隔离

3.2.1 为何提出细粒度专家分割和共享专家隔离

3.2.2 前情回顾：基于transformer的传统MoE结构

3.2.3细粒度专家分割

3.2.4共享专家隔离

3.2.5负载平衡：专家级平衡损失、设备级平衡损失

第四部分DeepSeekMoE对MoE架构的实现

猜你喜欢

目录

热门文章