---

前言

前面已经介绍过如何在数字系统中如何进行傅里叶变换，总的来说是对于一个离散无限长的序列进行截断的DTFT再进行频域采样获得DFT，或者是对于DFS取其中一个周期，然后再进行时间抽取或者频率抽取方式最终得到了FFT。

本章内容是对于无限长非周期序列进行DFT的过程中，如何进行截断，以及时域截断带来的频谱泄露是如何产生的，同时对于DTFT频域采样会有什么影响，并且如何解决频谱泄露做一个深入介绍。

|版本声明：山河君，未经博主允许，禁止转载

---

一、时域截断

1.定义

我们知道在数字系统中，处理的是有限时长信号，而不能处理无限时长信号。为了能够进行频谱分析，在音频进阶学习二十——DFT离散傅里叶变换文章中说过，我们通过对于序列的截断，再进行周期延拓形成了DFS，取其中一个周期分析形成了DFT。

而在这个过程中，需要在某个时间窗口内截取信号数据，而这个截取操作等价于将信号乘以一个矩形窗函数，也就是时域截断.

2.矩形窗口

在实际对于信号进行傅里叶变换时，我们只能处理一段有限长度的信号，因此需要进行截断。当我们截取信号长度为$L$的序列，实际上是对于信号乘上了一个长度$L$的矩形窗，数学表示如下：
$$x_{trunc}[n]=x[n]\times w_{rect}[n],w_{rect}[n]=\{\begin{array}{l}1,0\le n\le L-1\\ 0,otherwise\end{array}$$
其中$w_{rect}[n]$就是一个矩形窗，此时仅在$[0,L]$时间段内保留信号，而在其他时间点上信号被认为是零。

3.时间截断带来的影响

在音频进阶学习十——DTFT的条件、性质与举例中，介绍过对于傅里叶变换，时域点乘等于频域卷积，结合上文中矩形窗口即：
$$x[n]\times w_{rect}[n]\stackrel{DTFT}{⟷}X(e^{j\omega })\ast W(e^{j\omega })$$
也就是说，在时域上进行截断，相当于在频域上用矩形窗的频谱进行卷积。那么此时就需要考虑矩形窗频谱带来的影响。

4.窗口频谱分析

1）窗口的DTFT

现在求$w_{rect}[n]$的DTFT，在$[0,L]$区间$w_{rect}[n]=1$，如下：
$$W(e^{j\omega })=\sum _{n=0}^{L-1}{w}_{rect}[n]e^{-j\omega n}=\sum _{n=0}^{L-1}{e}^{-j\omega n}$$
这个求和是一个有限项的几何级数，其求和公式为：
$$\sum _{n=0}^{L-1}{r}^n=\frac{1-r^L}{1-r},r=e^{-j\omega }$$
即$w_{rect}[n]$的DTFT为
$$W(e^{j\omega })=\frac{1-e^{-j\omega L}}{1-e^{-j\omega }}$$
对其进行变形：
$$\begin{gathered} W(e^{j\omega })=\frac{1-e^{-j\omega L}}{1-e^{-j\omega }} \\ =\frac{e^{\frac{-j\omega L}{2}}\times (e^{\frac{j\omega L}{2}}-e^{\frac{-j\omega L}{2}})}{e^{\frac{-j\omega }{2}}\times (e^{\frac{j\omega }{2}}-e^{\frac{-j\omega }{2}})} \\ =\left(\frac{e^{\frac{-j\omega L}{2}}}{e^{\frac{j\omega }{2}}}\right)\times \left(\frac{e^{\frac{j\omega L}{2}}-e^{\frac{-j\omega L}{2}}}{e^{\frac{j\omega }{2}}-e^{\frac{-j\omega }{2}}}\right) \end{gathered}$$
根据欧拉公式$e^{j\theta }-e^{-j\theta }=2j\sin \theta$，所以上式最终为：
$$W(e^{j\omega })=e^{-j\frac{L-1}{2}\omega }\times \frac{\sin (\frac{L\omega }{2})}{\sin (\frac{\omega }{2})}$$
其中对于$e^{-j\frac{L-1}{2}}$的幅度一直是1，即这一部分只改变了相位。

2）sinc函数

sinc函数是一个非常重要的数学函数，尤其在信号处理、傅里叶分析以及采样定理中有着广泛的应用。它的标准形式是：
$$sinc=\frac{sin(\pi x)}{\pi x}$$
使用工具画出来看起来如下：

而对于
$$W(e^{j\omega })=e^{-j\frac{L-1}{2}\omega }\times \frac{\sin (\frac{L\omega }{2})}{\sin (\frac{\omega }{2})}$$
中的$\frac{\sin (\frac{L\omega }{2})}{\sin (\frac{\omega }{2})}$部分，正是 sinc 函数 的离散形式。

3）主瓣与旁瓣

主瓣和旁瓣的含义如下：

• 主瓣是频谱中最重要的部分，通常包含了大部分的能量。它的位置在sinc函数或其他频谱形状的主峰，并且在频率轴上占据最宽的区域。
• 旁瓣是主瓣两侧的峰值。它们描述了主瓣以外的部分，通常代表频谱中的其他成分。它的位置在主瓣两侧，sinc 函数的值逐渐减小并交替出现正负旁瓣。旁瓣的幅度会快速衰减，但永远不会完全为零。

对于上式$W(e^{j\omega })$找到它的主瓣，就要找到主瓣的零点，也就是$sin(\frac{L\omega }{2})=0$的时候，也就是
$$\frac{L\omega }{2}=\pi ,\omega =\pm \frac{2\pi }{L}$$
这意味着，主瓣的宽度大约是从$-\frac{2\pi }{L}$到$\frac{2\pi }{L}$，也就是说主瓣的宽度与$L$的大小成反比，如同下图：

5.频域卷积结果

上文中说过，在时域上进行截断，相当于在频域上用矩形窗的频谱进行卷积。现在举一个例子看一下卷积的结果。

假设：

• 序列$x[n]$由两个余弦信号组成：$x[n]=A_0\cos ({\omega }_{0}n)+A_1\cos ({\omega }_{1}n)$
• 序列$x[n]$的DTFT为：$X(e^{j\omega })=A_0\delta (\omega +{\omega }_0)+A_0\delta (\omega -{\omega }_0)+A_1\delta (\omega +{\omega }_1)+A_1\delta (\omega -{\omega }_1)$
  即在频域上关于零点对称，即由四根谱线组成（权重归一化）
• 窗函数的频谱由上文可知：$W(e^{j\omega })=e^{-j\frac{L-1}{2}\omega }\times \frac{\sin (\frac{L\omega }{2})}{\sin (\frac{\omega }{2})}$
• 两者卷积为（由音频进阶学习十——DTFT的条件、性质与举例可知）：$V(e^{j\omega })=X(e^{j\omega })\ast W(e^{j\omega })=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\theta })W(e^{j(\omega -\theta )})d\theta$

此时对于$V(e^{j\omega })$展开计算：
$$\begin{gathered} V(e^{j\omega })=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\theta })W(e^{j(\omega -\theta )})d\theta \\ =\frac{1}{2\pi }{\int }_{-\pi }^{\pi }(A_0\delta (\omega +{\omega }_0)+A_0\delta (\omega -{\omega }_0)+A_1\delta (\omega +{\omega }_1)+A_1\delta (\omega -{\omega }_1))(W(e^{j(\omega -\theta )})d\theta \end{gathered}$$
根据积分的线性和冲激函数的性质有：
$${\int }_{-\infty }^{\infty }f(x)\delta (x-a)dx=f(a)$$
上式则最终为（权重归一化）：
$$V(e^{j\omega })=\frac{A_0}{2}W(e^{j(\omega +{\omega }_0)})+\frac{A_0}{2}W(e^{j(\omega -{\omega }_0)})+\frac{A_1}{2}W(e^{j(\omega +{\omega }_1)})+\frac{A_1}{2}W(e^{j(\omega -{\omega }_1)})$$
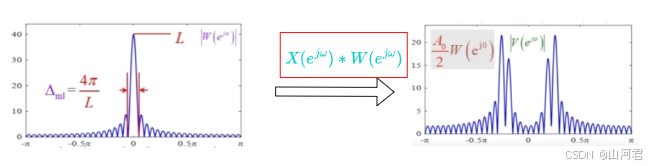
查看最终结果，也就是在这个例子中，对于$V(e^{j\omega })$相当于将$W(e^{j\omega })$分别移位到$\pm {\omega }_0$和$\pm {\omega }_1$上，并进行幅度缩小处理再叠加，如下图：

二、时域加窗

1.加窗带来的影响

上文中的序列为$x[n]$由两个余弦信号组成：$x[n]=A_0\cos ({\omega }_{0}n)+A_1\cos ({\omega }_{1}n)$。对于序列的截断，同时造成了频域上用矩形窗的频谱进行卷积。此时得到最终的频域就会受到主瓣和旁瓣的影响。

1）主瓣带来的影响

对于序列$x[n]$来说，它的频谱是四根谱线组成，也就是说在频域上的表示每一个谱线是无限窄的。但是在进行截断加窗以后，每根谱线就变成了有宽度的，宽度大约是从$-\frac{2\pi }{L}$到$\frac{2\pi }{L}$，如同下图：

而主瓣的宽度是和$L$成反比，也就是说$L$越大，宽度越窄，$L$越小，宽度越大，这就会带来展宽的影响，如同下图中，当序列$x[n]$的四根谱线越来越接近的时候，由于受到矩形窗主瓣的影响，四根谱线逐渐就分不清楚了。

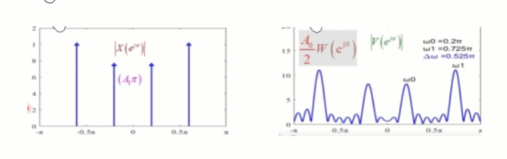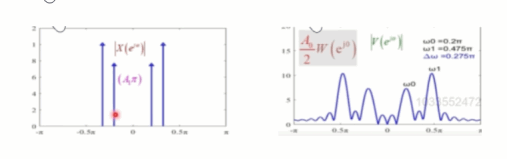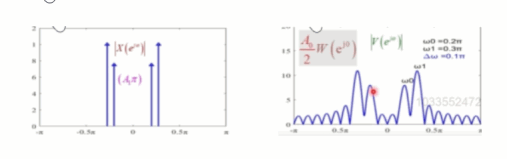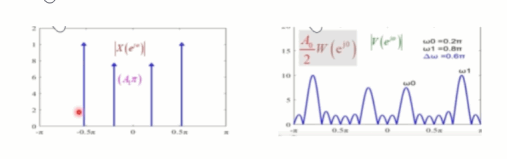
为了避免这种影响，就需要减少主瓣的宽度，也就是增加$L$的取值，如同下图：

2）旁瓣的影响

• 发生了频谱泄露：如同下图，很明显的经过频域卷积后，新引入了不同的频率分量。
  
• 随着序列幅度的减小，卷积后的信号显然无法再区分序列本身的幅度了。
  

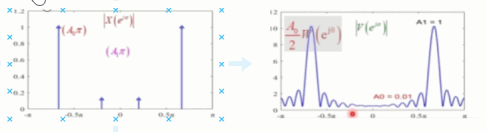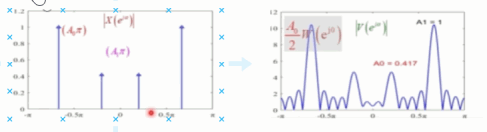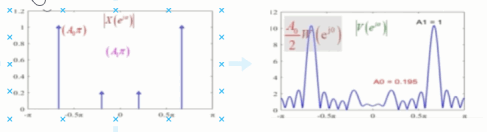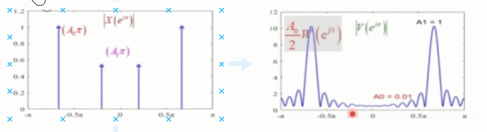
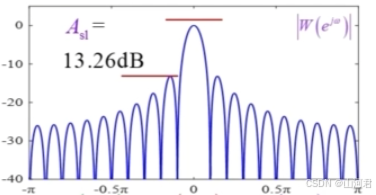
我们将信号幅度转为db（幅度比而非功率比）有第一旁瓣和主瓣的比值为：$20{\log }_{10}(\frac{|W(e^{j{\omega }_1})|}{|W(e^{j0})|})=20{\log }_{10}(0.217)=-13.26db$。如同下图：

而当序列$A_0=1,A_1=0.01,{\omega }_0=\frac{2\pi }{3},{\omega }_1=\pi 5$时，$20{\log }_{10}(\frac{A_1}{A_0})=-40db$，已经再旁瓣的里面了。

为了消除这种影响，就需要降低旁瓣的高度。

2.汉宁窗

为了解决上文中主瓣和旁瓣带来的影响，我们需要：

• 主瓣影响：增加$L$的值
• 旁瓣影响：减少旁瓣的高度

此时，引用了另外的窗口来替换矩形窗口，这里举一个汉宁窗的例子：
$$Hanning:w[n]=0.5-0.5\cos (\frac{2\pi n}{L-1}),0\le n\le L-1$$

1）汉宁窗的DTFT

它的DTFT可以通过如下方式求得,已知余弦函数的欧拉公式为：
$$\cos (x)=\frac{e^{jx}+e^{-jx}}{2}$$
即$w[n]$为：
$$w[n]=0.5-0.5\cos (\frac{2\pi n}{L-1})=0.5-0.25e^{j\frac{w\pi n}{L-1}}-0.25e^{-j\frac{w\pi n}{L-1}}$$
即它的DTFT为：
$$\begin{gathered} W(e^{j\omega })=\sum _{n=0}^{L-1}(0.5-0.25e^{j\frac{w\pi n}{L-1}}-0.25e^{-j\frac{w\pi n}{L-1}})e^{-j\omega n} \\ =0.5\sum _{n=0}^{L-1}{e}^{-j\omega n}-0.25\sum _{n=0}^{L-1}{e}^{-j(\omega -\frac{w\pi n}{L-1})n}-0.25\sum _{n=0}^{L-1}{e}^{-j(\omega +\frac{w\pi n}{L-1})n} \end{gathered}$$
根据一个有限项的几何级数，其求和为：
$$W(e^{j\omega })=0.5\frac{1-e^{-j\omega L}}{1-e^{-j\omega }}-0.25\frac{1-e^{-jL(\omega -\frac{2\pi }{L-1})}}{1-e^{-j(\omega -\frac{2\pi }{L-1})}}-0.25\frac{1-e^{-jL(\omega +\frac{2\pi }{L-1})}}{1-e^{-j(\omega +\frac{2\pi }{L-1})}}$$
再将其转成sinc函数的形式，最终得到：
$$W(e^{j\omega })\approx \frac{1}{2}Lsinc(\frac{L\omega }{2\pi })-\frac{1}{4}Lsinc(\frac{L(\omega -\frac{2\pi }{L-1}))}{2\pi })--\frac{1}{4}Lsinc(\frac{L(\omega +\frac{2\pi }{L-1}))}{2\pi })$$

2）矩形窗和汉宁窗的幅度比

我们使用matlab画出来矩形窗和汉宁窗的幅度比

% 窗口长度
L = 64;

% 创建矩形窗和汉宁窗
rect_win = ones(1, L);                  % 矩形窗
hanning_win = hanning(L);               % 汉宁窗

% 计算频谱（FFT）
rect_fft = abs(fftshift(fft(rect_win, 1024)));    % 计算矩形窗的频谱
hanning_fft = abs(fftshift(fft(hanning_win, 1024)));  % 计算汉宁窗的频谱

% 频率轴
f = (-512:511)/512;   % 归一化频率轴

% 转换为 dB（归一化到最大值）
rect_dB = 20*log10(rect_fft / max(rect_fft));
hanning_dB = 20*log10(hanning_fft / max(hanning_fft));

% 绘图
figure;

% 矩形窗频谱
subplot(2, 1, 1);
plot(f, rect_dB, 'b', 'LineWidth', 2);
title('矩形窗频谱');
xlabel('Normalized Frequency (cycles/sample)');
ylabel('Magnitude (dB)');
grid on;
xlim([-0.5, 0.5]);
ylim([-50, 0]);

% 汉宁窗频谱
subplot(2, 1, 2);
plot(f, hanning_dB, 'r', 'LineWidth', 2);
title('汉宁窗频谱');
xlabel('Normalized Frequency (cycles/sample)');
ylabel('Magnitude (dB)');
grid on;
xlim([-0.5, 0.5]);
ylim([-50, 0]);

% 调整图形
sgtitle('矩形窗与汉宁窗频谱比较');

得到的图像画出来如下，可以很明显的看到：

窗函数	第一旁瓣幅度 (dB)	旁瓣下降速度
矩形窗	-13.3 dB	约 -6 dB/倍频
汉宁窗	-31.5 dB	约 -18 dB/倍频

这意味着：

• 矩形窗的频谱旁瓣较高（-13.3 dB），这意味着窗口截断后的信号会产生较多的频谱泄露。汉宁窗降低了旁瓣（-31.5 dB），使得远离主频率的能量衰减更快，减少了旁瓣带来的干扰。
• 矩形窗的主瓣较窄，但由于窗口是突然截断的，会产生高旁瓣。汉宁窗通过平滑过渡（两端收敛到 0），让主瓣更平滑，减少频谱振荡。
  

3.常用窗口

窗口类型	时域表达式	主瓣宽度 (Δf, 归一化频率)	第一旁瓣衰减 (dB)	旁瓣衰减速率 (dB/倍频)	特点
矩形窗	$w[n]=1$	$\frac{4\pi }{L}$	-13.3 dB	-6 dB/倍频	最窄主瓣，最大频谱泄露，旁瓣较高
汉宁窗	$w[n]=0.5-0.5\cos \left(\frac{2\pi n}{L-1}\right)$	$\frac{8\pi }{L}$	-31.5 dB	-18 dB/倍频	旁瓣低，频谱泄露小，适用于频谱分析
汉明窗	$w[n]=0.54-0.46\cos \left(\frac{2\pi n}{L-1}\right)$	$\frac{8\pi }{L}$	-42.7 dB	-6 dB/倍频	旁瓣比汉宁窗低但主瓣相似，适用于滤波
布莱克曼窗	$w[n]=0.42-0.5\cos \left(\frac{2\pi n}{L-1}\right)+0.08\cos \left(\frac{4\pi n}{L-1}\right)$	$\frac{12\pi }{L}$	-58.1 dB	-18 dB/倍频	旁瓣极低，但主瓣更宽
凯泽窗 (β=5)	$w[n]=I_0\left(\beta \sqrt{1-(\frac{2n}{L-1}-1{)}^2}\right)$	取决于 β	取决于 β	取决于 β	可调参数 β，适用于自定义性能需求

• 矩形窗：主瓣最窄，但旁瓣高，适用于时间截断，但频谱泄露严重。
• 汉宁窗：较低旁瓣，适用于频谱分析。
• 汉明窗：比汉宁窗稍好，常用于 FIR 滤波器设计。
• 布莱克曼窗：较宽主瓣，但旁瓣极低，适用于高精度分析。
• 凯泽窗：可调 β 值，适用于灵活的窗口设计。

三、栅栏效应

上文对于信号的截断相当于加窗，而加窗后我们还需要得到DFT，也就是：
$$v[n]=x[n]\times w[n],V(e^{j\omega })=X(e^{j\omega })\ast W(e^{j\omega }),V[k]=V(e^{j\omega }){|}_{\omega =\frac{2\pi }{N}}$$

1.定义

栅栏效应是由于离散傅里叶变换（DFT/FFT）的频域离散化特性导致的，它是指频谱只能在离散的频率点上被观测到。当频率分量$k=0,1,\mathrm{2...},N-1$,如果信号的真实频率不在这些离散点上，其能量会“泄漏”到邻近的频率点，导致频谱分析出现误差。

使用matlab画出正弦波频率分量为32，64，128，和256时的频谱

clc; clear; close all;

% 设置信号参数
fs = 100;          % 采样频率 (Hz)
f_sig = 12.3;      % 信号频率 (Hz)，故意设成非整数，以产生栅栏效应
T = 1/fs;          % 采样周期

% 设置不同的 FFT 点数
N_values = [32, 64, 128, 256];  % 不同的 FFT 点数
colors = ['r', 'g', 'b', 'k'];  % 颜色标识
figure;

for i = 1:length(N_values)
    N = N_values(i);   % 当前 FFT 点数
    t = (0:N-1) * T;   % 时间向量
    x = sin(2*pi*f_sig*t);  % 生成正弦信号
    
    % 计算 FFT
    X = abs(fft(x, N)); 
    X = X / max(X); % 归一化

    % 计算频率轴
    f = (0:N-1) * (fs/N);  % 频率轴
    
    % 仅绘制前半部分（FFT 对称）
    subplot(2,2,i);
    plot(f(1:N/2), X(1:N/2), colors(i), 'LineWidth', 1.5);
    title(['N = ', num2str(N)]);
    xlabel('频率 (Hz)');
    ylabel('归一化幅度');
    grid on;
end

sgtitle('栅栏效应随 N 变化的影响');

2.如何缓解

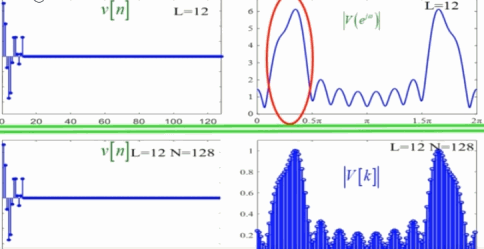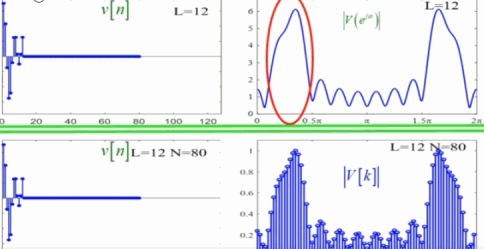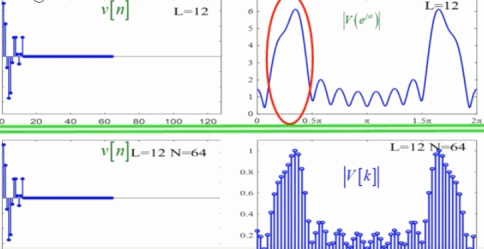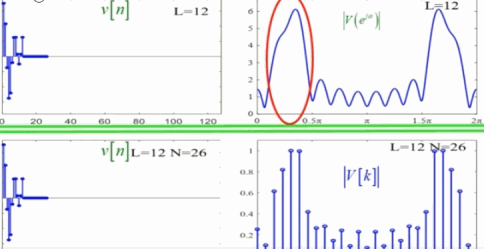
此时如果截断长度$L$不变，而频域采样$N$发生变化，经过加窗后，随着N的增大，栅栏效应变小，如同下图：

---

总结

本篇文章着重介绍了时域截断的影响，时域截断等于时域加窗，序列频域和窗口频域进行卷积。此时会造成频谱泄露，通过不同的窗口函数我们可以减少这种频谱泄露。同时，对于加窗和频域采样的长度影响做了介绍。这对于后面设计滤波器考虑平滑输出有着重大作用。

那么下一篇文章中，将真正开始介绍如何设计一个滤波器。

反正收藏也不会看，不如点个赞吧！