什么是卡方检验
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
它在分类资料统计推断中的应用,包括:两个率或两个构成比比较的卡方检验;多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。
例子1:四格卡方检验
以下为一个典型的四格卡方检验,我们想知道喝牛奶对感冒发病率有没有影响:
| 感冒人数 | 未感冒人数 | 合计 | 感冒率 | |
| 喝牛奶组 | 43 | 96 | 139 | 30.94% |
| 不喝牛奶组 | 28 | 84 | 112 | 25.00% |
| 合计 | 71 | 180 | 251 | 28.29% |
通过简单的统计我们得出喝牛奶组和不喝牛奶组的感冒率为30.94%和25.00%,两者的差别可能是抽样误差导致,也有可能是牛奶对感冒率真的有影响。
为了确定真实原因,我们先假设喝牛奶对感冒发病率是没有影响的,即喝牛奶喝感冒时独立无关的,所以我们可以得出感冒的发病率实际是(43+28)/(43+28+96+84)= 28.29%
所以,理论的四格表应该如下表所示:
| 感冒人数 | 未感冒人数 | 合计 | |
| 喝牛奶组 | =139*0.2829 | =139*(1-0.2829) | 139 |
| 不喝牛奶组 | =112*0.2829 | =112*(1-0.2829) | 112 |
即下表:
| 感冒人数 | 未感冒人数 | 合计 | |
| 喝牛奶组 | 39.3231 | 99.6769 | 139 |
| 不喝牛奶组 | 31.6848 | 80.3152 | 112 |
| 合计 | 71 | 180 | 251 |
如果喝牛奶喝感冒真的是独立无关的,那么四格表里的理论值和实际值差别应该会很小。
卡方检验
卡方检验的计算公式为:

其中,A为实际值,T为理论值。
x2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
1. 实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的)
2. 差异程度与理论值的相对大小
例1卡方检验
根据卡方检验公式我们可以得出例1的卡方值为:
卡方 = (43 - 39.3231)平方 / 39.3231 + (28 - 31.6848)平方 / 31.6848 + (96 - 99.6769)平方 / 99.6769 + (84 - 80.3152)平方 / 80.3152 = 1.077
卡方分布的临界值:
上一步我们得到了卡方的值,但是如何通过卡方的值来判断喝牛奶和感冒是否真的是独立无关的?也就是说,怎么知道无关性假设是否可靠?
答案是,通过查询卡方分布的临界值表。
这里需要用到一个自由度的概念,自由度等于V = (行数 - 1) * (列数 - 1),对四格表,自由度V = 1。
对V = 1,喝牛奶和感冒95%概率不相关的卡方分布的临界概率是:3.84。即如果卡方大于3.84,则认为喝牛奶和感冒有95%的概率不相关。
显然1.077<3.84,没有达到卡方分布的临界值,所以喝牛奶和感冒独立不相关的假设不成立。

上面通过一个小例子让大家对卡方检验有一个简单的认识,下面是卡方检验的标准做法:
例子2. 四格卡方检验的标准做法
我们想知道不吃晚饭对体重下降有没有影响:
| 体重下降 | 体重未下降 | 合计 | 体重下降率 | |
| 吃晚饭组 | 123 | 467 | 590 | 20.85% |
| 不吃晚饭组 | 45 | 106 | 151 | 29.80% |
| 合计 | 168 | 573 | 741 | 22.67% |
1. 建立假设检验:
H0:r1=r2,不吃晚饭对体重下降没有影响,即吃不吃晚饭的体重下降率相等;
H1:r1≠r2,不吃晚饭对体重下降有显著影响,即吃不吃晚饭的体重下降率不相等。α=0.05
2. 计算理论值
| 体重下降 | 体重未下降 | 合计 | |
| 吃晚饭组 | 133.765 | 456.234 | 590 |
| 不吃晚饭组 | 34.2348 | 116.765 | 151 |
| 合计 | 168 | 573 | 741 |
3. 计算卡方值
根据公式

计算出卡方值为5.498
4. 查卡方表求P值
在查表之前应知本题自由度。按卡方检验的自由度v=(行数-1)(列数-1),则该题的自由度v=(2-1)(2-1)=1,查卡方界值表,找到3.84,而本题卡方=5.498即卡方>3.84,P<0.05,差异有显著统计学意义,按α=0.05水准,拒绝H0,可以认为两组的体重下降率有明显差别。
通过实例计算,对卡方的基本公式有如下理解:若各理论数与相应实际数相差越小,卡方值越小;如两者相同,则卡方值必为零。
附录
什么是卡方分布
若n个相互独立的随机变量ξ₁,ξ₂,...,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
R语言实现:
-
x1 = rnorm( 1000000)
-
x2 = rnorm( 1000000)
-
x3 = rnorm( 1000000)
-
x4 = rnorm( 1000000)
-
x5 = rnorm( 1000000)
-
x6 = rnorm( 1000000)
-
-
Q1 = x1^ 2
-
Q2 = x1^ 2 + x2^ 2
-
Q3 = x1^ 2 + x2^ 2 + x3^ 2
-
Q4 = x1^ 2 + x2^ 2 + x3^ 2 + x4^ 2
-
Q5 = x1^ 2 + x2^ 2 + x3^ 2 + x4^ 2 + x5^ 2
-
Q6 = x1^ 2 + x2^ 2 + x3^ 2 + x4^ 2 + x5^ 2 + x6^ 2
-
-
par(mfrow=c( 1, 1))
-
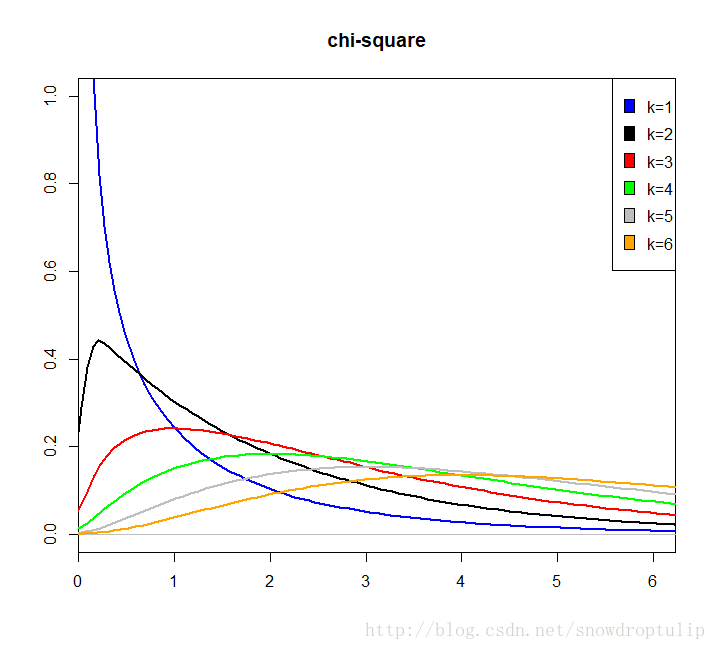
plot(density(Q1),xlim=c( 0.23, 6),ylim = c( 0, 1),breaks = 200,col = 'blue',lwd= 2,main= 'chi-square',xlab = '',ylab= '')
-
lines(density(Q2),col= 'black',lwd= 2)
-
lines(density(Q3),col= 'red',lwd= 2)
-
lines(density(Q4),col= 'green',lwd= 2)
-
lines(density(Q5),col= 'gray',lwd= 2)
-
lines(density(Q6),col= 'orange',lwd= 2)
-
legend( 'topright',c( 'k=1', 'k=2', 'k=3', 'k=4', 'k=5', 'k=6'),fill = c( 'blue', 'black', 'red', 'green', 'gray', 'orange'))
最后画出来的图是:
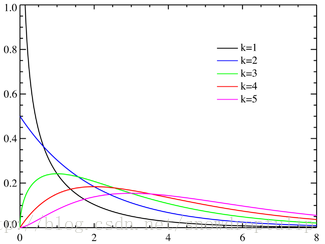
由于随机数取得比较少,可能分布图与实际有些许的差别,不过这个可以不用太在意,一下是标准的分布图:
转自:https://blog.csdn.net/snowdroptulip/article/details/78770088