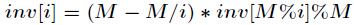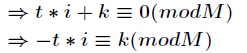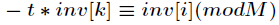1.费马小定理求逆元(求a对于mod的逆元,要求mod为素数)
由费马小定理 a^(p-1)≡1 , 变形得 a*a^(p-2)≡1(mod p),答案已经很明显了:若a,p互质,因为a*a^(p-2)≡1(mod p)且a*x≡1(mod p),则x=a^(p-2)(mod p),用快速幂可快速求之
- 复杂度O(logn);
- 适用范围:一般在mod是个素数的时候用,比扩欧快一点而且好写。
ll power_mod(ll a, ll b, ll mod)
{
ll ans = 1;
while (b)
{
if (b & 1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
inv2 = power_mod(a, mod - 2, mod);
2.扩展欧几里得
给定模数m,求a的逆相当于求解ax=1(mod m)
这个方程可以转化为ax-my=1
然后套用求二元一次方程的方法,用扩展欧几里得算法求得一组x0,y0和gcd
检查gcd是否为1
gcd不为1则说明逆元不存在
若为1(a与m互质),则调整x0到0~m-1的范围中即可
- PS:这种算法效率较高,常数较小,时间复杂度为O(ln n)
- 适用范围:只要存在逆元即可求,适用于个数不多但是mod很大的时候,也是最常见的一种求逆元的方法。
typedef long long ll;
void extgcd(ll a,ll b,ll& d,ll& x,ll& y)
{
if(!b)
{ d=a; x=1; y=0;}
else
{
extgcd(b,a%b,d,y,x);
y-=x*(a/b);
}
}
ll inverse(ll a,ll n) //求a在mod下的逆元,不存在逆元返回-1
{
ll d,x,y;
extgcd(a,n,d,x,y);
return d==1?(x+n)%n:-1; //(x+n)%n 防止为负
}
3.逆元打表
有时会遇到这样一种问题,在模质数p下,求1~n逆元 n< p(这里
它的推导过程如下,设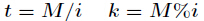
对上式两边同时除
再把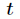
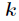
初始化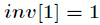

另外有个结论


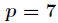
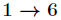
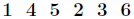
线性求逆元
typedef long long ll;
const int N = 1e5 + 5;
int inv[N];
void inverse(int n, int p)
{
inv[1] = 1;
for (int i=2; i<=n; ++i)
{
inv[i] = (ll) (p - p / i) * inv[p%i] % p;
}
}
注意:
- 调用前要先预处理
- 调用的时候要先对除数取mod
性能分析:
- 时间复杂度O(n)
- 适用范围:p是不大的素数而且多次调用,比如卢卡斯定理。
递归求逆元
LL inv(LL i)
{
if(i==1)return 1;
return (mod-mod/i)*inv(mod%i)%mod;
}性能分析
- 时间复杂度:O(logmod)
- 好像找到了最简单的算法了!!
- 适用范围: mod数是素数,所以并不好用,比如中国剩余定理中就不好使,因为很多时候可能会忘记考虑mod数是不是素数。
参考博客
https://blog.csdn.net/xiaoming_p/article/details/79644386