浅谈完备化及完备空间上的线性算子

版权声明：转载本博客原创文章，请标明出处并附上链接。 https://blog.csdn.net/fourierFeng/article/details/82974753

本文并非要涉及数学史，只追求数学上的自恰，在逻辑上能够自圆其说。

前言

数学是基于公设的，数学的进步是集合完备化与映射简洁化的共同作用 。映射的简化会催化新的定义的产生，新的定义往往又会衍生出新的完备化过程，两者此消彼长，可看成是一个过程的两个对偶的方面。
这篇文章会试着来讲述这个完备化过程，进而讲述完备化后的空间中的线性算子。简单的说完备化就是把某个函数的值域扩充进已有集合的过程。从实用的角度来看，完备化的目的是为了更好的研究线性算子（所有的对非线性算子的研究其实都是研究其如何以更加简洁的形式转化为线性）。本文首先从数的构造说起。

实数的构造

实分析用到的各种数系，按照复杂性递增的次序，它们是自然数系 $\mathbb{N}$、整数系 $\mathbb{Z}$、有理数系 $\mathbb{Q}$以及实数系 $\mathbb{Z}$。自然数系 $\left \{ 0,1,2,3,\cdots \right \}$是最原始的数系，它的一个标准定义是由皮亚诺公理给出的。从自然数到整数是对减法映射的值域做并的结果，从加法群的角度上，这是的一个完备化过程。整数加群作为核心元素，活跃在数学的所有分支。
有理数是整数对除法映射做并的结果，当然，我们必须遵从通常的禁率，分母不得为0。因为如果允许 $b$为0的话，将不能保持两个恒等式 $\left ( \frac{a}{b} \right )\times b=a$和 $c\times 0=0$同时成立，域的结构就会遭到破坏，也就失去了完备化的意义。对于有理数这个名称的由来，是翻译的rational，其实这里是数学家前辈犯的一个美丽的错误，ratio是比例的意思，nal是后缀，而不能翻译成通常的“合理的，理性的”。这样的错误以讹传讹，叫的人多了而且由于其的朗朗上口最终就索性这样传下来了。有些很个性的学者愣是在自己的著作里使用的是“比例数”而非“有理数”。
公元前500年，古希腊毕达哥拉斯学派的弟子希帕索斯发现了一个正方形的对角线与其一边的长度的比值不是有理数。这一发现使该学派领导人惶恐、恼怒，认为这颠覆了他们的信仰。希帕索斯因此遭到了沉舟身亡的惩处。
但希帕索斯的发现和思考，第一次揭示出了有理数系的缺陷，证明有理数并没有填满数轴，在数轴上还存在着大量的“孔隙”，推动数学学科向前迈进了一大步。

柯西数列构造实数

柯西数列是微积分存在的基础，它很好的定义了豪斯多夫空间的收敛的概念。为了研究微积分学，就必须构造对柯西数列完备的数系和空间，简称为数列完备。实数是柯西数列完备化有理数的结果，也可看成是柯西数列的完备集。一个有理数列可看成是一个从自然数到有理数的映射，它把每一个大于等于 $m$的序数 $n$映射到数列的一个有理数元素 $a_{n}$。当一个有理数列，对于每个有理数 $\varepsilon$，存在 $N\geqslant 0$，使得对一切 $j,k\geqslant N$，满足 $d(a_{j},a_{k})\leqslant \varepsilon$，则这个有理数列构成柯西数列。
很容易证明的是，每个柯西数列都是有界的，则所有的柯西数列的极限的集合构成实数。也可以说成柯西数列的全体构成实数域也是对的。为了保证我们的实数集合整洁（否则一个元素会出现多次），需增加限制条件，构作等价类。进一步可以证明，限制离开零（所有的元素非零）的柯西数列关于等价类构成的集合对于加、减、乘、除四个映射是封闭的。则说明构成域，即为实数域。

复数域

实数域的发现为微积分提供了完美的舞台，但实数并非最大的数域，在实数的基础上对 $i=\sqrt{-1}$完备化得到了复数域，是目前所知的最大的数域。数学家哈密顿构造了我们工程上经常用到的四元数集合，它有三个虚部，可看成是复数的扩展，但它不是域，只是个除环，比域少了交换律。
复数域的发现极大的丰富了数学的表达、计算能力，比如幂级数有着非常简单的结构和非常强大的表现力，是最简单的解析函数项级数，但在实数域是无法真正的看清楚的，直观的解释是在实数域要找一个无穷可微的函数是非常苛刻的。而在实数域可导的函数就可以很容易的扩展为复数域的解析函数，在复数域，解析函数是具有无穷可微性的，也就可以很容易的展开为幂级数，并且可进一步扩展为更为广义的洛朗级数。在幂级数理论中处于核心地位的泰勒定理是这样描述的：设 $f(z)$在区域 $D$内解析， $a\in D$，只要圆 $K$： $\left | z-a \right |<R$含于 $D$，则 $f(z)$在 $K$内能展成幂级数。而且它的逆命题也是成立的：任意一个具有非零收敛半径的幂级数在其收敛圆内收敛于一个解析函数。Z变换就是在这样的性质的基础上产生的，是针对函数离散的情况。
再比如，在实数域很难积分的情况，在复数域可能就会比较容易的得到解决，因为在复数域两点之间的有向路径很多，并不像实数域只有一条。复变函数单值解析分支上的任何积分路径都是等价的。

线性空间

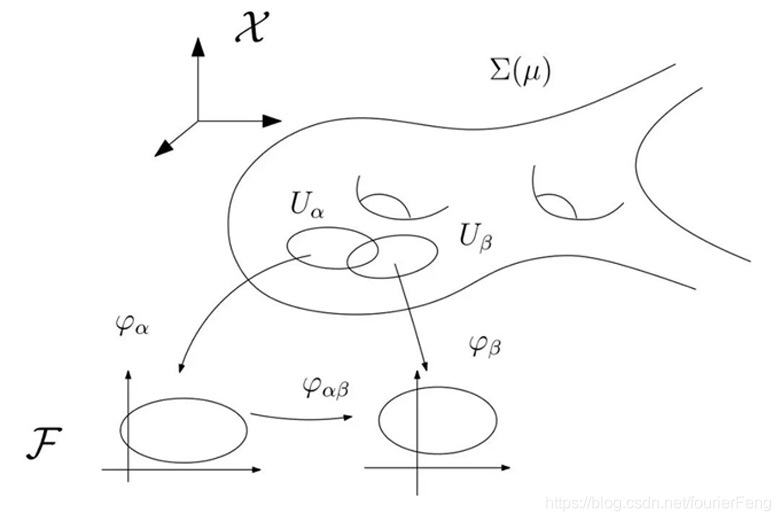
大部分的数学理论都是必须在线性空间中才能发挥作用的。一个复杂的拓扑空间，首先要想方设法的把它转化为流形，然后或者在局部构作欧式空间（见下图，图片摘自老顾谈几何），或者在流形上寻找群结构进而构作李代数，最后在构作的线性空间上进行相应的分析。线性空间也叫向量空间。

为了在线性空间中表达距离，引入了范数。为了在线性空间中同时表达角度和距离，引入了内积。引入这些映射是为了线性空间的度量，统称为度量空间。度量空间的完备化靠的也是前面讲述的柯西数列，最为常见的度量空间为欧几里得空间，傅里叶级数、黎曼积分、线性代数及欧式几何都是基于它发展起来的，在我们计算机算法中，都是在欧式空间上才能进行算法设计，数学技巧主要体现在如何把复杂的空间结构转化为欧式空间 。但对于绝大多数的计算机专业的科技人员，能掌握欧式空间的理论也已经足够了。
矩阵是一个数学模型，是对欧式空间上的线性变换的抽象，工科课程线性代数围绕着矩阵讲个不停，实际上就是在讲欧几里得空间的线性变换，这是基于如下的一个重要的定理：设 $V$和 ${V}'$分别是域 $F$上 $n$维、 $s$维线性空间，则 $V$到 ${V}'$的线性映射 $A$与它在 $V$的一个基和 ${V}'$的一个基下的矩阵 $A$的对应是线性空间 $Hom(V,{V}')$到 $M_{s\times n}(F)$的一个同构映射，从而 $Hom(V,{V}')\cong M_{s\times n}(F)$并且 $dim(Hom(V,{V}'))=s\times n=dim(V)\times dim({V}')$
在这里同构不仅仅是矩阵空间与线性映射空间的同构，它们上面的运算也是同构关系，所以可以构造矩阵范畴与线性映射范畴之间的同构态射，即是范畴之间的同构关系。在一定程度上欧几里得空间已经足够完备，所有与应用直接相关的技术问题都是基于欧几里得空间。但是，以狄拉克函数为代表的广义函数又引发了数学家的思考革命。

狄拉克函数

本世纪初，工程师Heaviside在解电路方程时，需要对如下函数求导函数 $\delta (x)$： $Y(x)=\left\{\begin{matrix} 1 & (x\geqslant 0)\\ 0& (x< 0) \end{matrix}\right.$但是在欧几里得空间上该函数并不可微，因此 $\delta (x)$不可能是函数，它除了作为一个记号，在数学上本来是没有意义的。可是，这个 $\delta (x)$在实际中却是非常重要的，它代表了一种理想化了的“瞬间”单位脉冲。所谓单位是指：积分为1。所谓瞬时，是指发生的时间区间趋于0。这在通信行业上也叫做冲激信号，描述冲激信号的就是狄拉克函数 。可在欧几里得空间中，它并不能作为一个函数去解释，这说明了欧几里得空间还不够完备，需要扩展。
学者们不久就发现了狄拉克函数的自变量是什么样的： $\delta (\varphi )=\varphi (0)\left ( \varphi \in functionSpace \right )$ 可以看到，狄拉克函数的自变量是个函数（属于基本空间 $D(\Omega )$），可否用这些函数来扩充欧几里得空间？使其完备化？这就诱导产生了希尔伯特空间。

希尔伯特空间

希尔伯特空间就是完备的内积空间，它可以是不可数维数的，也可以是可数维数的，也可以是有限维数的（欧几里得空间）。它是为了定义泛函而完备化欧几里得空间的结果。泛函，通俗的讲，它包括了传统的函数和“函数的函数”（广义函数是线性连续的，可看成是泛函的子集）。也可以简单的理解为：希尔伯特空间是把若干像狄拉克函数这样的函数包容进欧几里得空间的结果，使得得到的空间能够对狄拉克这类的函数完备。
希尔伯特空间的发现使得数学学科爆炸式增长，为了适应不同的分支，产生了很多不可数维希尔伯特空间的稠密子空间（还是希尔伯特空间），比如为了研究偏微分方程，需要刻画针对任意阶导数的收敛性，需要重新定义范数来刻画这种收敛性，这就产生了索伯列夫空间。对应于欧几里得空间中变换可逆的思想，人们发现，每个正定对称函数 $K(t,s)$都一一对应一个至多可数维的希尔伯特空间，并且非常容易的构造基底，即为再生核希尔伯特空间。这个正定对称函数 $K(t,s)$称为核函数，同时，所有的核函数也构成一个空间，通过它，复杂的希尔伯特空间得到了极大的简化。
正交变换是性质很好的一类变换，“好”首先体现在简洁，它直接对应的是正交基，可以把复杂的空间分解为若干简单的空间的直和形式。以及对乘法封闭，构成群，而且维数低；同时是个保角变换、保距变换；另外 正交变换有着非常明确的物理意义——即表示饶任意轴的旋转，当然也可以很容易的反演。标准正交基下的数学模型往往非常简单，在计算机软硬件中更容易的实现。欧几里得空间的正交矩阵的构造学过大学数学的人都应该很明白了，但接下来的问题就是希尔伯特空间的正交变换该如何构造呢？可是，不同于欧几里得空间，希尔伯特空间的基的构造并不容易，寻找既简单又正交而且“性能优越”的基底更是可遇不可求的事情。
1807年，法国数学家Fourier向法国科学院递交了一份报告，在报告中他指出，任何周期函数都可以近似表示为不同频率的正弦波和余弦波的叠加： $f(t)\approx \frac{a_{0}}{2}+\sum_{n=1}^{\infty }\left (a_{n}\mathit{cos}n\omega t+b_{n}\mathit{sin}n\omega t\right)$
更为重要的是下式的成立： $\int_{-\pi }^{\pi}cosmx\cdot cosnxdx=\int_{-\pi }^{\pi}sinmx\cdot sinnxd=\pi\delta _{m,n}$ 其中 $\delta _{m,n}=\left\{\begin{matrix} 1 & m=n\\ 0 & m\neq n \end{matrix}\right.$如上事实就表明不同频率的三角函数构成正交基。然而，该正交基是可列维的（离散的），把它扩充为不可列维（连续）空间的正交基一是为了完备化，二是为了能更加充分的而不仅仅是近似表达 $L_{2}$空间的函数。把上面的傅里叶级数形式细化为积分形式： $f(t)=\int_{0}^{\infty }\left [ u(\omega )cos\omega t+v(\omega )sin\omega t \right ]d\omega$ 这里，其实正弦函数和余弦函数是没有本质区别的，都是波函数，只不过相位不同而已，而他们的系数又是不同的函数，格式上的冗余在数学领域是不能容忍的。作为最令人着迷的公式——欧拉公式： $e^{\pi i}+1=0$，可推导得到更一般的： $e^{ix}=cos(x)+isin(x)$表明，如函数 $f$可以用指数级数线性表出，那么 $f$也可以写成实数域傅里叶级数形式。指数级数形式在很多文献中也称为复数域的傅里叶级数。设 $e_{k}(x)=e^{2\pi ikx}$，则 $\left \langle e_{k},e_{l} \right \rangle=\left\{\begin{matrix} 1, & if k=l\\ 0,& if k\neq l \end{matrix}\right.$可知周期或连续指数映射构成一个希尔伯特空间的正交基，而且形式上比实数域的三角函数还要简洁！这样函数 $f$就可表示为 $f(x)\approx\sum_{k\in \mathbb{Z}}^{ } c_{k}e^{2\pi ikx}$对每个 $k$， $c_{k}=\left \langle f,e_{k} \right \rangle$。可这毕竟是离散化的模型，是个近似表达，如果想得到更为严格的恒等式，需要对上面的和式无限细分，并以原点对称展开，即求得其黎曼积分形式，如下 $f(t)=\int_{-\infty }^{\infty }\hat{f}(\omega)e^{2\pi i\omega t}d\omega$此即为傅里叶逆变换形式。 $\hat{f}(\omega)$是傅里叶变换，它可看成是不可数维希尔伯特空间上的正交变换 $\left ( \Im f \right )(\omega)=\hat{f}(\omega)=\int_{-\infty }^{\infty }f(t)e^{-2\pi i\varepsilon \omega t}dt$傅里叶变换，不但基底和表达式非常简单，是不可数维希尔伯特空间的正交变换（数学上的完美性），而且具有非常明晰的物理含义（表达上的直观性）。快速算法的发明使得它非常广泛的应用于光学、数字信号处理、数值模拟等领域（计算上的有效性）。在数学领域这是不多见的，是基础学术与工程的真正的完美结合。离散傅里叶变换的快速算法，看似简单，却需要深入理解傅里叶，挖掘到 $e^{-i2\pi /N}$的对称性和周期性，我想，所有的算法工程师都是梦寐以求能设计出这样的算法的。
但是，傅里叶变换对诱因稳定的，具有周期特性的信号往往有着非常好的频域特征提取能力，但不可能对所有的这样的需求都是效果好的（尤其是一些有着突变的局部特征的需求），有些特例在频域分析的时候就需要用特殊的基底，否则一些局部的重要特征就很难在频域得到很好的呈现，这推动着科学家和工程师向前探索，直到小波的发现。
小波最先在工程中应用是分析人造地震数据。事实上，人耳在初次识别声音时就已经使用了小波变换。振动波从耳鼓传到耳膜在整个耳蜗中延伸，其过程是以螺旋方式进入耳内的。假设其包络函数： $\phi (x)$，可推出（推导过程不在这里给出了，小波十讲对此有简单的表述）： $\hat{\psi}(e^{-x})=(2\pi)^{-1/2}\phi (x)$经整理可得该过程的小波基的表达式。
但是，这里的包络函数： $\phi (x)$很难简化到我们容易仿真的程度，大自然的复杂度是无限的，我们人类的认知能力永远只能逼近它的一小部分。所以说小波基的构造这样一个看似是应用的问题，可是实际上确是属于纯数学的课题。

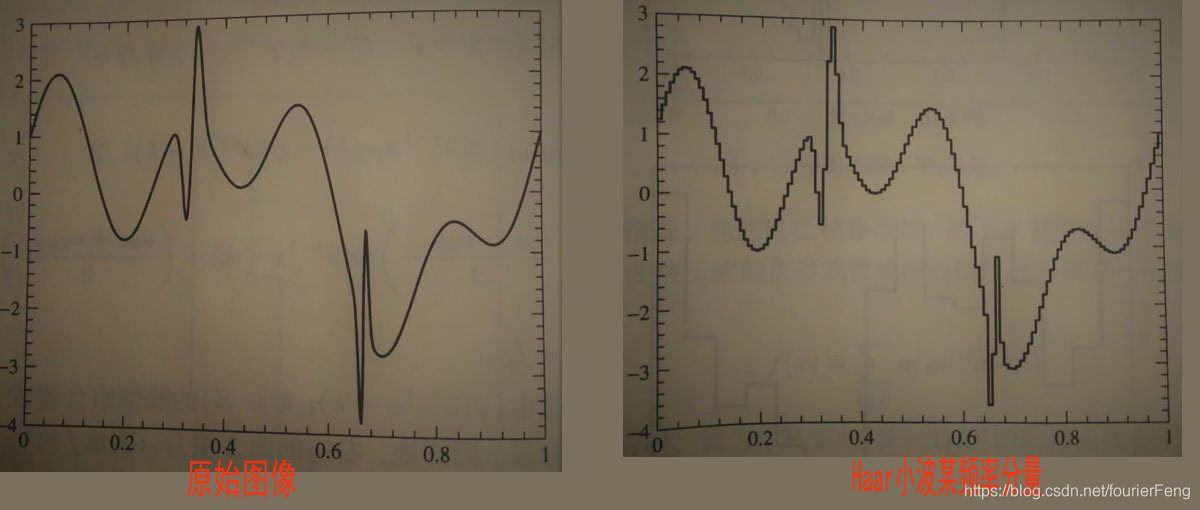
至今学术界设计小波尺度函数时考虑的仅仅是光滑度、复杂度、支集以及衰减速度（是否可用速降函数空间中的函数进行逼近）等，远没有能针对速降函数空间的某稠密子集来一一构造合适的特殊的正交小波基的能力。傅里叶变换在构造小波尺度函数的算法中依然起到了核心作用，很多年前看到过一句话：傅里叶变换是当代分析学的核心，恐怕不为过。
本人是一名热爱科学的工程师，在傅里叶中看到“美”的真正内涵，也看到了它在工程上的四两拨千斤。这样的感觉，在本人所经历的目前还是为数不多，本人这些年致力于寻找的工程与学术的美的结合，傅里叶之外，还在哪里呢？