Law of cosines or cosine formula

In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states

$c^{2}=a^{2}+b^{2}-2ab\cos \gamma ,$

where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.

Figure 1 – A triangle. The angles α (or A), β (or B), and γ(or C) are respectively opposite the sides a, b, and c.

The law of cosines generalizes the Pythagorean theorem（勾股定理）, which holds only for right triangles: if the angle γ is a right angle (of measure 90° [degrees], or π/2 radians), then cos γ = 0, and thus the law of cosines reduces to the Pythagorean theorem:

$c^{2}=a^{2}+b^{2}.$

The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.

扫描二维码关注公众号，回复： 4180934 查看本文章

Applications

The theorem is used in triangulation, for solving a triangle or circle, i.e., to find (see Figure 3):

Fig. 3 – Applications of the law of cosines: unknown side and unknown angle.

the third side of a triangle if one knows two sides and the angle between them:

$\,c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;$

the angles of a triangle if one knows the three sides:

$\,\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;$

the third side of a triangle if one knows two sides and an angle opposite to one of them (one may also use the Pythagorean theoremto do this if it is a right triangle):

$\,a=b\cos \gamma \pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.$

These formulas produce high round-off errors in floating point calculations if the triangle is very acute, i.e., if c is small relative to a and bor γ is small compared to 1. It is even possible to obtain a result slightly greater than one for the cosine of an angle.

The third formula shown is the result of solving for a in the quadratic equation a2 − 2ab cos γ + b2 − c2 = 0. This equation can have 2, 1, or 0 positive solutions corresponding to the number of possible triangles given the data. It will have two positive solutions if b sin γ < c < b, only one positive solution if c = b sin γ, and no solution if c < b sin γ or c ≥ b. These different cases are also explained by the side-side-angle congruence ambiguity.

Proofs

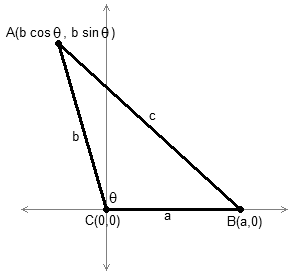
Using the distance formula

Fig. 4 – Coordinate geometry proof

Consider a triangle with sides of length a, b, c, where θ is the measurement of the angle opposite the side of length c. This triangle can be placed on the Cartesian coordinate system by plotting the following points, as shown in Fig. 4:

$A=(b\cos \theta ,b\sin \theta ),B=(a,0),{\text{ and }}C=(0,0).$

By the distance formula, we have

$c={\sqrt {(a-b\cos \theta )^{2}+(0-b\sin \theta )^{2}}}.$

Now, we just work with that equation:

${\begin{aligned}c^{2}&{}=(a-b\cos \theta )^{2}+(-b\sin \theta )^{2}\\c^{2}&{}=a^{2}-2ab\cos \theta +b^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta \\c^{2}&{}=a^{2}+b^{2}(\sin ^{2}\theta +\cos ^{2}\theta )-2ab\cos \theta \\c^{2}&{}=a^{2}+b^{2}-2ab\cos \theta .\end{aligned}}$

An advantage of this proof is that it does not require the consideration of different cases for when the triangle is acute, right, or obtuse.

Using the law of sines

By using the law of sines and knowing that the angles of a triangle must sum to 180 degrees, we have the following system of equations (the three unknowns are the angles):

${\frac {c}{\sin \gamma }}={\frac {b}{\sin \beta }},$

${\frac {c}{\sin \gamma }}={\frac {a}{\sin \alpha }},$

$\alpha +\beta +\gamma =\pi .$

Then, by using the third equation of the system, we obtain a system of two equations in two variables:

${\frac {c}{\sin \gamma }}={\frac {b}{\sin(\alpha +\gamma )}},$

${\frac {c}{\sin \gamma }}={\frac {a}{\sin \alpha }},$

where we have used the trigonometric property that the sine of a supplementary angle is equal to the sine of the angle.

Using the identity (see Angle sum and difference identities)

$\sin(\alpha +\gamma )=\sin \alpha \cos \gamma +\sin \gamma \cos \alpha$

leads to

$c(\sin \alpha \cos \gamma +\sin \gamma \cos \alpha )=b\sin \gamma ,$

$c\sin \alpha =a\sin \gamma .$

By dividing the whole system by cos γ, we have:

$c(\sin \alpha +\tan \gamma \cos \alpha )=b\tan \gamma ,$

${\frac {c\sin \alpha }{\cos \gamma }}=a\tan \gamma ,$

${\frac {c^{2}\sin ^{2}\alpha }{\cos ^{2}\gamma }}=a^{2}\tan ^{2}\gamma .$

Hence, from the first equation of the system, we can obtain

${\frac {c\sin \alpha }{b-c\cos \alpha }}=\tan \gamma$

By substituting this expression into the second equation and by using

$1+\tan ^{2}\gamma ={\frac {1}{\cos ^{2}\gamma }}$

we can obtain one equation with one variable:

$c^{2}\sin ^{2}\alpha \left(1+{\frac {c^{2}\sin ^{2}\alpha }{(b-c\cos \alpha )^{2}}}\right)=a^{2}\cdot {\frac {c^{2}\sin ^{2}\alpha }{(b-c\cos \alpha )^{2}}}$

By multiplying by (b − c cos α)2, we can obtain the following equation:

$(b-c\cos \alpha )^{2}+c^{2}\sin ^{2}\alpha =a^{2}.$

This implies

$b^{2}-2bc\cos \alpha +c^{2}\cos ^{2}\alpha +c^{2}\sin ^{2}\alpha =a^{2}.$

Recalling the Pythagorean identity, we obtain the law of cosines:

$a^{2}=b^{2}+c^{2}-2bc\cos \alpha .$

Law of cosines in non-Euclidean geometry

A version of the law of cosines also holds in non-Euclidean geometry. In spherical geometry, a triangle is defined by three points u, v, and won the unit sphere, and the arcs of great circles connecting those points. If these great circles make angles A, B, and C with opposite sides a, b, c then the spherical law of cosines asserts that both of the following relationships hold:

${\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\\cos A&=-\cos B\cos C+\sin B\sin C\cos a.\end{aligned}}$

In hyperbolic geometry, a pair of equations are collectively known as the hyperbolic law of cosines. The first is

$\cosh a=\cosh b\cosh c-\sinh b\sinh c\cos A$

where sinh and cosh are the hyperbolic sine and cosine, and the second is

$\cos A=-\cos B\cos C+\sin B\sin C\cosh a.$

As in Euclidean geometry, one can use the law of cosines to determine the angles A, B, C from the knowledge of the sides a, b, c. However, unlike Euclidean geometry, the reverse is also possible in each of the models of non-Euclidean geometry: the angles A, B, C determine the sides a, b, c.

Spherical triangle solved by the law of cosines.

https://en.wikipedia.org/wiki/Law_of_cosines