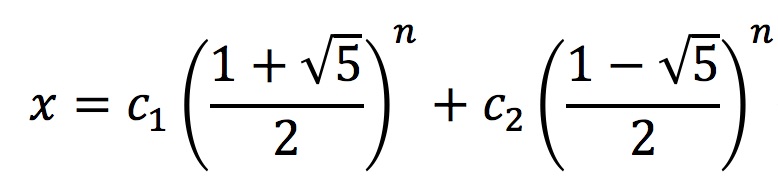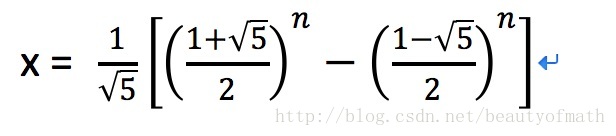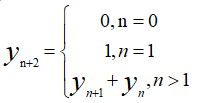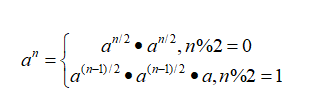目录
一、递归求解
public static int fibonacci(int x) {
if(x < 0)
throw new IllegalArgumentException("Illegal argument");
else if(x == 0)
return 1;
else if(x == 1)
return 1;
else
return fibonacci(x - 1) + fibonacci(x - 2);
}复杂度分析
设f(n)为参数为n时的时间复杂度,很明显:f(n)=f(n-1)+f(n-2) 。这就转化为了数学上的二阶常系数差分方程,并且为齐次方程。
即转化为了求f(n)的值,f(n)=f(n-1)+f(n-2)且f(0)=0; f(1)=1; 特征方程为:x^2-x-1=0 ,得 x=(1±√5)/2 。因而f(n)的通解为:
由f(0)=0; f(1)=1可解得c_1,c_2 最终可得,时间复杂度为:
解法缺点
- 递归本质是栈,当参数达到一定大小的时候栈会溢出;
- 计算fibonacci(n)就需要计算fibonacci(n-1)和fibonacci(n-2),这期间存在着大量的计算重复;
- 时间复杂度为指数级
二、解决重复计算方式
public static int fibonacci_1(int x) {
if(x < 0)
throw new IllegalArgumentException("Illegal argument");
if(x == 0)
return 0;
if(x == 1)
return 1;
int min = 0; //f(1)...
int max = 1; //f(2)...
int result = 0;
int i = 2;
while(i <= x) {
result = min + max;
min = max;
max = result;
i++;
}
return result;
}思路
从下往上计算,将中间值保存起来,避免了重复计算。
时间复杂度
O(n)
三、利用数学公式O(logn)解法
O(n)解法
斐波那契数列的递推公式:
由此可以得到
当n>=2时,上式也成立,由此得到
我们从0开始,直到n-1计算矩阵的n-1次幂,时间复杂度仍然是O(n)
public static long fibonacci_2(int x) {
if(x < 0)
throw new IllegalArgumentException("Illegal argument");
if(x == 0)
return 0;
if(x == 1)
return 1;
long[][] basicMatrix = {{1, 1},{1, 0}};
long[][] matrix = calPowerOfMatrix(basicMatrix, x - 1);
return matrix[0][0];
}
public static long[][] calPowerOfMatrix(long[][] matrix, int n){
for (int i = 0; i < n - 1; i++) {
long a = matrix[0][0];
long b = matrix[0][1];
long c = matrix[1][0];
long d = matrix[1][1];
matrix[0][0] = a + b;
matrix[0][1] = a;
matrix[1][0] = c + d;
matrix[1][1] = c;
}
return matrix;
}
O(logn)解法
乘方是具有以下性质:
可以利用这个公式使用二分法来递归实现斐波那契数列的求解,复杂度可以达到O(logn)
public static long fibonacci_3(int x) {
if(x < 0)
throw new IllegalArgumentException("Illegal argument");
if(x == 0)
return 0;
if(x == 1)
return 1;
long[][] basicMatrix = {{1, 1},{1, 0}};
long[][] matrix = calPowerOfMatrix2(basicMatrix, x - 1);
return matrix[0][0];
}
private static long[][] calPowerOfMatrix2(long[][] matrix, int n){
if(n < 0)
throw new IllegalArgumentException("Illegal argument");
if(n == 1)
return matrix;
else if(n % 2 == 0) //n为偶数,先计算矩阵的n/2次幂,再计算两个矩阵的平方
return calSquareOfMatrix((calPowerOfMatrix(matrix, n >> 1)));
else //n为奇数,先计算矩阵的(n-1)/2次幂,再计算两个矩阵的平方,再乘以一个矩阵
return calBasicMultipyOfMatrix(calSquareOfMatrix(calPowerOfMatrix(matrix, (n - 1) >> 1)));
}
private static long[][] calBasicMultipyOfMatrix(long[][] matrix){
long a = matrix[0][0];
long b = matrix[0][1];
long c = matrix[1][0];
long d = matrix[1][1];
matrix[0][0] = a + b;
matrix[0][1] = a;
matrix[1][0] = c + d;
matrix[1][1] = c;
return matrix;
}
private static long[][] calSquareOfMatrix(long[][] matrix){
long a = matrix[0][0];
long b = matrix[0][1];
long c = matrix[1][0];
long d = matrix[1][1];
matrix[0][0] = a*a + b*c;
matrix[0][1] = a*b + b*d;
matrix[1][0] = a*c + c*d;
matrix[1][1] = b*c + d*d;
return matrix;
}参考