前言
本文主要记录在凸优化中几个比较基础的概念:凸集、仿射集、凸包、锥、锥包。
仿射集(affine sets)
回顾一下直线与线段的定义。
对于
\[x_1 \not = x_2 \in R^n, \theta \in R\]
则直线可以表示为:
\[y = \theta x_1 + (1-\theta)x_2\]
类似的,对\(\theta\)加一点限制,就可以导出线段的定义:
\[y = \theta x_1 + (1-\theta)x_2, \theta \in R, \theta \in [0,1]\]
有了直线的概念后,下面定义仿射集:
- 仿射集:一个集合\(C\)是仿射集,若\(\forall x_1,x_2 \in C\),则连接\(x_1\)与\(x_2\)的直线也在集合内。
用数学的语言来描述的话就是:
- 仿射集:设\(x_1, ..., x_k \in C, \theta_1, ..., \theta_k \in R, \theta_1 + ... + \theta_k = 1\),如果集合\(C\)是仿射集,当且仅当\(\theta_1 x_1 + ... + \theta_k x_k \in C\)
我们把 \(\theta_1 x_1 + ... + \theta_k x_k\)叫做仿射组合。
与C相关的子空间
下面讲一下仿射集的一些性质。根据上面的定义,若\(x_1, x_2 \in C\), \(C\)是仿射集,则\(\theta x_1 + (1-\theta) x_2 \in C\),其中\(\theta \in R\)。那么问,\(\alpha x_1 + \beta x_2\)是否属于\(C\)呢?
如下图所示,当直线不经过原点时,显然\(\alpha x_1 + \beta x_2 \not \in C\),当直线经过原点时,就有\(\alpha x_1 + \beta x_2 \in C\)。
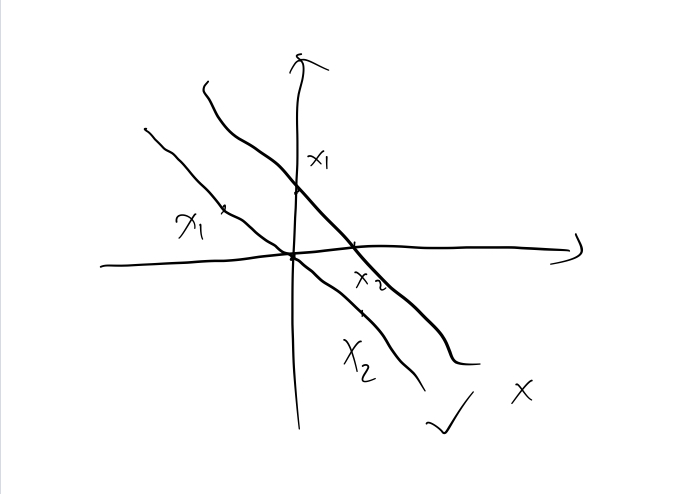
我们定义:\(V = C - v_0 = \{x-x_0|x \in C\}, \forall x_0 \in C\)
称\(V\)为与\(C\)相关的子空间。我们可以理解成\(V\)是\(C\)平移\(v_0\)得到的一个字空间。
证:
\[\forall v_1, v_2 \in C, \forall \alpha, \beta \in R\]
因为\(v_1 + v_0 \in C, v_2 + x_0 \in C, x_0 \in C\), 所以:
\[\alpha (v_1+x_0) + \beta (v_2+x_0) + (1-\alpha - \beta) x_0 \in C\]
即
\[\alpha v_1 + \beta v_2 + x_0 \in C\]
此时就有:
\[\alpha v_1 + \beta v_2 \in V\]
一个例子
- 线性方程组的解集是仿射集
\[C = \{x|AX=b\}, A \in R^{m \times n}, b \in R^m, x \in R^n\]
与\(C\)相关的子空间\(V=\{x - x_0| x \in C\}, \forall x_0 \in C\) 恰好也是矩阵\(A\)的零空间。
仿射包
对于任意一个集合\(C\),是否可以构造出其最小的仿射集。如果可以,这个最小的仿射集就叫做仿射包。
仿射包:\(aff\ C = \{\theta_1 x_1 + ... + \theta_k x_k | \forall x_1,...,x_k \in C, \theta_1+\theta_2+...+\theta_k = 1\}\)
仿射集的仿射包就是它本身。
凸集 Convex Set
- 一个集合是凸集,即当任意两点之间的线段任然在\(C\)内
- 用数学表达的话就是:\(\forall x_1, x_2 \in C, \forall \theta, \theta \in [0,1], \theta x_1 + (1-\theta) x_2 \in C\)
\(x_1, ..., x_k\)的凸组合
\(x_1, ..., x_k\)的凸组合表示为:
\[\theta_1 x_1 + \theta_2 x_2 + ... + \theta_k x_k \in C\]
\[\theta_1, ... ,\theta_k \in R, \theta_1+...+\theta_k = 1\]
\[ \theta_1,...,\theta_k \in [0,1]\]
- \(C\)为凸集等价于任意\(C\)的凸组合也在\(C\)内。
凸包
对任意集合\(C \in R^n\),它的凸包记作:
\[Cov C = \{\theta_1 x_1 + ..., + \theta_k x_k | \forall x1, ..., x_k \in C, \forall \theta_1,...\theta_k \in [0,1], \theta_1+...+\theta_k=1\}\]
锥 Cone 和 凸锥 Convex Cone
- \(C\)是锥等价于 \(\forall x \in C, \theta > 0\),有\(\theta x \in C\)
- \(C\)是凸锥等价于 \(\forall x_1, x_2 \in C, \theta_1, \theta_2 \geq 0\),有\(\theta_1 x_1 + \theta_2 x_2 \in C\)
凸锥的组合
\[\theta_1 x_1 + ... + \theta_k x_k, \theta_1,...,\theta_k \geq 0\]
凸锥包
\[x_1,...,x_k \in C, \{\theta_1 x_1 + ... + \theta_k x_k | x_1,...,x_k \in C, \theta_1,...,\theta_k \geq 0\}\]
总结
仿射组合
\[\forall \theta_1, ..., \theta_k, \theta_1+...+\theta_k = 1\]凸组合
\[\theta_1,...,\theta_k, \theta_1 + ...+\theta_k = 1, \theta_1,...,\theta_k \in [0,1]\]凸锥组合
\[\forall \theta_1,...\theta_k, \theta_1,...,\theta_k \geq 0\]- 任意一个仿射集,它一定是凸的。
- 凸锥也一定是凸的。
- 如果集合只有一个元素:\(C={x}\),该集合也是一个仿射集。若这个点是原点,即\(x=0\),那么它还是凸锥。
空集也是仿射集,同时还是凸集和凸锥。