【CodeForces】CodeForces Round #475 (Div. 1 + Div. 2) 题解

【比赛链接】

Div. 1

Div. 2

【题解链接】

点击打开链接

【Div.2 A】Splits

【思路要点】

由于我们希望得到尽可能不同的权值，我们可以考虑在拆分的开头放置若干个2，然后放1填补剩余的数字。

不难发现答案等于\(\lfloor\frac{N}{2}\rfloor+1\)。

时间复杂度\(O(1)\)。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int main() {
	int n; read(n);
	writeln(n / 2 + 1);
	return 0;
}

【Div.2 B】Messages

【思路要点】

考虑到阅读信息的收益是关于时间的一次函数，最值一定可以在端点处取到。

在收到信息立刻阅读与留到最后阅读两个方案中取较大者即可。

时间复杂度\(O(N)\)。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int main() {
	int n, A, B, C, T, ans = 0;
	read(n), read(A), read(B), read(C), read(T);
	for (int i = 1; i <= n; i++) {
		int x; read(x);
		ans += A;
		if (C >= B) ans += (T - x) * (C - B);
	}
	writeln(ans);
	return 0;
}

【Div.2 C/Div.1 A】Alternating Sum

【思路要点】

不难发现数列每\(K\)项的和形成了一个等比数列，公比为\(\frac{b^K}{a^K}\)。

暴力算出前\(K\)项的和，求这个等比数列的和即可，注意特判公比为1的情况。

时间复杂度\(O(KLogN)\)。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
const int P = 1e9 + 9;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
long long power(long long x, long long y) {
	if (y == 0) return 1;
	long long tmp = power(x, y / 2);
	if (y % 2 == 0) return tmp * tmp % P;
	else return tmp * tmp % P * x % P;
}
char s[MAXN];
long long n, a, b, k, first, r;
int main() {
	read(n), read(a), read(b), read(k);
	scanf("%s", s);
	for (int i = 0; i <= k - 1; i++) {
		if (s[i] == '+') first += power(a, n - i) * power(b, i) % P;
		if (s[i] == '-') first -= power(a, n - i) * power(b, i) % P;
	}
	first = (first % P + P) % P;
	r = power(b * power(a, P - 2) % P, k);
	n = (n + 1) / k;
	if (r == 1) writeln(first * n % P);
	else writeln((first * (power(r, n) - 1) % P) * power(r - 1, P - 2) % P);
	return 0;
}

【Div.2 D/Div.1 B】Destruction of a Tree

【思路要点】

首先，叶子结点不可能被首先摧毁，一定需要等它的父亲被摧毁后，叶子结点才能够被摧毁。

考虑一个DFS的过程，对于节点\(i\)，其父亲是否在其之前摧毁会对其在被摧毁时的度数产生1的影响，恰有一种情况会使得其能够被摧毁。如果该点需要在父亲前被摧毁，那么将其摧毁，并删去其与父亲的连边；否则保留其与父亲的连边，在其父亲被摧毁后摧毁之。

有解的条件是根节点可以被摧毁，具体细节读者可阅读代码加以理解。

时间复杂度\(O(N)\)。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 200005;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
vector <int> a[MAXN], b[MAXN];
int tot, ans[MAXN];
void finish(int pos) {
	ans[++tot] = pos;
	for (unsigned i = 0; i < b[pos].size(); i++)
		finish(b[pos][i]);
}
int work(int pos, int fa) {
	int degree = fa != 0;
	for (unsigned i = 0; i < a[pos].size(); i++)
		if (a[pos][i] != fa) degree += work(a[pos][i], pos);
	if (degree % 2 == 0) {
		finish(pos);
		return 0;
	} else {
		b[fa].push_back(pos);
		return 1;
	}
}
int main() {
	int n; read(n);
	for (int i = 1; i <= n; i++) {
		int x; read(x);
		if (x != 0) {
			a[x].push_back(i);
			a[i].push_back(x);
		}
	}
	if (work(1, 0)) printf("NO\n");
	else {
		printf("YES\n");
		for (int i = 1; i <= n; i++)
			writeln(ans[i]);
	}
	return 0;
}

【Div.2 E/Div.1 C】Cutting Rectangle

【思路要点】

设原矩形被分成了\(q\)行\(p\)列，共分成了\(S\)个小矩形，显然有\(p*q=S\)，即\(p\ |\ S\)且\(q=\frac{S}{p}\)。

考虑长为\(i\)的所有矩形，设每一种长为\(i\)的矩形个数的总数为\(sum(x=i)\)的最大公约数为\(gcd(x=i)\)。

那么，应当有\(p\ |\ sum(x=i)\)，并且，所有长为\(i\)的所有矩形将分成\(\frac{sum(x=i)}{p}\)行，这个行数应当被每一种长为\(i\)的矩形个数整除，即\(\frac{sum(x=i)}{p}\ |\ gcd(x=i)\)，并且此时，每一行放置的矩形种类和个数均已确定，因此，原矩形的宽是确定的。

类似地，也应当有\(q\ |\ sum(y=i)\)以及\(\frac{sum(y=i)}{q}\ |\ gcd(y=i)\)，也即\(S\ |\ sum(y=i)*p\)以及\(p*sum(y=i)\ |\ gcd(y=i)*S\)，同时我们发现，此时每一列放置的矩形种类和个数均已确定，因此，原矩形的长也是确定的。

因此，一个合法的\(p\)对应一个唯一的原问题的解，问题等价于求出合法的\(p\)的个数。

上面对\(p\)的限制可以合并为\(A\ |\ p\)且\(p\ |\ B\)，那么答案即为\(\frac{B}{A}\)的约数个数。

时间复杂度\(O(NLogN+\sqrt{S})\)。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 200005;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
long long getgcd(long long x, long long y) {
	if (x == 0 || y == 0) return x + y;
	else return getgcd(y, x % y);
}
struct info {long long x, y, cnt; };
bool cmpx(info a, info b) {return a.x < b.x; }
bool cmpy(info a, info b) {return a.y < b.y; }
info a[MAXN];
long long s, l, r;
long long f(long long x) {
	long long i = 2, ans = 1;
	while (i * i <= x) {
		int cnt = 1;
		while (x % i == 0) {
			x /= i;
			cnt++;
		}
		ans *= cnt;
		i++;
	}
	if (x != 1) ans *= 2;
	return ans;
}
int main() {
	int n; read(n);
	s = 0, l = 1;
	for (int i = 1; i <= n; i++)
		read(a[i].x), read(a[i].y), read(a[i].cnt), s += a[i].cnt;
	r = s;
	sort(a + 1, a + n + 1, cmpx);
	for (int i = 1; i <= n; i++)
		if (a[i].x != a[i - 1].x) {
			long long sum = 0, gcd = 0;
			for (int j = i; a[j].x == a[i].x; j++) {
				sum += a[j].cnt;
				gcd = getgcd(gcd, a[j].cnt);
			}
			r = getgcd(r, sum);
			long long now = sum / gcd;
			long long tmp = getgcd(now, l);
			now /= tmp;
			if (l > r / now) {
				printf("0\n");
				return 0;
			} else l *= now;
		}
	sort(a + 1, a + n + 1, cmpy);
	for (int i = 1; i <= n; i++)
		if (a[i].y != a[i - 1].y) {
			long long sum = 0, gcd = 0;
			for (int j = i; a[j].y == a[i].y; j++) {
				sum += a[j].cnt;
				gcd = getgcd(gcd, a[j].cnt);
			}
			long long tmp = s / getgcd(s, sum), tnp = getgcd(tmp, l);
			tmp /= tnp;
			if (l > r / tmp) {
				printf("0\n");
				return 0;
			} else l *= tmp;
			long long now = sum / gcd;
			if (s % now != 0) {
				printf("0\n");
				return 0;
			}
			now = s / now;
			r = getgcd(now, r);
		}
	if (r % l != 0) printf("0\n");
	else printf("%lld\n", f(r / l));
	return 0;
}

【Div.1 D】Frequency of String

【思路要点】

注意到一个关键的条件是询问串不会重复出现。

不同的询问串长度只会出现至多\(O(\sqrt{N})\)个，而长度相同的询问串的总出现次数不超过\(N\)，因此所有询问串的总出现次数是\(O(N\sqrt{N})\)的，因此我们只需要找到每个询问串出现的位置，排序+扫描即可得到答案。

查找询问串的出现位置显然可以通过后缀树实现。

时间复杂度\(O(N\sqrt{N}LogN)\)，常数很小。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 200005;
const int MAXC = 26;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
struct SuffixAutomaton {
	int root, size, last;
	int child[MAXN][MAXC];
	int fail[MAXN], depth[MAXN], num[MAXN];
	vector <int> a[MAXN];
	int newnode(int dep) {
		fail[size] = 0;
		depth[size] = dep;
		memset(child[size], 0, sizeof(child[size]));
		return size++;
	}
	void extend(int ch, int pos) {
		int p = last, np = newnode(depth[last] + 1);
		while (child[p][ch] == 0) {
			child[p][ch] = np;
			p = fail[p];
		}
		if (child[p][ch] == np) fail[np] = root;
		else {
			int q = child[p][ch];
			if (depth[q] == depth[p] + 1) fail[np] = q;
			else {
				int nq = newnode(depth[p] + 1);
				fail[nq] = fail[q];
				fail[q] = fail[np] = nq;
				memcpy(child[nq], child[q], sizeof(child[q]));
				while (child[p][ch] == q) {
					child[p][ch] = nq;
					p = fail[p];
				}
			}
		}
		num[last = np] = pos;
	}
	void init(char *s) {
		size = 0;
		root = last = newnode(0);
		int len = strlen(s + 1);
		for (int i = 1; i <= len; i++)
			extend(s[i] - 'a', i);
		for (int i = 1; i < size; i++)
			a[fail[i]].push_back(i);
	}
	int tot, pos[MAXN];
	void dfs(int root) {
		if (num[root]) pos[++tot] = num[root];
		for (unsigned i = 0; i < a[root].size(); i++)
			dfs(a[root][i]);
	}
	int query(int cnt, char *s) {
		int now = root, len = strlen(s + 1);
		for (int i = 1; i <= len; i++)
			if (child[now][s[i] - 'a']) now = child[now][s[i] - 'a'];
			else return -1;
		tot = 0; dfs(now);
		if (tot < cnt) return -1;
		sort(pos + 1, pos + tot + 1);
		int ans = MAXN;
		for (int i = cnt; i <= tot; i++)
			chkmin(ans, pos[i] - pos[i - cnt + 1]);
		return ans + len;
	}
} SAM;
char s[MAXN], t[MAXN];
int main() {
	scanf("%s", s + 1);
	SAM.init(s);
	int q; read(q);
	for (int i = 1; i <= q; i++) {
		int cnt;
		scanf("%d %s", &cnt, t + 1);
		writeln(SAM.query(cnt, t));
	}
	return 0;
}

【Div.1 E】Circles of Waiting

【思路要点】

显然有朴素的\(O(R^6)\)的高斯消元。

考虑按照从上到下，从左到右的顺序进行消元，每次只对当前行非0的位置进行减法，并且若某一行当前元系数为0，则不对其进行减法，这样的时间复杂度是\(O(R^4)\)的。

我们来证明这一点。

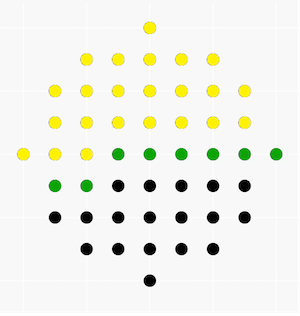
上图中，黄色代表结束消元的位置，绿色代表与黄色相邻的位置，黑色代表其他位置。

我们当前处理的是某一个绿色的元素，它的方程中不会含有黄色的未知数，只会含有绿色的\(O(R)\)个未知数以及\(O(1)\)个初始时与其相邻的黑色的未知数，不难发现这个方程系数非零的位置只有\(O(R)\)个。

并且，含有当前未知数的方程同样只有\(O(R)\)个，因此处理每一个方程我们花费的时间是\(O(R^2)\)的，总时间复杂度自然为\(O(R^4)\)。

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 8005;
const int MAXM = 120;
const int MAXR = 60;
const int P = 1e9 + 7;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int power(int x, int y) {
	if (y == 0) return 1;
	int tmp = power(x, y / 2);
	if (y % 2 == 0) return 1ll * tmp * tmp % P;
	else return 1ll * tmp * tmp % P * x % P;
}
int n, p[5], point[MAXM][MAXM], a[MAXN][MAXN];
int main() {
	int r; read(r);
	for (int i = 1; i <= 4; i++) {
		read(p[i]);
		p[0] += p[i];
	}
	for (int i = 1; i <= 4; i++)
		p[i] = 1ll * p[i] * power(p[0], P - 2) % P;
	for (int i = -r; i <= r; i++)
	for (int j = -r; j <= r; j++) {
		int tmp = i * i + j * j;
		if (tmp <= r * r) point[i + MAXR][j + MAXR] = ++n;
	}
	for (int i = -r + MAXR; i <= r + MAXR; i++)
	for (int j = -r + MAXR; j <= r + MAXR; j++) {
		if (point[i][j] == 0) continue;
		int tmp = point[i][j];
		a[tmp][tmp] = P - 1; a[tmp][n + 1] = P - 1;
		if (point[i - 1][j] != 0) a[tmp][point[i - 1][j]] = p[1];
		if (point[i][j - 1] != 0) a[tmp][point[i][j - 1]] = p[2];
		if (point[i + 1][j] != 0) a[tmp][point[i + 1][j]] = p[3];
		if (point[i][j + 1] != 0) a[tmp][point[i][j + 1]] = p[4];
	}
	for (int i = 1; i <= n; i++) {
		for (int j = i; j <= n + 1; j++)
			if (a[j][i] != 0) {
				swap(a[i], a[j]);
				break;
			}
		int top = 0;
		static int q[MAXN];
		for (int j = 1; j <= n + 1; j++)
			if (a[i][j] != 0) q[++top] = j;
		int inv = power(a[i][i], P - 2);
		for (int j = 1; j <= top; j++)
			a[i][q[j]] = 1ll * a[i][q[j]] * inv % P;
		for (int j = i + 1; j <= n; j++) {
			if (a[j][i] == 0) continue;
			int tmp = a[j][i];
			for (int k = 1; k <= top; k++)
				a[j][q[k]] = (a[j][q[k]] - 1ll * tmp * a[i][q[k]] % P + P) % P; 
		}
	}
	for (int i = n; i >= 1; i--) {
		for (int j = i + 1; j <= n; j++)
			a[i][n + 1] = (a[i][n + 1] - 1ll * a[j][0] * a[i][j] % P + P) % P;
		a[i][0] = 1ll * a[i][n + 1] * power(a[i][i], P - 2) % P;
		if (i == point[MAXR][MAXR]) {
			writeln(a[i][0]);
			return 0;
		}
	}
	return 0;
}

【CodeForces】CodeForces Round #475 (Div. 1 + Div. 2) 题解

猜你喜欢