2022 Huashu Cup Paper Ideas Analysis + Complete Code (Montageplan für Unterwasserroboter)

Sie können sich das offizielle Analysevideo ansehen (solange dieses Video ein Kandidat ist, können Sie es kostenlos ansehen. Für diejenigen, die es nicht sehen können, werde ich in ein paar Tagen einen Blog erstellen). , ich habe die offizielle Standardantwort an das Ende dieses Blogs gestellt, für Ihre eigene Referenz.
Offizielles Analysevideo zum Huashu Cup 2022 zu Frage B》》》》》》》

Hier ist eine Aussage, ich nehme mit der C-Frage am Huashu Cup teil. Die These und der Code beziehen sich auf andere, aber es ist tatsächlich dieser Blog, an dessen Klärung ich so hart gearbeitet habe. Ich bin auch ein Anfänger, und ich Ich habe es nur zum Sortieren verschickt. Die Ideen eignen sich zum Selbstlernen und dienen nur als Referenz. Es gibt keine hervorragende Arbeit oder eine Standardantwort.

Vollständiger Titel:
Link: https://pan.baidu.com/s/16E1X35O13NWIij72OClVgQ?pwd=1234
Extraktionscode: 1234

1. Das Thema

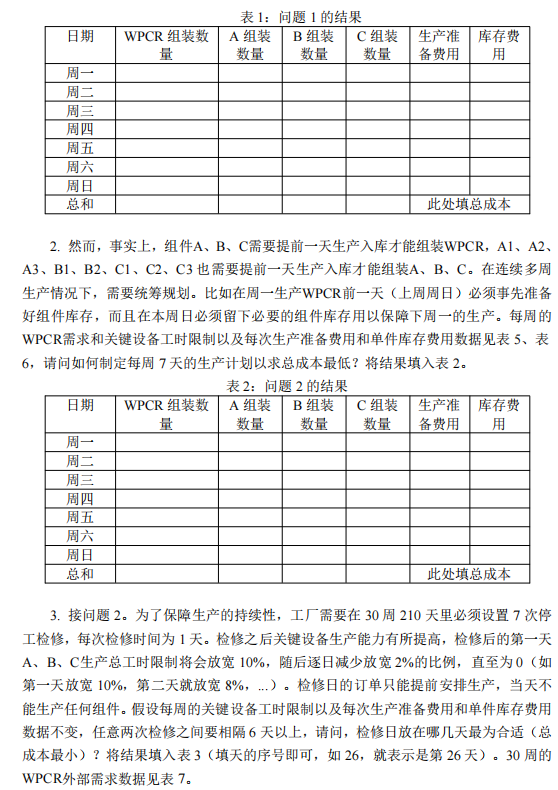
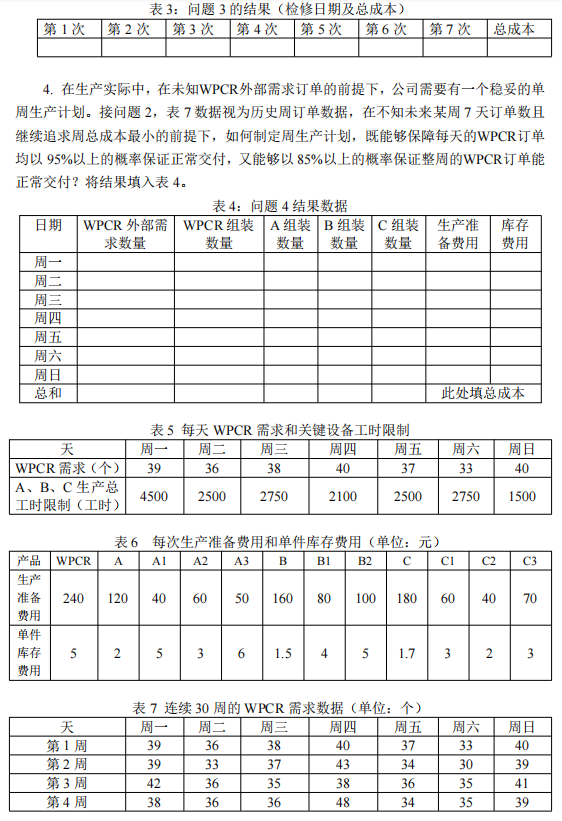
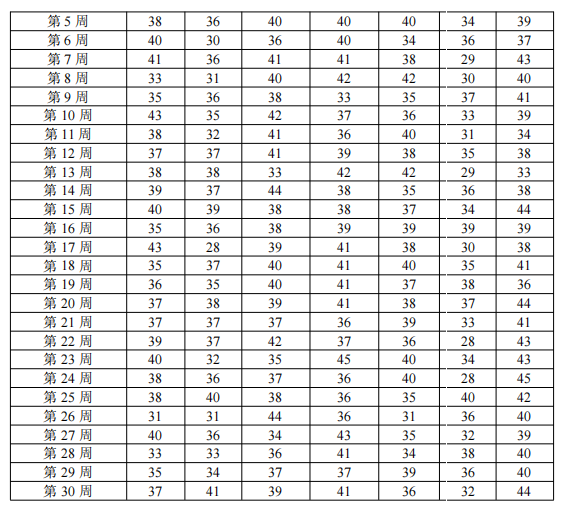
2. Problemanalyse

3. Modellannahmen

1. Ausreichende Materialien für die Montage kleiner Komponenten.
2. Während des Produktionsprozesses wird die Produktion nicht durch unerwartete Situationen wie Stromausfälle in der Fabrik und mechanische Fehler unterbrochen.
3. Der Kapitalfluss der Fabrik ist normal und die Produktion wird nicht durch Kapitalmangel beeinträchtigt.
4. Nur das Endprodukt Roboter hat externe Nachfrage und andere Komponenten werden nicht extern verkauft.
5. Die Nachfrage nach Robotern wird planmäßig bestimmt und ist nicht von Marktpreisschwankungen betroffen.

4. Symbolbeschreibung

Symbol	veranschaulichen	Einheit
d	Tage	Himmel
MA1 d , MA2 d , MA3 d … MC3 d	Widget-Montagemenge am Tag d	individuell
SA1 d , SA2 d , SA3 d … SC3 d	Restmenge des Widgets am Tag d	individuell
MA d , MB d , MC d	Montagemenge von Großkomponenten am Tag d	individuell
SA d , SB d ,SC d	Restmenge Großkomponenten am Tag d	individuell
DWd	Die Anzahl der am Tag d angeforderten Roboter	individuell
MW d	Die Anzahl der am Tag d montierten Roboter	individuell
SW d	Die verbleibende Anzahl von Robotern am Tag d	individuell
T d	Gesamtarbeitszeitgrenze am Tag d	Arbeitszeit
RA1,RA2,…RB,RC	Lagerkosten pro Einheit für die Komponente	Yuan
FA1,FA2,…,FB,FC	Produktionsvorbereitungskosten des Bauteils	Yuan
XW d	0-1 Variable, ob am Tag d Roboter produziert werden sollen	-
R d	Bestandskosten am Tag d	Yuan
F d	Produktionsvorbereitungskosten am Tag d	Yuan
checkDatum t	Datum der t-ten Revision	Himmel
Tbig d	Gesamtarbeitszeitgrenze am Tag d	Arbeitszeit
DWpredict d	Die Anzahl der Roboter, die am d-ten Tag einer Woche in der Zukunft angefordert werden	individuell

5. Erstellung und Lösung von Problem 1 Modell

5.1 Die Etablierung des Problemmodells

5.1.1 Kleine Bauteile bauen große Bauteile zusammen

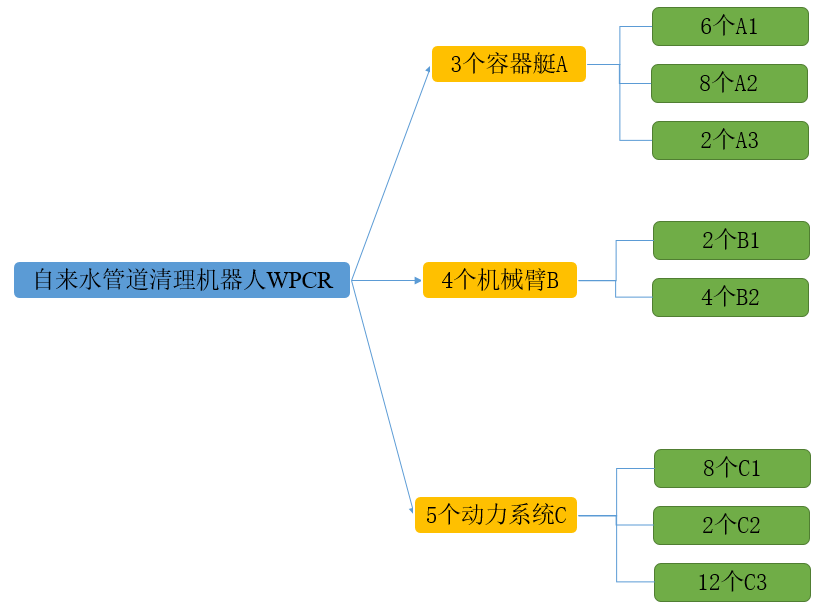
Hier wird als Beispiel die Montage des großen Bauteils A genommen. Der Zusammenbau einer großen Komponente A erfordert 6 kleine Komponenten A1, 8 kleine Komponenten A2 und 2 kleine Komponenten A3.

Am Tag d beträgt die Anzahl der kleinen Komponenten A1, die zum Zusammenbau der großen Komponente A verwendet wurden: die Anzahl der am Tag d (dem aktuellen Tag) montierten kleinen Komponenten MA1 _d und die Anzahl der am Tag d-1 (gestern) verbleibenden kleinen Komponenten SA1 _d-1 und nämlich MA1 _d + SA1 _d-1 . Die Anzahl der Widgets A2 und A3 kann auf die gleiche Weise erhalten werden.

Die Montage einer großen Komponente A erfordert 6 kleine Komponenten A1. Wenn nur A1 berücksichtigt wird, beträgt die maximale Anzahl an großen Komponenten, die montiert werden können:

$$\left[\begin{array}{c}\frac{MA1\_{}_{}+SA1\_{}_{d-}}{6}\end{array}\right]\text{\hspace{1em}( 1 )}$$

Hinweis: Das Symbol [ ] wird hier abgerundet, d. h. die größte ganze Zahl kleiner als sich selbst nehmen.

Wenn nur A2 betrachtet wird, beträgt die maximale Anzahl von großen Komponenten A, die zusammengebaut werden können, in ähnlicher Weise:

$$\left[\begin{array}{c}\frac{MA2\_{}_{}+SA2\_{}_{d-}}{8}\end{array}\right]\text{\hspace{1em}( 2 )}$$
Wenn nur A3 betrachtet wird, beträgt die maximale Anzahl von großen Komponenten A, die zusammengebaut werden können:

$$\left[\begin{array}{c}\frac{MA3\_{}_{}+SA3\_{}_{d-}}{2}\end{array}\right]\text{\hspace{1em}( 3 )}$$

Daher beträgt die maximale Anzahl an Baugruppen des Großbauteils A am Tag d:

$$Mindest\left[\left(\begin{array}{c}\frac{MA1\_{}_{}+SA1\_{}_{d-}}{6},\frac{MA2\_{}_{}+SA2\_{}_{d-}}{8},\frac{MA3\_{}_{}+SA3\_{}_{d-}}{2}\end{array}\right)\right]\text{\hspace{1em}( 4 )}$$

Hinweis: Dies muss abgerundet werden

Die Anzahl der für jeden Tag erforderlichen Roboter ist unterschiedlich.Um den Bedarf des Auftrags zu erfüllen, wenn die Fabrik die große KomponenteA montiert, muss sie nicht unbedingt gleich dem Maximalwert sein. Daher sollte die Montagemenge der großen Komponente A am Tag d die folgenden Randbedingungen erfüllen:

$$MA{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MA1\_{}_{}+SA1\_{}_{d-}}{6},\frac{MA2\_{}_{}+SA2\_{}_{d-}}{8},\frac{MA3\_{}_{}+SA3\_{}_{d-}}{2}\end{array}\right)\right]\text{\hspace{1em}( 5 )}$$

In gleicher Weise sollte am d-Tag die Montagemenge der großen Komponenten B und C die folgenden Einschränkungen erfüllen:

$$MB{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MB1{\_}_{}+SB1{\_}_{d-}}{2},\frac{MB2{\_}_{}+SB2{\_}_{d-}}{4}\end{array}\right)\right]\text{\hspace{1em}( 6 )}$$

$$MC{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MC{1}_{}+SC1{\_}_{d-}}{8},\frac{MC{2}_{}+SC2{\_}_{d-}}{2},\frac{MC{2}_{}+SC2{\_}_{d-}}{12}\end{array}\right)\right]\text{\hspace{1em}( 6 )}$$

5.1.2 Verbleibende Widgets

Nach dem Zusammenbau einer großen Komponente mit einer kleinen Komponente können Reste der kleinen Komponente vorhanden sein. Hier wird das Widget A1 als Beispiel verwendet.
Am Tag d muss die verbleibende Anzahl von Artikeln A1 die Summe der Anzahl von Artikeln erfüllen, die am Tag d MA1 _d zusammengestellt wurden, und die Anzahl von Artikeln, die am Tag d-1 SA1 _d-1 verbleiben , abzüglich der Summe der Anzahl von Widgets am Tag d d-1 Der Verbrauch von Al. Um ein großes Bauteil A zusammenzubauen, werden 6 kleine Bauteile A1 benötigt. Daher beträgt die Verbrauchsmenge von Al am Tag d 6 × MA _d . Daher ist die Restmenge SA1 _d von A1 am Tag d wie folgt:

$$SA{1}_{}=MA1\_{}_{}+SA{1}_{d-}-6\ast MA{\_}_{}\text{\hspace{1em}( 7 )}$$

Heute – verbraucht = verbleibend
(heutiges Zusammengebautes + gestern übrig gebliebenes) – verbraucht = verbleibend

Die verbleibende Anzahl weiterer kleiner Komponenten erhält man auf die gleiche Weise:
$$SA{2}_{}=MA2\_{}_{}+SA{2}_{d-}-8\ast MA{\_}_{}$$
$$SA{3}_{}=MA3\_{}_{}+SA{3}_{d-}-2\ast MA{\_}_{}$$
$$SB1{\_}_{}=MB1{\_}_{}+SB1{\_}_{d-}-2\ast MB{\_}_{}$$
$$SB2{\_}_{}=MA1\_{}_{}+SA{1}_{d-}-4\ast MB{\_}_{}\text{\hspace{1em}( 8 )}$$
$$SC1{\_}_{}=MC{1}_{}+SC1{\_}_{d-}-8\ast MC{\_}_{}$$
$$SC2{\_}_{}=MC{2}_{}+SC2{\_}_{d-}-2\ast MC{\_}_{}$$
$$SC{3}_{}=MC{3}_{}+SC{3}_{d-}-12\ast MC{\_}_{}$$

5.1.3 Berechnung der verbleibenden Großbauteile durch die Bestückungsmenge des Roboters

Die Montage des Roboters, d.h. die Montage des Roboters mit großen Komponenten, ist die gleiche wie die Montage großer Komponenten mit kleinen Komponenten. Daher ist die Anzahl der am d-Tag montierten Roboter wie folgt:

$$MW{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MA1\_{}_{}+SA1\_{}_{d-}}{3},\frac{MB2{\_}_{}+SB2{\_}_{d-}}{4},\frac{MC{2}_{}+SC2{\_}_{d-}}{5}\end{array}\right)\right]\text{\hspace{1em}( 9 )}$$

Darunter ist MW _d die Anzahl der montierten Roboter, MA _d die Montageanzahl der großen Komponenten A am Tag d und SA _d-1 die verbleibende Anzahl der großen Komponenten A am Tag d-1.

Bauen Sie den Roboter aus großen Komponenten zusammen, die einige Reste haben können. Sie wird auf die gleiche Weise wie die Berechnung der verbleibenden Anzahl von Widgets wie folgt berechnet:

$$S{A}_{}=MA{\_}_{}+S{A}_{d-}-3\ast MW{\_}_{}$$
$$S{B}_{}=MB{\_}_{}+S{B}_{d-}-4\ast MW{\_}_{}\text{\hspace{1em}( 10 )}$$
$$S{C}_{}=MC{\_}_{}+S{C}_{d-}-5\ast MW{\_}_{}$$

5.1.4 Mengenbeschränkungen für die Robotermontage

Alle vom Werk angenommenen Roboteraufträge müssen nach Ablauf geliefert werden, daher sollte die Summe aus der Montagemenge MW _d der Roboter am Tag d und der Restmenge SW _d der Roboter am Tag d-1 größer sein als die Bedarfsmenge DW d am Tag _d .
$$MW{\_}_{}+S{W}_{d-}⩾D{W}_{}\text{\hspace{1em}( 12 )}$$

5.1.5 Verbleibender Roboter

Nach dem täglichen Verkauf von Bots auf Bestellung können einige Reste übrig bleiben. Die Restmenge SW _d des Roboters am Tag d ist gleich der Summe der Montagemenge MW _d am Tag d und der Restmenge SW _d-1 am Tag d-1 abzüglich der Auftragsmenge DW _d am Tag . welches ist

$$S{W}_{}=MW{\_}_{}+S{W}_{d-}-D{W}_{}\text{\hspace{1em}( 12 )}$$

5.1.6 Kein Bestand Kein Restbestand

Tag 1 beginnt ohne vorrätige Komponenten, dh:
$$SA{1}_{}=SA{2}_{}=SA{3}_{}=SB1{\_}_{}=SB2{\_}_{}=SC1{\_}_{}=SC2{\_}_{}=SC{3}_{}\text{\hspace{1em}( 13 )}$$
$$S{A}_{}=S{B}_{}=S{C}_{}=0\text{\hspace{1em}( 13 )}$$

Nach dem siebten Tag, d. h., wird kein Komponentenbestand mehr gelassen.

$$SA{1}_{}=SA{2}_{}=SA{3}_{}=SB1{\_}_{}=SB2{\_}_{}=SC1{\_}_{}=SC2{\_}_{}=SC{3}_{}$$
$$S{A}_{}=S{B}_{}=S{C}_{}=0\text{\hspace{1em}( 14 )}$$
$$S{W}_{}=0$$

5.1.7 Arbeitszeitbeschränkungen

Es dauert 3 Arbeitsstunden, um 1 Stück A herzustellen, 5 Arbeitsstunden, um 1 Stück B herzustellen, und 5 Arbeitsstunden, um 1 Stück C herzustellen. Die folgenden Einschränkungen müssen gleichzeitig erfüllt werden:

$$3\times MA{\_}_{}+5\times MB{\_}_{}+5\times MC{\_}_{}⩽T_{}\text{\hspace{1em}( 15 )}$$

5.1.8 Inventargebühr

Wenn eine Komponente am Ende eines Tages auf Lager ist, muss die Fabrik eine bestimmte Bestandsgebühr zahlen, die proportional zur verbleibenden Menge der Komponente ist. Daher können gemäß der verbleibenden Menge an Komponenten am d-Tag die Bestandskosten von kleinen Komponenten, großen Komponenten und Robotern ausgedrückt werden.

$$RkleinA\_\_{}_{}=RA1\_\times SA{1}_{}+RA2\_\times SA{2}_{}+RA3\_\times SA{3}_{}$$

$$Rsmall{B}_{}=RB1\_\times SB1{\_}_{}+RB2\_\times SB2{\_}_{}$$

$$RkleinC\_\_{}_{}=RC1\times SC1{\_}_{}+RC2\times SC2{\_}_{}+RC3\times SC{3}_{}\text{\hspace{1em}( 16 )}$$

$$Rgroß{\_}_{}=RA\_\times S{A}_{}+RB\times S{B}_{}+RC\times S{C}_{}$$

Darunter sind RA1 die Einzelstück-Bestandskosten der großen Komponente A und SA1 _d die verbleibende Menge der großen Komponente A am Tag d. Andere Symbole sind gleich. RsmallA _d , RsmallB _d und RsmallC _d sind die Bestandskosten der kleinen Komponenten A, B und C am d-Tag, Rsmall die Bestandskosten der großen Komponente am d-Tag und R _d sind die gesamten Bestandskosten der Tag.
Die Summe sind die Bestandskosten am Tag d:

$$R_{}=RkleinA\_\_{}_{}+Rsmall{B}_{}+RkleinC\_\_{}_{}+Rgroß{\_}_{}+RW\_\times S{W}_{}\text{\hspace{1em}( 17 )}$$

5.1.9 Produktionsvorbereitungskosten

Wenn eine Fabrik ein Komponentenprodukt herstellt, muss sie Fixkosten zahlen, die unabhängig von der Produktionsmenge sind und als Produktionsvorbereitungskosten bezeichnet werden.Um die Berechnung der Fixkosten zu erleichtern, wird hier eine 0-1-Variable eingeführt. Nehmen wir als Beispiel die 0-1-Variable XW _d eines Produktionsroboters . Wenn am Tag d ein Roboter produziert wird, ist XW _d gleich 1; wenn am Tag d kein Roboter produziert wird, dann ist XW _d gleich 0. Folgendermaßen

$$X{W}_{}=\{\begin{array}{ll}1& MW{\_}_{}>0\\ & MW{\_}_{}=\end{array}\text{\hspace{1em}( 18 )}$$

Die 0-1-Variablen anderer Komponenten können auf die gleiche Weise erhalten werden.

Daher können gemäß den 0-1-Variablen aller Komponenten die Produktionsvorbereitungskosten von kleinen Komponenten, großen Komponenten und Robotern ausgedrückt werden.

$$FkleinerA\_\_{}_{}=XA1\_{\_}_{}\times FA1+XA{2}_{}\times FA2+XA3\_{\_}_{}\times FA3$$

$$FkleinesB\_\_{}_{}=XB1{\_}_{}\times FB1+XB{2}_{}\times FB2$$

$$FkleinerC\_\_{}_{}=XK{1}_{}\times FC1+XK{2}_{}\times FC2+XK{3}_{}\times FC3\text{\hspace{1em}( 19 )}$$

$$Fgroß{\_}_{}=FA\times XA{\_}_{}+FB\times XB{\_}_{}+FC\times XC{\_}_{}$$

Darunter ist XA1 _d die 0-1-Variable, ob Al am d-Tag produziert werden soll, und FA1 sind die Produktionsvorbereitungskosten von Al.
Andere Symbole sind gleich. FsmallA _d , FsmallB _d und FsmallC _d sind die Produktionsvorbereitungskosten der kleinen Komponenten A, B und C am d-Tag und die Bestandskosten der großen Fbig-Komponenten am d-Tag. F _d sind die Produktionsvorbereitungskosten am Tag d.

Die Summe sind die Produktionsvorbereitungskosten am Tag d:
$$F_{}=FkleinerA\_\_{}_{}+FkleinesB\_\_{}_{}+FkleinerC\_\_{}_{}+Fgroß{\_}_{}+X{W}_{}\times FW\_\text{\hspace{1em}( 20 )}$$

5.1.10 Zielfunktion

Die Gesamtkosten müssen am kleinsten sein, d. h. die Summe der Bestandskosten und der Produktionsvorbereitungskosten ist am kleinsten, und die Zielfunktion kann erhalten werden:

$$MinuteC=\sum _{d=1}{R}_{}+\sum _{d=1}{F}_{}\text{\hspace{1em}( 21 )}$$

5.2 Problemlösung des Modells

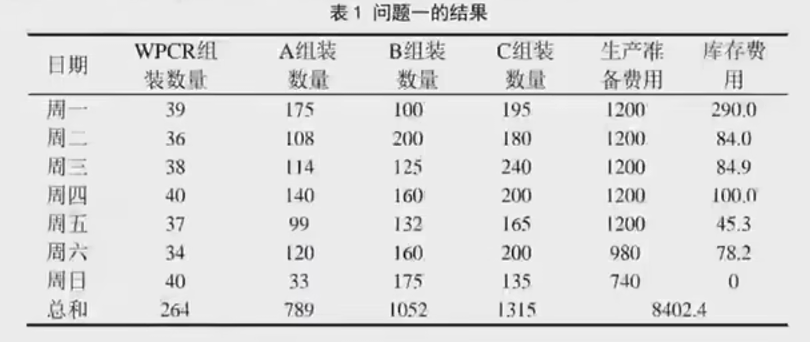
Der simulierte Abkühlungsalgorithmus wird mit dem Partikelschwarmalgorithmus kombiniert, und der Code wird in MATLAB geschrieben, um das Ergebnis von Problem eins zu erhalten, wie unten gezeigt.

Das Ergebnis hier ist etwas problematisch, es sollte 7000+ sein.

function [X,F]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C)
%初始化变量、计算目标函数值
flag1=0;
while flag1==0
X=[];
flag1=1;
KC_WPCR=zeros(1,length(WPCR));%记录每天WPCR库存
KC=zeros(3,length(WPCR));%记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));%记录每天交付WPCR情况
SY=zeros(3,length(WPCR));%记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));%记录每天组装WPCR情况
SC=zeros(3,length(WPCR));%记录每天生产ABC情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%第一天0库存
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的最小ABC需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
            flag2=1;
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=WPCR(i)-KC_WPCR(i-1);
        u=min(fix([x+KC(:,i-1)']./[A_x,B_x,C_x]));
    end
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i)=randi([s,u]);
    SC(:,i)=SC(:,i)+x';
    %放库存
    if i==1
        KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
        KC(:,i)=KC(:,i)+SC(:,i);
    else
        KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
        KC(:,i)=KC(:,i-1)+SC(:,i);
    end
    %使用
    SY_WPCR(i)=WPCR(i);
    SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);
    %更新库存
    KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
    KC(:,i)=KC(:,i)-SY(:,i);
end
X=[SC_WPCR;SC];
X=reshape(X',1,28);
end
X1=[SC_WPCR;SC];%生产
X2=[KC_WPCR;KC];%库存
X1(find(X1>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=sum(X1.*[W(1);sum(W(2:5));sum(W(6:8));sum(W(9:12))],2);
f2=sum(X2.*C([1,2,6,9])',2);
F=sum(f1)+sum(f2);"

function J=jianyan1(X,WPCR,A_x,B_x,C_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
KC_WPCR=zeros(1,length(WPCR));%记录每天WPCR库存
KC=zeros(3,length(WPCR));%记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));%记录每天交付WPCR情况
SY=zeros(3,length(WPCR));%记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));%记录每天组装WPCR情况
SC=zeros(3,length(WPCR));%记录每天生产ABC情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i)=X(i,1);
    SC(:,i)=SC(:,i)+x';
    %放库存
    if i==1
        KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
        KC(:,i)=KC(:,i)+SC(:,i);
    else
        KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
        KC(:,i)=KC(:,i-1)+SC(:,i);
    end
    %使用
    SY_WPCR(i)=WPCR(i);
    SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);
    %更新库存
    KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
    KC(:,i)=KC(:,i)-SY(:,i);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0
    J=1;
else
    J=0;
end 

function [F,f1,f2]=fun1(X,WPCR,A_x,B_x,C_x,W,C)
%带入变量计算目标函数值
X=reshape(X',7,4);
KC_WPCR=zeros(1,length(WPCR));%记录每天WPCR库存
KC=zeros(3,length(WPCR));%记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));%记录每天交付WPCR情况
SY=zeros(3,length(WPCR));%记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));%记录每天组装WPCR情况
SC=zeros(3,length(WPCR));%记录每天生产ABC情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i)=X(i,1);
    SC(:,i)=SC(:,i)+x';
    %放库存
    if i==1
        KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
        KC(:,i)=KC(:,i)+SC(:,i);
    else
        KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
        KC(:,i)=KC(:,i-1)+SC(:,i);
    end
    %使用
    SY_WPCR(i)=WPCR(i);
    SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);
    %更新库存
    KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
    KC(:,i)=KC(:,i)-SY(:,i);
end
X1=[SC_WPCR;SC];%生产
X2=[KC_WPCR;KC];%库存
X1(find(X1>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=sum(X1.*[W(1);sum(W(2:5));sum(W(6:8));sum(W(9:12))],1)';
f2=sum(X2.*C([1,2,6,9])',1)';
F=sum(f1)+sum(f2);

clear all
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
%每天总工时
T=[4500 2500 2750 2100 2500 2750 1500];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.95; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=1000; %颗粒总数，效果不好可以增加
X=[];
F=[];
for i=1:num
    [X(i,:),F(i,1)]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
 for i=1:num
        [XX(i,:),FF(i,1)]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan1(X,WPCR,A_x,B_x,C_x);
        if length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))>0 | sum(x(1,:))<sum(WPCR) | J==1
            XX(i,:)=X(i,:);
        end
        %计算目标函数
        FF(i,1)=fun1(X(i,:),WPCR,A_x,B_x,C_x,W,C);
        %更新最优
        if FF(i,1)<F(i,1)
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        end 
    end
    if min(F)<bestf
        [bestf,a]=min(F);
        bestx=X(a,:);
    end
    trace=[trace;bestf];
    T0=T0*alpha;
end
disp('最优解为：')
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量')
disp(reshape(bestx',7,4))
disp('生产准备费用、库存费用')
[~,f1,f2]=fun1(bestx,WPCR,A_x,B_x,C_x,W,C)
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')

6. Zusammenfassung und Lösung von Problem 2 Modell

6.1 Aufstellung des zweiten Problemmodells

6.1.1 Kleine Bauteile bauen große Bauteile zusammen

Die Komponenten A, B und C müssen einen Tag im Voraus produziert und eingelagert werden, um WPCR zusammenzubauen, und die Komponenten A1, A2, A3, B1, B2, C1, C2 und C3 müssen ebenfalls produziert und eingelagert werden einen Tag im Voraus, um A, B und C zusammenzubauen. Wenn Sie also den Bestellbedarf für Komponenten am Montag abschließen möchten, müssen Sie die großen Komponenten A, B und C zusammenbauen, die am Montag letzter Woche am Sonntag benötigt werden. Und am letzten Sonntag sollten die kleinen Komponenten, die zum Zusammenbau der großen Komponenten verwendet werden, am letzten Samstag zusammengebaut werden.
Daher sollte die Anzahl der kleinen Komponenten, die zum Zusammenbau großer Komponenten am Tag d verwendet werden, die Summe der Anzahl der kleinen Komponenten sein, die am Tag d-1 montiert wurden, und der Anzahl der kleinen Komponenten, die am Tag d-1 verbleiben. Daher werden die Formeln (5) und (6) modifiziert, um die Beschränkungen großer Komponenten wie folgt zu erhalten:
$$MA{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MA1\_{}_{d-}+SA1\_{}_{d-}}{6},\frac{MA2\_{}_{d-}+SA2\_{}_{d-}}{8},\frac{MA3\_{}_{d-}+SA3\_{}_{d-}}{2}\end{array}\right)\right]$$

$$MB{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MB1{\_}_{d-}+SB1{\_}_{d-}}{2},\frac{MB2{\_}_{d-}+SB2{\_}_{d-}}{4}\end{array}\right)\right]\text{\hspace{1em}( 22 )}$$

$$MC{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MC{1}_{d-}+SC1{\_}_{d-}}{8},\frac{MC{2}_{d-}+SC2{\_}_{d-}}{2},\frac{MC{3}_{d-}+SC3{\_}_{d-}}{12}\end{array}\right)\right]$$

6.1.2 Verbleibende Widgets

Die Anzahl der am Tag d verbleibenden Widgets, dh die Anzahl der Widgets, die gespeichert werden müssen, kann als zwei Teile betrachtet werden. Ein Teil ist die Anzahl der am Tag d montierten kleinen Komponenten, und der andere Teil ist der verbleibende Teil der am Tag d montierten großen Komponenten, und der verbleibende Teil sollte die Anzahl der am Tag d-1 montierten kleinen Komponenten und die Anzahl von sein verbleibende Kleinkomponenten am Tag d-1 und abzüglich der am Tag d verzehrten Menge,

Resttag d { am Tag d montierte Menge + (am Tag d montierte Menge − 1 + am Tag d − 1 verbleibende Menge) − am Tag d verbrauchte Menge verbleibend am Tag d\begin{cases} Tag d montierte Menge\\ +\ \ (Montagemenge am Tag d-1 + Restmenge am Tag d-1) - Verbrauchte Menge am Tag d\end{cases}Tag d bleibt⎩ ⎨ ⎧Am Tag d montierte Menge+( D−Menge in 1 Tag montiert+d_ _−1 Tag Restmenge)−Verbrauchte Menge Tag d

Der Rest des Widgets sieht also so aus:

$$SA{1}_{}=MA1\_{}_{}+MA1\_{}_{d-}+SA{1}_{d-}-6\times MA{\_}_{}$$
$$SA{2}_{}=MA2\_{}_{}+MA2\_{}_{d-}+SA{2}_{d-}-8\times MA{\_}_{}$$
$$SA{3}_{}=MA3\_{}_{}+MA3\_{}_{d-}+SA{3}_{d-}-2\times MA{\_}_{}$$
$$SB1{\_}_{}=MB1{\_}_{}+MB1{\_}_{d-}+SB1{\_}_{d-}-2\times MB{\_}_{}$$

$$SB2{\_}_{}=MB2{\_}_{}+MB2{\_}_{d-}+SB2{\_}_{d-}-4\times MB{\_}_{}\text{\hspace{1em}( 23 )}$$
$$SC1{\_}_{}=MC{1}_{}+MC{1}_{d-}+SC1{\_}_{d-}-8\times MC{\_}_{}$$
$$SC2{\_}_{}=MC{2}_{}+MC{2}_{d-}+SC2{\_}_{d-}-2\times MC{\_}_{}$$
$$SC{3}_{}=MC{3}_{}+MC{3}_{d-}+SC{3}_{d-}-12\times MC{\_}_{}$$

6.1.3 Die Bestückungsmenge des Roboters errechnet sich aus den verbleibenden Großbauteilen

Die Montage des Roboters ist die gleiche wie die Montage von kleinen Komponenten zu großen Komponenten. Am Tag d wird der Roboter unter Verwendung der Montage von Tag d-1 oder der verbleibenden großen Komponenten zusammengebaut. Die Einschränkungen sind wie folgt:

$$MW{\_}_{}⩽Mindest\left[\left(\begin{array}{c}\frac{MA1\_{}_{d-}+SA1\_{}_{d-}}{3},\frac{MB2{\_}_{d-}+SB2{\_}_{d-}}{4},\frac{MC{3}_{d-}+SC3{\_}_{d-}}{5}\end{array}\right)\right]\text{\hspace{1em}( 24 )}$$

Der Rest der großen Komponente ist wie folgt derselbe wie der Rest der kleinen Komponente:

$$S{A}_{}=MA{\_}_{}+MA{\_}_{d-}+S{A}_{d-}-3\times MW{\_}_{}$$
$$S{B}_{}=MB{\_}_{}+MB{\_}_{d-}+S{B}_{d-}-4\times MW{\_}_{}\text{\hspace{1em}( 25 )}$$
$$S{C}_{}=MC{\_}_{}+MC{\_}_{d-}+S{C}_{d-}-5\times MW{\_}_{}$$

6.1.4 Mengenbeschränkungen für die Robotermontage und Restberechnung

Die Montagemenge und der Rest des Roboters sind wie folgt unverändert:

$$MW{\_}_{}+S{W}_{d-}⩾D{W}_{}\text{\hspace{1em}( 26 )}$$
$$S{W}_{}=MC{\_}_{}+MW{\_}_{d-}+S{W}_{d-}-D{W}_{}\text{\hspace{1em}( 26 )}$$

6.1.5 Gewährleistung der Produktion am nächsten Tag

Um die Produktion am Montag nächster Woche zu gewährleisten, sollen die Komponenten am Ende dieser Woche am Sonntag stehen bleiben, also sind die Gleichungen (13) und (14) in Frage 1 nicht zu berücksichtigen. Betrachten Sie den nächsten Montag als den 8. Tag, daher sollte die Summe aus der Anzahl der am 8. Tag montierten Roboter und der verbleibenden Anzahl der Roboter am 7. Tag nicht weniger als die Bestellmenge 39 am nächsten Montag sein, wie folgt:

$$MW{\_}_{}+S{W}_{8-}⩾39\text{\hspace{1em}( 26 )}$$

Es ist erwähnenswert, dass in dieser Woche, um die Produktion von Robotern am Tag d sicherzustellen, die Beschränkungen für die Montagemenge großer Komponenten am Tag d und die Montagemenge kleiner Komponenten am Tag d-1 nicht eindeutig gegeben sind. Allerdings gibt es in Gleichung (26) eine Beschränkung der Auftragsmenge DW _d von Robotern am Tag d und der hergestellten Menge MW _{d am Tag d} . Es gibt eine Beschränkung der Montagemenge von großen Komponenten am Tag d, in Gleichung (22) gibt es eine Beschränkung der Montagemenge von kleinen Komponenten am Tag d-1 gegenüber der Anzahl von großen Komponenten, die am Tag d montiert werden.

Daher sind die Einschränkungen, um die Anzahl der am zweiten Tag produzierten Roboter zu garantieren, nicht ausdrücklich gegeben, aber implizit.

6.1.6 Arbeitszeitbeschränkungen

Die Arbeitszeitgrenze wird wie folgt nicht modifiziert:
$$3\times MA{\_}_{}+5\times MB{\_}_{}+5\times MC{\_}_{}⩽T_{}\text{\hspace{1em}( 27 )}$$

6.1.7 Zielfunktion

Die Zielfunktion wird nicht modifiziert und ist wie folgt dieselbe wie Problem 1:
$$MinuteC=\sum _{d=1}{R}_{}+\sum _{d=1}{F}_{}\text{\hspace{1em}( 28 )}$$

6.2 Die Lösung des zweiten Problemmodells

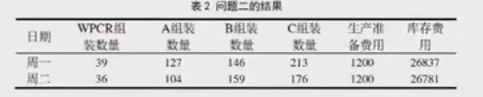
Verwenden Sie MATLAB, um den Code zu schreiben, um das Ergebnis der zweiten Frage zu erhalten.

clear
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];
%每天总工时
T=[4500 2500 2750 2100 2500 2750 1500];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.95; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=1000; %颗粒总数
X=[];
F=[];
for i=1:num
    [X(i,:),F(i,1)]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
 for i=1:num
        [XX(i,:),FF(i,1)]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan2(X,WPCR,A_x,B_x,C_x,D_x);
        if length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))>0 | sum(x(1,:))<sum(WPCR) | J==1
            XX(i,:)=X(i,:);
        end
        %计算目标函数
        FF(i,1)=fun2(X(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);
        %更新最优
        if FF(i,1)<F(i,1)
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
        end 
    end
    if min(F)<bestf
        [bestf,a]=min(F);
        bestx=X(a,:);
    end
    trace=[trace;bestf];
    T0=T0*alpha;
end
disp('最优解为：')
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量')
disp(reshape(bestx',7,4))
disp('生产准备费用、库存费用')
[~,f1,f2]=fun2(bestx,WPCR,A_x,B_x,C_x,W,C,D_x)
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')

function [X,F]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)
%初始化变量、计算目标函数值，小件提前两天，大件提前1天
flag1=0;
while flag1==0
X=[];
nn=2;%延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%假设第一天刚好满足WPCR
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的WPCR最小ABC需求量
        up=sub;
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
            flag2=1;
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=WPCR(i)-KC_WPCR(i+nn-1);
        u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
    end
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i+nn)=randi([s,u]);
    SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
    SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
    SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);
    if i==1
       KC_x(:,i+nn-2)=SC_x(:,i+nn-2);
    else
       KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
    end
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
    SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
    SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
    KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
X=[SC_WPCR(:,nn+1:end);SC(:,nn:end-1)];
X=reshape(X',1,28);
end
X1=[SC_WPCR(:,nn+1:end);SC(:,nn+1:end)];%生产
X2=[SC_x(:,nn+1:end)];%生产ABC小件
X3=[KC_WPCR(:,nn+1:end);KC(:,nn+1:end)];%库存ABC
X4=[KC_x(:,nn+1:end)];%库存ABC小件
X1(find(X1>0))=1;
X2(find(X2>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function [F,f1,f2]=fun2(X,WPCR,A_x,B_x,C_x,W,C,D_x)
%初始化变量、计算目标函数值
X=reshape(X',7,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i+nn)=X(i,1);
    SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
    SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
    SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);
    if i==1
       KC_x(:,i+nn-2)=SC_x(:,i+nn-2);
    else
       KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
    end
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
    SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
    SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
    KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
X1=[SC_WPCR(:,nn+1:end);SC(:,nn+1:end)];%生产
X2=[SC_x(:,nn+1:end)];%生产ABC小件
X3=[KC_WPCR(:,nn+1:end);KC(:,nn+1:end)];%库存ABC
X4=[KC_x(:,nn+1:end)];%库存ABC小件
X1(find(X1>0))=1;
X2(find(X2>0))=1;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function J=jianyan2(X,WPCR,A_x,B_x,C_x,D_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    SC_WPCR(i+nn)=X(i,1);
    SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
    SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
    SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);
    if i==1
       KC_x(:,i+nn-2)=SC_x(:,i+nn-2);
    else
       KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
    end
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
    SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
    SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
    KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0 | length(find(KC_x<0))>0
    J=1;
else
    J=0;
end

7. Erstellung und Lösung des Modells von Problem drei

7.1 Aufstellung des dritten Problemmodells

7.1.1 Bestimmung von Zeitvariablen

In dieser Frage hat sich die Zeit von 7 Tagen auf 30 Wochen und 210 Tage geändert, also ist die Zeitvariable
$$d\in (-1,0,1,...,208,209,210)\text{\hspace{1em}( 29 )}$$

d=-1 ist der Samstag der Vorwoche in Woche 1 und d=0 ist der Sonntag der Vorwoche in Woche 1. d=1 ist der Montag der 1. Woche, der der erste Tag der 30. Woche ist, d=210 ist der Sonntag der 30. Woche, der der letzte Tag der 30. Woche ist.

7.1.2 0-1 Variablen für Ausfallzeiten

Wenn bei der Modellierung das Problem auftritt, dass eine Variable mehrere ganzzahlige Werte annehmen kann, kann ein Satz von 0-1-Variablen verwendet werden, um die Variable zu ersetzen, indem die Eigenschaft ausgenutzt wird, dass eine 0-1-Variable eine binäre Variable ist. Daher wird aufgrund dieser Eigenschaft ein Satz von 0-1-Variablen eingeführt, um eine Ausfallzeit-0-1-Variable zu ersetzen.

Am Beispiel des ersten Wartungstermins stellt sich das Modell für den ersten Wartungstag wie folgt auf:

$$prüfen\_\_{\_}_{}=\{\begin{array}{ll}1& Tagiüberholt\; werden\\ & Keine\end{array}\text{\hspace{1em}( 29 )}$$

In der obigen Formel ist die erste Formel eine 0-1-Variable, was bedeutet, ob das erste Wartungsdatum der d-te Tag ist. Da der erste Wartungstag nur an einem der 210 Tage liegen kann, also nur ein Tag, wird die zweite obige Formel für Randbedingungen eingeführt.

Um den spezifischen Wert des Datums der ersten Wartung leicht zu erhalten, wird die dritte Formel in die obige Formel aufgrund der Eigenschaft eingeführt, dass die 0-1-Variable eine binäre Variable ist. Beispielsweise ist das Datum der 1. Überholung dann der 3. Tag

$${ich}_{}=1\text{\hspace{1em}( 31 )}$$
$${ich}_{}={ich}_{}={ich}_{}=...={ich}_{}={ich}_{1(210}=0\text{\hspace{1em}( 31 )}$$

Zu diesem Zeitpunkt ist die zweite Formel der Formel (30) erfüllt.
Dann kann die dritte Formel von (30) umgewandelt werden in:
$$prüfen\_\_{\_}_{}=2^1{ich}_{}+2^2{ich}_{}+...+2^{210}{ich}_{\left(1\right)}=2^1\times 0+2^2\times 0+2^3\times 1+...+2^{210}\times 0=2^3\text{\hspace{1em}( 31 )}$$

Durch die vierte Formel von (30) kann das Datum der ersten Inspektion wie folgt direkt erhalten werden:
$$Dateprüfen\_\_\_{}_{}=lo{g}_2^{prüfen}=lo{g}_2^{(2^3}=3\text{\hspace{1em}( 32 )}$$

Daher werden die 0–1-Variablen von 7 Inspektionen wie folgt erhalten:

wobei chechDate _t das spezifische Datum der t-ten Inspektion ist.

7.1.3 Inspektionsintervall

Um das Intervall von 6 Tagen zwischen zwei Inspektionsterminen bequemer anzugeben, wird die Reihenfolge von 7 Inspektionen zunächst eingeschränkt, d. h. das Prüfdatum _t wird zuerst sortiert, und zwar wie folgt:
$$ch\; echDatei<ch\; echDatei+1,ich\in (1,2,\mathrm{3...5},6)\text{\hspace{1em}( 34 )}$$

Nach der Sortierung gilt eine Sperrfrist von 6 Tagen zwischen zwei Prüfterminen wie folgt:

$$ch\; echDatei+6<ch\; echDatei+1,ich\in (1,2,\mathrm{3...5},6)\text{\hspace{1em}( 35 )}$$

7.1.4 Definition der Gesamtarbeitszeit-Grenzmatrix

Die Produktionszeit in dieser Frage hat sich von 7 Tagen auf 210 Tage in 30 Wochen geändert, also definieren Sie die Gesamtarbeitsstunden-Grenzmatrix neu:

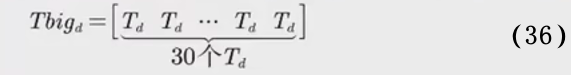
Darunter ist T _d die Gesamtarbeitsstundengrenze am d-Tag der Woche.

Daher sind die Beschränkungen, die die Gesamtmannstundengrenze erfüllen, wie folgt:

$$3\times MAd+5\times MBd+5\times MC{\_}_{}⩽Tsein{g}_{}\text{\hspace{1em}( 37 )}$$

7.1.5 Beschränkungen der Gesamtarbeitszeit werden nach der Wartung gelockert

Nach der Überholung der Anlage wurde die Produktionskapazität verbessert Nach dem ersten Tag nach der Überholung wird die Gesamtproduktionszeitbegrenzung um 10 %, 8 %, ..., 2 % und 0 % gelockert. Daher können, nachdem die konkreten Termine der 7 Inspektionen festgelegt sind, die Werte in der maximalen Gesamtarbeitsstunden-Grenzmatrix geändert werden, um die Lockerung nach der Inspektion zu erfüllen. Ändern Sie die Formel so, dass sie so aussieht:

$$Tsein{g}_{(chechDate+offset}=Tsein{g}_{(chechDate+offset}\times (1+(0.1-\mathrm{0,02}\times ausst\left)\right)\text{\hspace{1em}( 38 )}$$

$$ausst\_\in (0,1,...4,5)$$

Unter ihnen ist 1, Offset der Datumsoffset, der vom Datum jeder Wartung rückwärts versetzt wird, und die Limitlockerung wird für jeden Offset um 2 % reduziert. Wenn der Offset das 5-fache erreicht, wird die Grenzrelaxation auf 0 % reduziert und der Offset wird gestoppt.

7.1.6 Am Prüftag dürfen keine Bauteile produziert werden

Am Tag der Gerätewartung können keine Komponenten produziert werden, d. h. der Output von großen Komponenten, kleinen Komponenten und Robotern am Wartungstag ist 0, daher sind die Einschränkungen wie folgt:

$$MA1\_{}_{}=MA2\_{}_{}=MA3\_{}_{}=MB1{\_}_{}=MB2{\_}_{}=MC{1}_{}=MC{2}_{}=MC{3}_{}=0$$
$$MA{\_}_{}=MB{\_}_{}=MC{\_}_{}=MW{\_}_{}=0\text{\hspace{1em}( 39 )}$$
$$j\in (Dateprüfen\_\_\_{}_{},t\in (1,2,...6,7))$$

7.1.7 Sicherstellen, dass die Produktion fortgesetzt werden kann

Um sicherzustellen, dass nach Ablauf von 30 Wochen und 210 Tagen der Bestellbedarf noch am 31. Wochenmontag, also dem 211. Tag, erfüllt werden kann, also die Produktionsmenge MW des Roboters am 211. Tag und den Rest Die Menge SW11- des Roboters am 210. Tag sollte nicht kleiner sein als der 211. Tag DW.1, die Bedarfsmenge des Himmelsroboters, das Prinzip ist das gleiche wie das von 6.1.5. Die Einschränkungen sind wie folgt:

$$MW{\_}_{}+S{W}_{211-}⩾D{W}_{}\text{\hspace{1em}( 40 )}$$

Die Frage gibt nicht den Bedarf des Roboters am 211. Tag DW_{211} an, hier werden die 30-wöchigen Montagsdaten gemittelt und gerundet, um DW ₂₁₁ = 38 zu erhalten.

Andere Nebenbedingungen und Zielfunktionen wurden im Modell von Problem 2 nicht geändert, sodass sie hier nicht wiederholt werden.

7.2 Die Lösung des Drei-Modell-Problems

Verwenden Sie MATLAB, um Code zu schreiben, um das Ergebnis von Frage drei zu erhalten.

clear
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40
39 33 37 43 34 30 39
42 36 35 38 36 35 41
38 36 36 48 34 35 39
38 36 40 40 40 34 39
40 30 36 40 34 36 37
41 36 41 41 38 29 43
33 31 40 42 42 30 40
35 36 38 33 35 37 41
43 35 42 37 36 33 39
38 32 41 36 40 31 34
37 37 41 39 38 35 38
38 38 33 42 42 29 33
39 37 44 38 35 36 38
40 39 38 38 37 34 44
35 36 38 39 39 39 39
43 28 39 41 38 30 38
35 37 40 41 40 35 41
36 35 40 41 37 38 36
37 38 39 41 38 37 44
37 37 37 36 39 33 41
39 37 42 37 36 28 43
40 32 35 45 40 34 43
38 36 37 36 40 28 45
38 40 38 36 35 40 42
31 31 44 36 31 36 40
40 36 34 43 35 32 39
33 33 36 41 34 38 40
35 34 37 37 39 36 40
37 41 39 41 36 32 44];
WPCR=reshape(WPCR',210,1)';
WPCR=[WPCR,WPCR(1:2)];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];
%每天总工时
T=repmat([4500 2500 2750 2100 2500 2750 1500],1,30);
T=[T(end),T,T(1)];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.9; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=2; %颗粒总数
X=[];
A=[];
F=[];
for i=1:num
    [X(i,:),A(i,:),F(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
bestA=A(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
    AA=[];
 for i=1:num
        [XX(i,:),AA(i,:),FF(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
            A(i,:)=AA(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
                A(i,:)=AA(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        %粒子群算法限制最多找10次位置
        m=1;
        flag=0;
        while flag==1
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan3(x,AA(i,:),WPCR,A_x,B_x,C_x);
        if (length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))==0 & sum(x(1,:))>=sum(WPCR) & J==0) | m==10
            XX(i,:)=X(i,:);
        else
            m=m+1;
        end
        end
        %计算目标函数
        FF(i,1)=fun3(XX(i,:),AA(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);
        %更新最优
        if FF(i,1)<F(i,1)
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
            A(i,:)=AA(i,:);
        end 
    end
    if min(F)<bestf
        [bestf,a]=min(F);
        bestx=X(a,:);
        bestA=A(a,:);
    end
    trace=[trace;bestf];
    T0=T0*alpha;
end
disp('最优解为：')
disp('停检时间')
disp(bestA)
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量，见工作区矩阵zz')
x=reshape(bestx',212,4);
zz=[x(1:210,1),x(2:211,2:4)];
disp('生产准备费用、库存费用见工作区矩阵f1、f2')
[~,f1,f2]=fun3(bestx,bestA,WPCR,A_x,B_x,C_x,W,C,D_x);
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')

function [X,b,F]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)
%初始化变量、计算目标函数值，小件提前两天，大件提前1天
flag1=0;
while flag1==0
%检修
flag3=0;
while flag3==0
    A=zeros(1,length(WPCR));
    a=10+randperm(length(WPCR)-20);
    aa=a(1:7);
    A(aa)=1;
    b=find(A==1);
    c=b(2:end)-b(1:end-1);
    d=find(c<6);
    if length(d)==0
        flag3=1;
    end
end
%检修后提高效率
AA=[];%对应的时间
for i=1:length(b)
    AA=[AA,b(i)+1:b(i)+5];
end
G=repmat([1.1 1.08 1.06 10.4 1.02],1,length(b));
TT=T;
TT(AA)=TT(AA).*G;
X=[];
nn=2;%延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
% SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%假设第一天刚好满足WPCR
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的WPCR最小ABC需求量
        up=sub;
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])*2).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if i==1
            flag2=1;
        elseif i>1
            if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
                flag2=1;
            end
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=max(WPCR(i)-KC_WPCR(i+nn-1),0);
        u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
    end
    if u<s
        flag1=0;
        continue
    end
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=randi([s,u]);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X=[SC_WPCR(:,nn+1:end);SC(:,nn:end-1)];
X=reshape(X',1,848);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];%生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];%库存ABC
X4=[KC_x(:,nn+1:end-2)];%库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function [F,f1,f2]=fun3(X,b,WPCR,A_x,B_x,C_x,W,C,D_x)
%初始化变量、计算目标函数值
X=reshape(X',212,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
% SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=X(i,1);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];%生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];%库存ABC
X4=[KC_x(:,nn+1:end-2)];%库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function J=jianyan3(X,b,WPCR,A_x,B_x,C_x,D_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=X(i,1);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0 | length(find(KC_x<0))>0
    J=1;
else
    J=0;
end

8. Aufstellung und Lösung des Modells des vierten Problems

8.1 Die Einrichtung des Vier-Modells des Problems

8.1.1 Datenanalyse

Diese Frage muss die Nutzungsnachfrage von Robotern in der 31. Woche vorhersagen. Gemäß der durch die Frage gegebenen Datenanalyse hat die Datenschwankung eine gewisse Periodizität, und es handelt sich um Periodenzeitreihendaten. Es gibt nur eine abhängige Variable: die Anzahl der eingesetzten Roboter. Dann wird mit der Anzahl der verwendeten Roboter als abhängige Variable ein Vorhersagemodell für die Roboternachfrage basierend auf einer univariaten Zeitreihenanalyse erstellt.

Da die Daten mit Wochen als Zeitvariable keinen bestimmten Zeitraum angeben, sollten Sie die Daten in eine Trainingsgruppe und eine experimentelle Gruppe unterteilen, unterschiedliche Periodenlängen verwenden, um die Trainingsgruppe zu modellieren, die Modelle aussortieren, die den Q-Test bestehen, und Verwenden Sie dann die Daten der experimentellen Gruppe, um festzustellen, welches Modell die besten Vorhersagen macht. Wählen Sie das Modell mit dem kleinsten Vorhersagefehler aus, verwenden Sie alle Daten für die Neumodellierung und treffen Sie Vorhersagen für zukünftige Daten. Zeichnen Sie schließlich das vorhergesagte Zeitreihendiagramm, um zu beurteilen, ob der vorhergesagte Trend angemessen ist.

8.1.2 Datenvorverarbeitung

Beobachtungsdaten für 30 Wochen und 201 Tage ohne fehlende Daten. Definieren Sie eine Zeitvariable in Wochen, zeichnen Sie ein Zeitreihendiagramm mit der Zeit als horizontaler Achse und der Anzahl der Roboter als vertikale Achse. Analysieren Sie das Zeitreihendiagramm und stellen Sie fest, dass die Daten innerhalb eines bestimmten Bereichs ohne Trend oder Saisonalität nach oben und unten schwanken.

8.1.3 Erstellung eines Vorhersagemodells basierend auf univariaten Zeitreihen

Die Trainingsgruppendaten sind eine Sequenz mit einer Zykluslänge von 7, und das optimale Zeitreihenanalysemodell wird mithilfe des SPSS-Expertenmodellierers erstellt. Der Expert Modeler findet automatisch das am besten passende Modell für jede abhängige Sequenz. Wenn eine unabhängige (Prädiktor-)Variable angegeben wird, wählt der Modellierungsexperte für den Inhalt im ARIMA-Modell diejenigen Modelle aus, die einen statistisch signifikanten Zusammenhang mit der abhängigen Reihe haben. Modellvariablen wurden je nach Bedarf unter Verwendung von Differenz- oder Quadratwurzel- oder natürlichen Logarithmentransformationen transformiert. Standardmäßig berücksichtigt der Expert Modeler sowohl exponentielle Glättung als auch ARIMA-Modelle. Es ist jedoch auch möglich, den Expert Modeler darauf zu beschränken, nur nach ARIMA-Modellen oder nur nach exponentiellen Glättungsmodellen zu suchen. Sie können auch die automatische Erkennung von Ausreißern festlegen.

Der sPSS Expert Modeler hat automatisch das optimale Modell für uns ausgewählt: das einfache saisonale Modell.

8.1.4 Testen von Vorhersagemodellen

Überprüfen Sie, ob das Modell vollständig erkannt wird: Nach der Schätzung des Zeitreihenmodells müssen wir einen Test auf weißes Rauschen am Residuum durchführen. Wenn das Residuum weißes Rauschen ist, bedeutet dies, dass das von uns ausgewählte Modell das Gesetz der Zeitreihe vollständig identifizieren kann , das heißt, das Modell ist akzeptabel. ; Wenn das Residuum kein weißes Rauschen ist, bedeutet dies, dass es immer noch einige Informationen gibt, die vom Modell nicht erkannt werden, dann werden sie eliminiert.

Der ACF-Autokorrelationskoeffizient und die partielle PACF-Autokorrelationsfunktion können uns dabei helfen festzustellen, ob es sich bei dem Residuum um weißes Rauschen handelt, d. h. ob die Zeitreihe vom Modell vollständig erkannt werden kann.

Wie aus der obigen Tabelle ersichtlich ist, beträgt der durch den Q-Test für die Residuen erhaltene p-Wert 0,451, d. h. wir können die Nullhypothese nicht ablehnen und denken, dass die Residuen Sequenzen mit weißem Rauschen sind, also kann das einfache saisonale Modell dies gut tun Identifizieren Sie den Roboter in dieser Frage. Fordern Sie Daten an.

Modellvergleich und -auswahl: Verwenden Sie stationäre R ^2- oder AIC- und BIC-Kriterien. R ² kann verwendet werden, um die Qualität der linearen Modellanpassung widerzuspiegeln, je näher es an 1 liegt, desto genauer ist die Anpassung. Je mehr Parameter hinzugefügt werden, desto besser ist der Modellanpassungseffekt, aber dies geht zu Lasten der Komplexität des Modells (Overfitting-Problem). Daher sucht die Modellauswahl nach dem besten Gleichgewicht zwischen der Modellkomplexität und der Fähigkeit des Modells, die Daten zu interpretieren. Da BIC einen größeren Strafkoeffizienten für die Komplexität des Modells hat, ist BIC oft prägnanter als das von AIC ausgewählte Modell, daher das Prinzip, ein kleines R ² und BIC als Parameter für die Modellauswahl zu wählen.

Der BIC-Ausdruck (Bayesian Information Criterion) lautet wie folgt:

$$BichC=ln\left(T\right)(Anzahl\; der\; Parameter\; im\; Modell)-2ln(Maximum-Likelihood-Funktion\; des\; Modells)\text{\hspace{1em}( 41 )}$$

Holen Sie sich die vorhergesagten Werte für Woche 31: 38, 35, 39, 40, 37, 34, 40. Prognosewerte für die ersten beiden Tage der Woche 32: 38, 35. Rufen Sie daher die Bedarfsmengenmatrix des Roboters am d-ten Tag einer Woche in der Zukunft wie folgt ab:
$$DWPredict=[38,35,39,40,37,34,40,38,35]\text{\hspace{1em}( 42 )}$$

8.1.5 Jeden Tag eine normale Zustellung garantieren

Um sicherzustellen, dass die täglichen Roboterbestellungen mit einer Wahrscheinlichkeit von mehr als 95 % geliefert werden, werden die Beschränkungen für die Anzahl der montierten Roboter wie folgt geändert:

$$MW{\_}_{}+S{W}_{d-}⩾D{W}_{Predic{t}_{}}\times \mathrm{0,95}\text{\hspace{1em}( 43 )}$$

8.1.6 Gewährleistung einer normalen Lieferung während der Woche

Um sicherzustellen, dass Roboterbestellungen für die ganze Woche mit einer Wahrscheinlichkeit von mehr als 85 % ausgeliefert werden können, werden folgende Randbedingungen gemacht:

$$\sum _{d=1}MW{\_}_{}⩾\mathrm{0,85}\times \sum _{d=1}DWPredic{t}_{}\text{\hspace{1em}( 44 )}$$
Es ist erwähnenswert, dass die täglichen Bestellungen mit einer Wahrscheinlichkeit von mehr als 95 % geliefert wurden und die Roboterbestellungen der ganzen Woche mit einer Wahrscheinlichkeit von mehr als 85 % geliefert werden müssen, d. h. Gleichung (44) wurde in Gleichung (43) impliziert. Daher reicht es aus, jeden Tag eine normale Lieferung sicherzustellen, dh Formel (43) kann ignoriert werden.

Neun, die offizielle Standardantwort

1. Das Endergebnis der ersten Frage

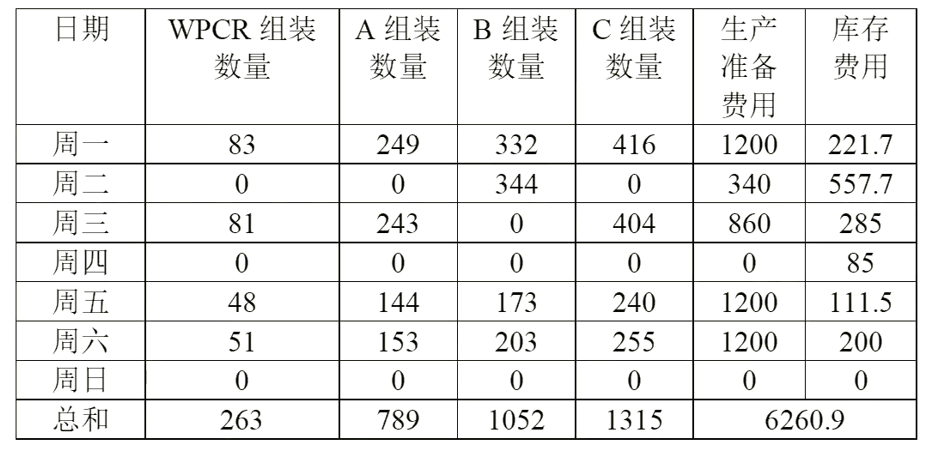
2. Das Endergebnis der zweiten Frage

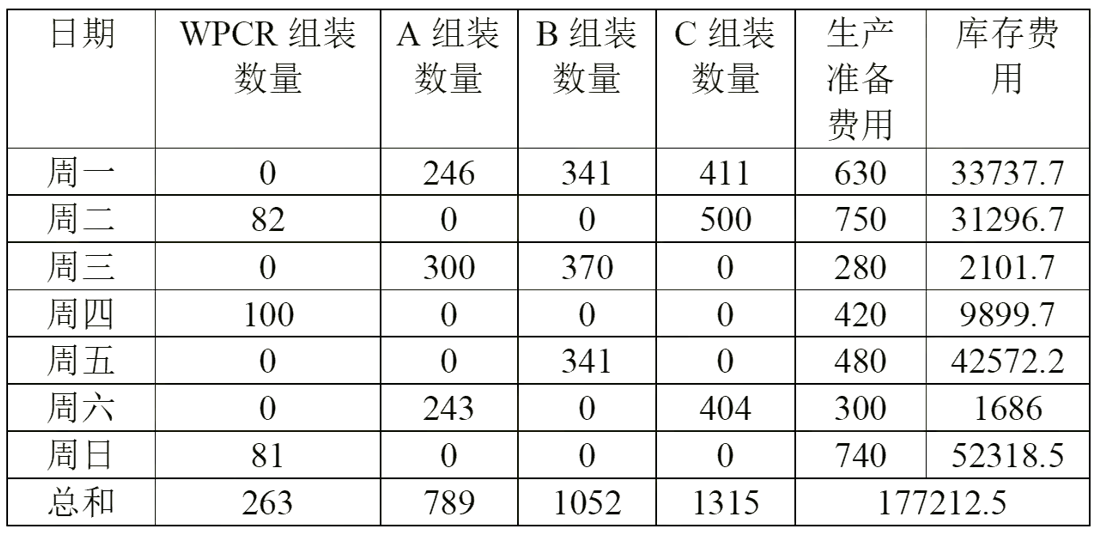
3. Das Endergebnis der dritten Frage

4. Das Endergebnis der vierten Frage