Harbin Institute of Technology 2022 Machine Learning Experiment 1: Curve Fitting

Die Anforderungen dieses Experiments sind (im Vergleich zum vorherigen Semester) recht klar. Dieser Blog ist in Python implementiert, die Scientific Computing Library wird verwendet numpy, und die Zeichnung wird verwendet matplotlib.pyplot. Importieren Sie der Einfachheit halber Folgendes am Anfang der Datei:

import numpy as np
import matplotlib.pyplot as plt

Die in diesem Experiment verwendeten numpy-Funktionen

Allgemein numpyabgekürzt als np(import numpy as np). Das Folgende ist eine kurze Einführung in die im Experiment verwendeten numpy-Funktionen. Der folgende Code muss oben hinzugefügt werden import numpy as np.

np.array

Diese Funktion gibt ein numpy.ndarrayObjekt zurück, das als mehrdimensionales Array verstanden werden kann (in diesem Experiment werden nur eindimensionale (kann als Spaltenvektor angesehen werden) und zweidimensionale (Matrix) verwendet). Verwenden Sie den Kleinbuchstaben $xx$ ist ein Spaltenvektor, Großbuchstabe$A$ repräsentiert eine Matrix. A.TbedeutetAATransponieren von$A.$Die Operationen an Paarenndarraysind im Allgemeinen elementweise.

>>> x = np.array([1,2,3])
>>> x
array([1, 2, 3])
>>> A = np.array([[2,3,4],[5,6,7]])
>>> A
array([[2, 3, 4],
       [5, 6, 7]])
>>> A.T # 转置
array([[2, 5],
       [3, 6],
       [4, 7]])
>>> A + 1
array([[3, 4, 5],
       [6, 7, 8]])
>>> A * 2
array([[ 4,  6,  8],
       [10, 12, 14]])

np.zufällig

np.randomDas Modul enthält mehrere Funktionen zur Generierung von Zufallszahlen. In diesem Experiment werden zufällige Initialisierungsparameter (Gradientenabstiegsverfahren) verwendet, um den Daten Rauschen hinzuzufügen.

>>> np.random.rand(3, 3) # 生成3 * 3 随机矩阵，每个元素服从[0,1)均匀分布
array([[8.18713933e-01, 5.46592778e-01, 1.36380542e-01],
       [9.85514865e-01, 7.07323389e-01, 2.51858374e-04],
       [3.14683662e-01, 4.74980699e-02, 4.39658301e-01]])
      
>>> np.random.rand(1) # 生成单个随机数
array([0.70944563])
>>> np.random.rand(5) # 长为5的一维随机数组
array([0.03911319, 0.67572368, 0.98884287, 0.12501456, 0.39870096])
>>> np.random.randn(3, 3) # 同上，但每个元素服从N(0, 1)（标准正态）

mathematische Funktion

Nur in diesem Experiment verwendet np.sin. Diese mathematischen Funktionen np.ndarrayarbeiten elementweise:

>>> x = np.array([0, 3.1415, 3.1415 / 2]) # 0, pi, pi / 2
>>> np.round(np.sin(x)) # 先求sin再四舍五入: 0, 0, 1
array([0., 0., 1.])

Darüber hinaus gibt es np.logFunktionen np.exp, die der Bibliothek von Python ähneln math(nur für elementweise Operationen auf mehrdimensionalen Arrays).

np.dot

Gibt das Produkt zweier Matrizen zurück. Stimmt mit der Matrixmultiplikation in der linearen Algebra überein. Die Spalten der ersten Matrix müssen gleich der Anzahl der Zeilen der zweiten Matrix sein. Insbesondere wenn eines davon ein eindimensionales Array ist, wird die Form automatisch an $n\times 1$ oder$1\times n.$

>>> x = np.array([1,2,3]) # 一维数组
>>> A = np.array([[1,1,1],[2,2,2],[3,3,3]]) # 3 * 3矩阵
>>> np.dot(x,A)
array([14, 14, 14])
>>> np.dot(A,x)
array([ 6, 12, 18])

>>> x_2D = np.array([[1,2,3]]) # 这是一个二维数组（1 * 3矩阵）
>>> np.dot(x_2D, A) # 可以运算
array([[14, 14, 14]])
>>> np.dot(A, x_2D) # 行列不匹配
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<__array_function__ internals>", line 5, in dot
ValueError: shapes (3,3) and (1,3) not aligned: 3 (dim 1) != 1 (dim 0)

np.auge

np.eye(n)Gibt eine Einheitsmatrix der Ordnung n zurück.

>>> A = np.eye(3)
>>> A
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Lineare Algebra-Korrelation

np.linalgist eine Bibliothek zur linearen Algebra.

>>> A
array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])
>>> np.linalg.inv(A) # 求逆（本实验不考虑逆不存在）
array([[1.        , 0.        , 0.        ],
       [0.        , 0.5       , 0.        ],
       [0.        , 0.        , 0.33333333]])
>>> x = np.array([1,2,3])
>>> np.linalg.norm(x) # 返回向量x的模长（平方求和开根号）
3.7416573867739413
>>> np.linalg.eigvals(A) # A的特征值
array([1., 2., 3.])

Daten generieren

Das Erzeugen der Daten erfordert das Hinzufügen von Rauschen (Fehler). Das im Unterricht gegebene Beispiel ist die Sinusfunktion, wir verwenden auch die Standard-Sinusfunktion $Y=\mathrm{Sünde}x.$ (Nach dem Hinzufügen von Rauschen ist es$Y=\mathrm{Sünde}x+ϵ,$ mit$ϵ\sim N(0,p^2)$, da$\mathrm{Sünde}$Der Maximalwert von$x$$1$ setzen wir die Varianz des Fehlers kleiner, hier auf$\frac{}{25}$).

'''
返回数据集，形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1], 默认为(0, 10)
'''
def get_dataset(N = 100, bound = (0, 10)):
    l, r = bound
    # np.random.rand 产生[0, 1)的均匀分布，再根据l, r缩放平移
    # 这里sort是为了画图时不会乱，可以去掉sorted试一试
    x = sorted(np.random.rand(N) * (r - l) + l)
	
	# np.random.randn 产生N(0,1)，除以5会变为N(0, 1 / 25)
    y = np.sin(x) + np.random.randn(N) / 5
    return np.array([x,y]).T

Der resultierende Datensatz hat einen Punkt auf einer Ebene pro Zeile. Die resultierenden Daten sehen so aus:

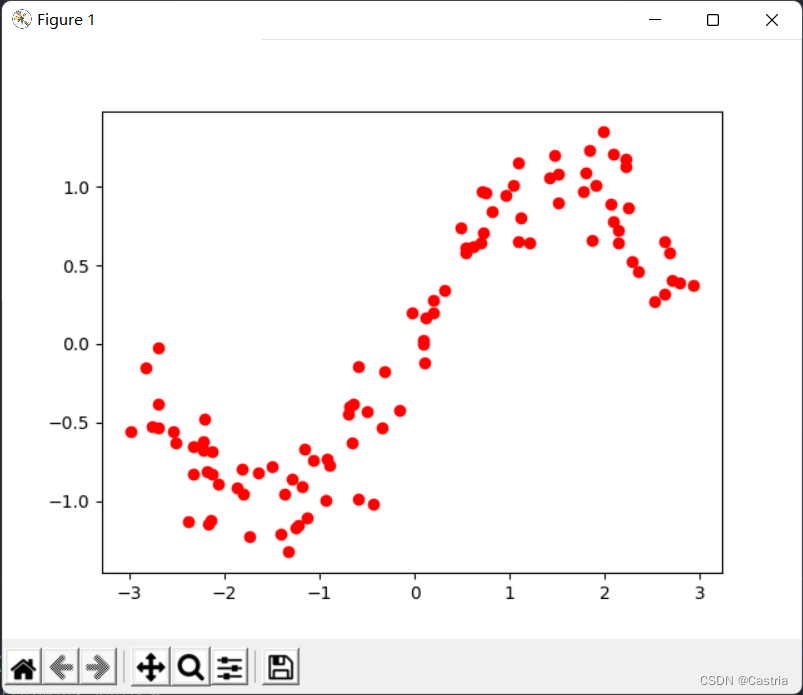
vage in Form einer Sinusfunktion. Der Code, der das obige Bild erzeugt, lautet wie folgt:

dataset = get_dataset(bound = (-3, 3))
# 绘制数据集散点图
for [x, y] in dataset:
    plt.scatter(x, y, color = 'red')
plt.show()

Kleinste-Quadrate-Anpassung

Unten verwenden wir vier Methoden (kleinste Quadrate, reguläre Term-/Kammregression, Gradientenabstieg, konjugierter Gradient), um die obigen gestörten Sinuskurven mit Polynomen anzupassen.

Analytische Lösungsableitung

Erinnern Sie sich einfach an das Prinzip der Methode der kleinsten Quadrate: Jetzt wollen wir ein mm verwendenPolynom$f\; (\; x\; )\; vom\; Grad\; m$
$$f\left(x\right)={in}_{}+{in}_{}x+{in}_{}{x}^2+...+{in}_{}{x}^m$$
zur Annäherung an die wahre Funktion$Y=\mathrm{Sünde}x.$ Unser Ziel ist es, die Datensätze$(x_{},Y_{}),(x_{},Y_{}),...,(x_{},Y_{})$ auf den Verlust$L$ (Verlust), wobei die Verlustfunktion den quadrierten Fehler nimmt:
$$L=\sum _{ich=1}[{und}_{}-f(x_{}){]}^2$$
Um die Parameter${in}_{},{in}_{},...,{in}_{},$ müssen wir den Verlust$L$ bezogen auf w 0 , w 1 , . . . , wm w_0, w_1,...,w_m${in}_{},{in}_{},...,{in}_{}$Ableitung von . Der Einfachheit halber verwenden wir die Notation der linearen Algebra:
$$X={⎝\begin{array}{ccccc}1& x_{}& x_1^{}& \cdots & x_1^{}\\ 1& x_{}& x_2^{}& \cdots & x_2^{}\\ ⋮& & & & ⋮\\ & x_{}& x_N^{}& & x_N^{}\end{array}⎠}_{N\times (m+1},Y={⎝\begin{array}{c}{Y}_{}\\ Y_{}\\ ⋮\\ Y_{}\end{array}⎠}_{N\times },Im={⎝\begin{array}{c}{in}_{}\\ {in}_{}\\ ⋮\\ {in}_{}\end{array}⎠}_{(m+1)\times }.$$
Unter dieser Darstellung ist
$$⎝\begin{array}{c}f\left(x_{}\right)\\ f\left(x_{}\right)\\ ⋮\\ f(x_{}\end{array}⎠=XW.$$
Wenn Sie irgendwelche Zweifel haben, können Sie es selbst mit der Matrixmultiplikation überprüfen$$.$$Fortfahrend kann die Summe der Fehlerterme ausgedrückt werden als
$$⎝\begin{array}{c}f\left(x_{}\right)-Y_{}\\ f\left(x_{}\right)-Y_{}\\ ⋮\\ f\left(x_{}\right)-Y_{}\end{array}⎠=XW-Y.\; Daherist$$
die Verlustfunktion
$$L=(XW\_-und{)}^T(XW-Y).$$
(Um den Vektor$xx=(x_{},x_{},...,x_{}{)}^{}$Die Summe der Quadrate der Komponenten von${}^T$$xx$ ist das Skalarprodukt, also${xx}^{T}xx.$ )
zur Erlangung des$L$ kleinste$W$ (dieses$W$ ein Spaltenvektor ist), müssenwirFinde die partielle Ableitung von$L$$0:$
$$\begin{array}{rl}\frac{\partial L}{\partial W}& =\frac{}{\partial W}[(XW-und{)}^T(XW-J)]\\ & =\frac{}{\partial W}[(W^{TX}{\_}^T-Y^T\left)\right(XW-J)]\\ & =\frac{}{\partial W}({W.}^{TX}{\_}^{T}XW-{Im}^{TX}{\_}^{TY}\_-Y^{T}XW+Y^{TY})\_\\ & =\frac{}{\partial W}({W.}^{TX}{\_}^{T}XW-2J^{T}XW+Y^{T}Y)(leicht\; zu\; überprüfen,{Im}^{TX}{\_}^{TY}\_=Y^{T}XW,somit\; kombinierbar)\\ & =2X{\_}^{T}XW-2X{\_}^{TY}\end{array}$$
Beschreibung:
(1) Von Zeile 3 bis Zeile 4 aufgrund von ${Im}^{TX}{\_}^{T}Y$和$Y^{T}XW$sind alles Zahlen (oder$1\times 1$ -Matrix), die beiden sind gegeneinander transponiert, sodass die Werte gleich sind und zu einem Element kombiniert werden können.
(2) Ableitung der Matrix von Zeile 4 nach Zeile 5, erster Term$\frac{}{\partial W}\left({W.}^T\right(X^{T}X\left)W\right)$handelt von$Die\; quadratische\; Form\; von\; W$ , ihre Ableitung ist$2X{\_}^{T}XW.($
3) Für den primären Term$-2J^{Die\; Ableitung\; von\; T}XW$, wenn die Ableitung nach dem reellen Zahlenfeld erfolgt, sollte$-2J^{T}X.überprüfen$Sie und stellen Sie fest, dass der Typ der Matrix nicht korrekt ist, Sie müssen eine Transposition durchführen, es wird$-2X{\_}^{TY}.\_$

Matrix-lineare Algebra wurde im Unterricht nicht systematisch gelehrt, nur um zu erklären, was hier erscheint. ( Ich werde nicht, wenn es mehr gibt )
Lassen Sie die partielle Ableitung 0 sein, erhalten
$$X^{T}XW=Y^{T}X,$$
links multiplizieren$(X^{T}X{)}^{-1}$（$X^{}$Siehe den ergänzenden Hinweis unten für die Umkehrbarkeit von${}^T$$X$
$$Im=(X^{T}X{)}^{-1X}{\_}^{T}Y.$$
Das ist der$$WW$$$Für\; die\; analytische\; Lösung\; von\; W$ müssen wir nur die Funktion aufrufen, um diesen Wert zu berechnen.

'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''
def fit(dataset, m = 5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)

Erklären Sie den Code ein wenig: Die erste Zeile erzeugt das oben vereinbarte $Die\; X$ -Matrix,dataset[:,0]die die 0. Spalte des Datensatzes ist$(x_{},x_{},...,x_{}{)}^T$ ; die zweite Zeile ist$Y$ -Matrix; die dritte Zeile gibt die obige analytische Lösung zurück. (Wenn Sie mit Python-Syntax oder -Bibliotheken nicht vertraut sindnumpy, ist dies ziemlich unfreundlich.)

Verifizieren Sie einfach das Ergebnis der von uns ausgeführten Funktion: Dazu schreiben wir zunächst eine drawFunktion zur Konvertierung des erhaltenen WWDas Polynomf ( x ) f(x)$entsprechend\; W$Zeichnen Sie$f$$($$x$$)$pyplot auf das Bibliotheksbild:

'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''
def draw(dataset, w, color = 'red', label = ''):
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = np.dot(X, w)
    
    plt.plot(dataset[:, 0], Y, c = color, label = label)

Dann die Hauptfunktion:

if __name__ == '__main__':
    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    # 最小二乘
    coef1 = fit(dataset)
    draw(dataset, coef1, color = 'black', label = 'OLS')
    
	# 绘制图像
    plt.legend()
    plt.show()

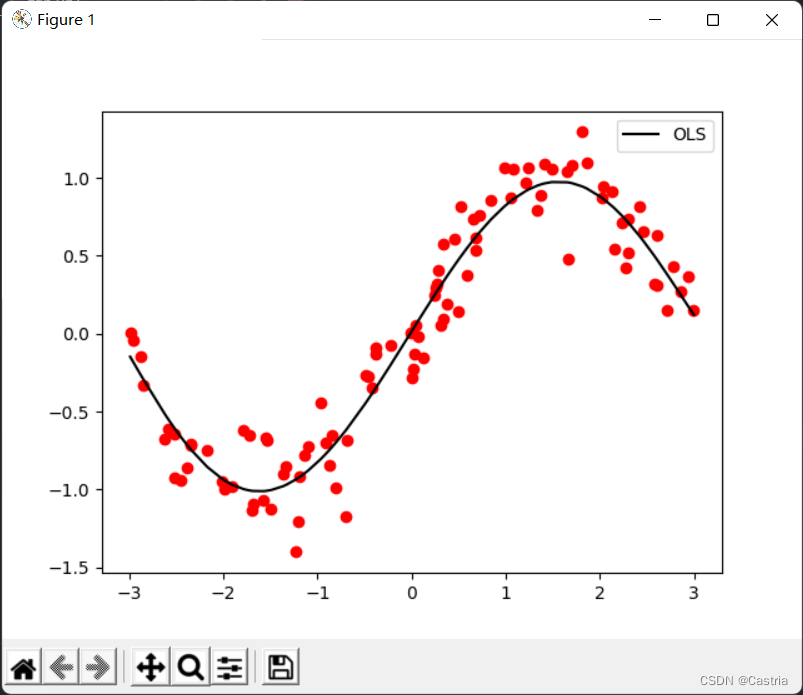
Es ist ersichtlich, dass der Effekt der Polynomanpassung 5. Grades ziemlich gut ist (der Datensatz wird jedes Mal zufällig generiert, unterscheidet sich also vom ersten Bild).

Wie beim gesamten Code in diesem Teil werden die folgenden gleichnamigen Funktionen nicht mehr beschrieben:

import numpy as np
import matplotlib.pyplot as plt

'''
返回数据集，形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1]
'''
def get_dataset(N = 100, bound = (0, 10)):
    l, r = bound
    x = sorted(np.random.rand(N) * (r - l) + l)
    y = np.sin(x) + np.random.randn(N) / 5
    return np.array([x,y]).T

'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''
def fit(dataset, m = 5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)
'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''
def draw(dataset, w, color = 'red', label = ''):
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = np.dot(X, w)
    
    plt.plot(dataset[:, 0], Y, c = color, label = label)

if __name__ == '__main__':

    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    
    coef1 = fit(dataset)
    draw(dataset, coef1, color = 'black', label = 'OLS')

    plt.legend()
    plt.show()

Ergänzende Anweisungen

Oben gibt es ein weniger strenges Stück: für eine Matrix $Für\; X$ ,$X^{T}X$ist nicht unbedingt reversibel. In diesem Experiment kann jedoch gezeigt werden, dass es sich um eine invertierbare Matrix handelt. Da diese Klasse keine lineare Algebra-Klasse ist, werden wir nicht zu viel Platz darauf verwenden, nur eine kurze Erinnerung:
(1)$X$ ist ein$N\times (M+1)$ der Matrix. wobei die Anzahl der Daten$N$ ist viel größer als der Polynomgrad$m$ , es gibt$N>m+1;$
(2) Zur Veranschaulichung$X^{T}X$ist invertierbar, muss erklärt werden$(X^{T}X{)}_{(m+1)\times (m+1}$Voller Rang, das heißt $R\left(X^{T}X\right)=m+1;$
(3) In der linearen Algebra haben wir bewiesen, dass$R\left(X\right)=R\left(X^T\right)=R\left(X^{T}X\right)=R\left(XX{\_}^T\right);$
(4)$X$ ist eineVandermonde-Matrix,deren Rang gleich$mein\{N,m+1\}=m+1.$

Regularisierungsterm hinzufügen (ridge regression)

Die Methode der kleinsten Quadrate ist anfällig für Überanpassung. Um diesen Fehler zu veranschaulichen, verwenden wir die ersten 50 Punkte des generierten Datensatzes zum Training (damit die Abtastung nicht gleichmäßig genug ist, hier nur zur Veranschaulichung der Überanpassung), erhalten die Parameter und zeichnen dann das gesamte Funktionsbild um die Anpassungswirkung zu überprüfen:

if __name__ == '__main__':
    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    # 取前50个点进行训练
    coef1 = fit(dataset[:50], m = 3)
    # 再画出整个数据集上的图像
    draw(dataset, coef1, color = 'black', label = 'OLS')

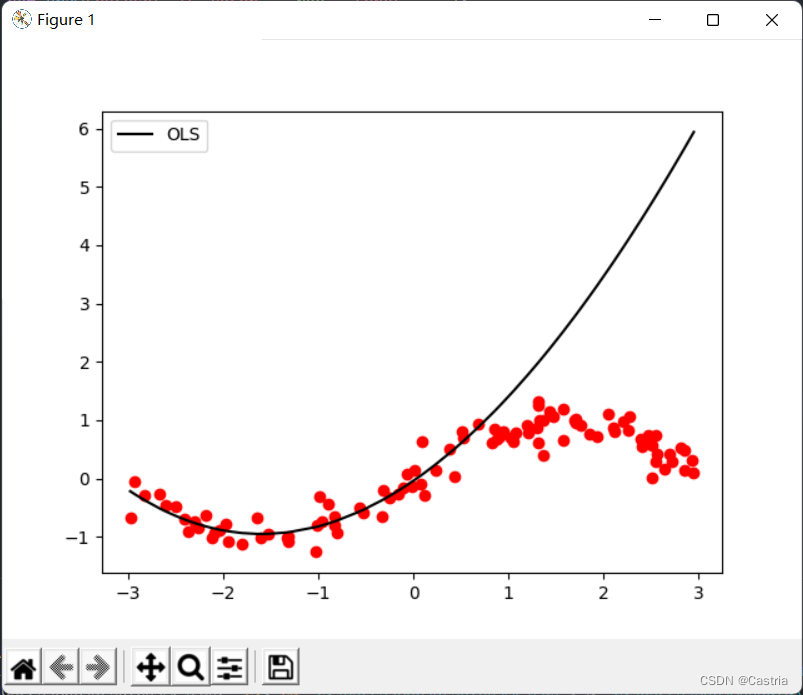
Überanpassung in mmDies ist besonders gravierend, wenn$m$$m=3$ Uhr). Wenn der Polynomgrad zunimmt, um dem gegebenen Datensatz so nahe wie möglich zu kommen, wird die Größe der berechneten Koeffizienten größer und größer, und die Leistung bei unsichtbaren Proben wird schlechter. Wie oben gezeigt, können Sie sehen, dass die Anpassung an den ersten 50 Punkten liegt (ungefähr auf der Abszisse$[-3,0]$ ) ist sehr gut, auf dem Testset ist die Performance sehr schlecht ($[0,3]$ ). Um eine Überanpassung zu verhindern, kann ein Regularisierungsterm eingeführt werden. Zu diesem Zeitpunkt ist die Verlustfunktion$L$变为
$$L=(XW\_-und{)}^T(XW-und)+\lambda ||W|{|}_2^{}$$
wobei $||\cdot |{|}_2^{}$Zeigt $L_{}$Das Quadrat der Norm, in diesem Fall ${Im}^{T}W;\lambda$ ist der Regularisierungskoeffizient. Diese Formel wird auch als Ridge-Regression bezeichnet. Seine Idee ist es, die Verlustfunktion und den resultierenden Parameter WWzu berücksichtigen$Modulo-Länge\; von\; W$ (bei$L_{}$Norm), verhindert $Der\; Parameter\; in\; W$ ist zu groß.

Zum Beispiel (Zahlen werden zufällig zusammengesetzt): wenn der Regularisierungskoeffizient $1$ , wenn der quadratische Fehler von Schema 1 auf dem Datensatz$\mathrm{0,5},$ zu diesem Zeitpunkt$Im=(100,-200,300,150{)}^T$ ; der quadratische Fehler von Schema 2 auf dem Datensatz ist$10,$ zu diesem Zeitpunkt$Im=(1,-3,2,1)$ , dann wählen wir$W.Regularisierungskoeffizient$ λ$\lambda$ charakterisiert dies für$Die\; Bedeutung\; der\; W$ -Modullänge:λ \lambdaJe größer$\lambda$$Je\; höher\; die\; Modullänge\; von\; W$ , desto größer die Strafe. Wenn$l=0wird\; die$ Ridge-Regression zur gewöhnlichen Methode der kleinsten Quadrate. Ähnlich wie bei der Ridge-Regression ist LASSO, das den Regularisierungsterm durch$L_{}$Norm.

Durch Wiederholung der obigen Ableitung erhalten wir die analytische Lösung als
$$Im=(X^{TX}\_+\lambda E{\_}_{m+}{)}^{-1X}{\_}^{T}Y.wobei$$E m + 1 E_{m+1
}${UND}_{m+}$ist $m+Einheitenmatrix\; 1.$ Ordnung. Man erhält leicht$(X^{TX}\_+\lambda E{\_}_{m+})$ ist ebenfalls reversibel.

Dieser Teil des Codes lautet wie folgt.

'''
岭回归求解析解, m 为多项式次数, l 为 lambda 即正则项系数
岭回归误差为 (XW - Y)^T*(XW - Y) + λ(W^T)*W
- dataset 数据集
- m 多项式次数, 默认为 5
- l 正则化参数 lambda, 默认为 0.5
'''
def ridge_regression(dataset, m = 5, l = 0.5):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    Y = dataset[:, 1]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X) + l * np.eye(m + 1)), X.T), Y)

Der Vergleich der beiden Methoden sieht wie folgt aus:

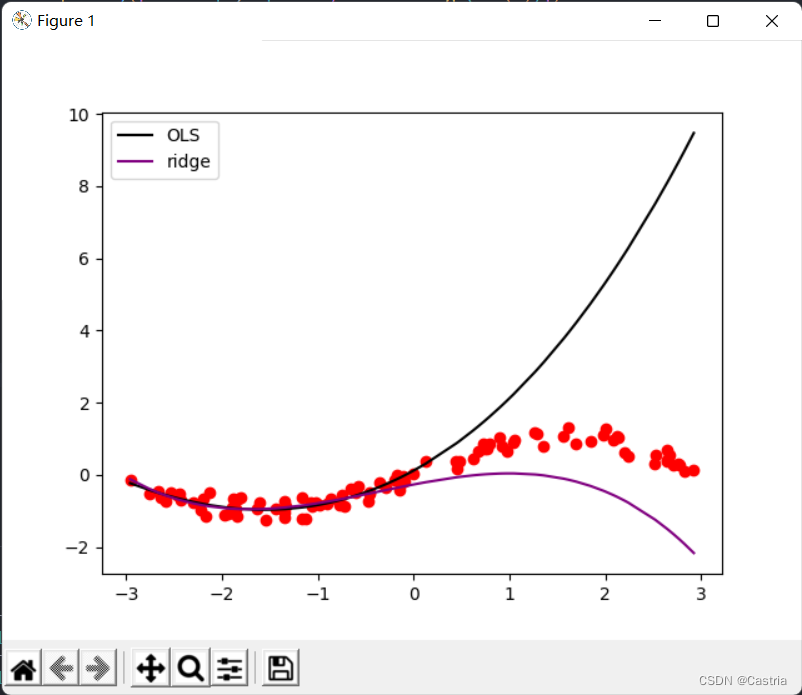
Aus dem Vergleich ist ersichtlich, dass die Ridge-Regression das Overfitting deutlich reduziert (zu diesem Zeitpunkt $m=3,l=\mathrm{0,3}$ ).

Gradientenabstieg

Der Gradientenabstieg ist nicht der beste Weg, um dieses Problem zu lösen, und es kann leicht dazu führen, dass er nicht konvergiert. Stellen Sie zunächst kurz die Grundidee der Gradientenabstiegsmethode vor: Wenn wir die komplexe Funktion f ( x ) f(x) finden wollenDer Minimalwert (Maximalpunkt) von$f$$($$x$$)$$x$ kann ein Vektor sein usw.),
$$x_{}=\underset{x}{\mathrm{Arg}}f\left(x\right)$$
Gradientenabstieg wiederholt die folgenden Operationen:
(0) (zufällig)$x_{}(t=0)$ ;
(1) Sei$f\left(x\right)$ in$x_{}$Steigung bei (wenn $Wenn\; x$ eindimensional ist, ist es die Ableitung)$\nabla f\left(x_{}\right)$；
（2）$x_{t+}=x_{}-\eta \nabla f\left(x_{}\right)$
(3) Wenn$x_{t+}$mit $x_{}$Wenn es wenig Unterschied gibt (erreicht den voreingestellten Bereich) oder die Anzahl der Iterationen die voreingestellte Obergrenze erreicht, stoppen Sie den Algorithmus; andernfalls wiederholen Sie (1) (2).

Darunter η \ eta$\eta$ ist die Lernrate, die die Schrittgröße des Gradientenabstiegs bestimmt.
Das Folgende ist eine Gradientenabstiegsmethode, um$Y=x^{}$Beispielprogramm für den Minimalpunkt${}^{2\; :}$

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return x ** 2

def draw():
    x = np.linspace(-3, 3)
    y = f(x)
    plt.plot(x, y, c = 'red')

cnt = 0
# 初始化 x
x = np.random.rand(1) * 3
learning_rate = 0.05

while True:
    grad = 2 * x
    # -----------作图用，非算法部分-----------
    plt.scatter(x, f(x), c = 'black')
    plt.text(x + 0.3, f(x) + 0.3, str(cnt))
    # -------------------------------------
    new_x = x - grad * learning_rate
    # 判断收敛
    if abs(new_x - x) < 1e-3:
        break

    x = new_x
    cnt += 1

draw()
plt.show()

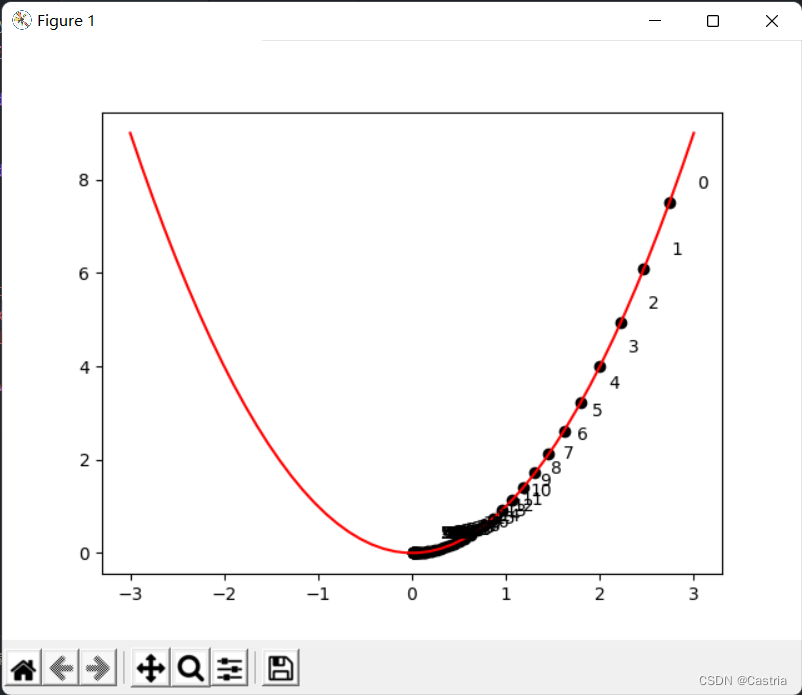
Das obige Bild zeigt $x$ Während sich die Iteration entwickelt, können Sie$x$ nähert sich entlang der positiven Halbachse immer weiter Null. Es ist zu beachten, dass die Lernrate nicht zu groß sein darf (obwohl im obigen Programm die Lernrate etwas klein eingestellt ist), sie muss manuell angepasst werden, sonst ist es leicht vorstellbar,$x$ oszilliert auf der positiven und negativen Halbachse hin und her, was eine Konvergenz erschwert.

Bei der Methode der kleinsten Quadrate ist die zu optimierende Funktion die Verlustfunktion
$$L=(XW\_-und{)}^T(XW-Y)$$
Als nächstes lösen wir das Problem mit dem Gradientenabstieg$$.$$In der obigen Herleitung gilt
$$\begin{array}{r}\frac{\partial L}{\partial W}=2X{\_}^{T}XW-2X{\_}^{TY}\end{array},$$
also jedes Mal, wenn wir eine Iteration auf$W$ subtrahiert diesen Gradienten bis zum Parameter$W$ konvergiert. Nach Experimenten wird der quadratische Fehler jedoch den Gradienten zu groß machen und der Prozess kann nicht konvergieren.Daher wird der mittlere quadratische Fehler (MSE) verwendet, um ihn zu ersetzen, was darin besteht, die ursprüngliche Formel durch$N$ :

'''
梯度下降法(Gradient Descent, GD)求优化解, m 为多项式次数, max_iteration 为最大迭代次数, lr 为学习率
注: 此时拟合次数不宜太高(m <= 3), 且数据集的数据范围不能太大(这里设置为(-3, 3)), 否则很难收敛
- dataset 数据集
- m 多项式次数, 默认为 3(太高会溢出, 无法收敛)
- max_iteration 最大迭代次数, 默认为 1000
- lr 梯度下降的学习率, 默认为 0.01
'''
def GD(dataset, m = 3, max_iteration = 1000, lr = 0.01):
    # 初始化参数
    w = np.random.rand(m + 1)

    N = len(dataset)
    X = np.array([dataset[:, 0] ** i for i in range(len(w))]).T
    Y = dataset[:, 1]

    try:
        for i in range(max_iteration):
            pred_Y = np.dot(X, w)
            # 均方误差（省略系数2）
            grad = np.dot(X.T, pred_Y - Y) / N
            w -= lr * grad
    '''
    为了能捕获这个溢出的 Warning，需要import warnings并在主程序中加上：
    warnings.simplefilter('error')
    '''
    except RuntimeWarning:
        print('梯度下降法溢出, 无法收敛')

    return w

Zu diesem Zeitpunkt, wenn $Wenn\; m$ etwas größer eingestellt ist (z. B. 4), läuft der Gradient während der Iteration über, sodass die Parameter nicht konvergieren können. Beim Konvergieren ist der Anpassungseffekt in Ordnung:

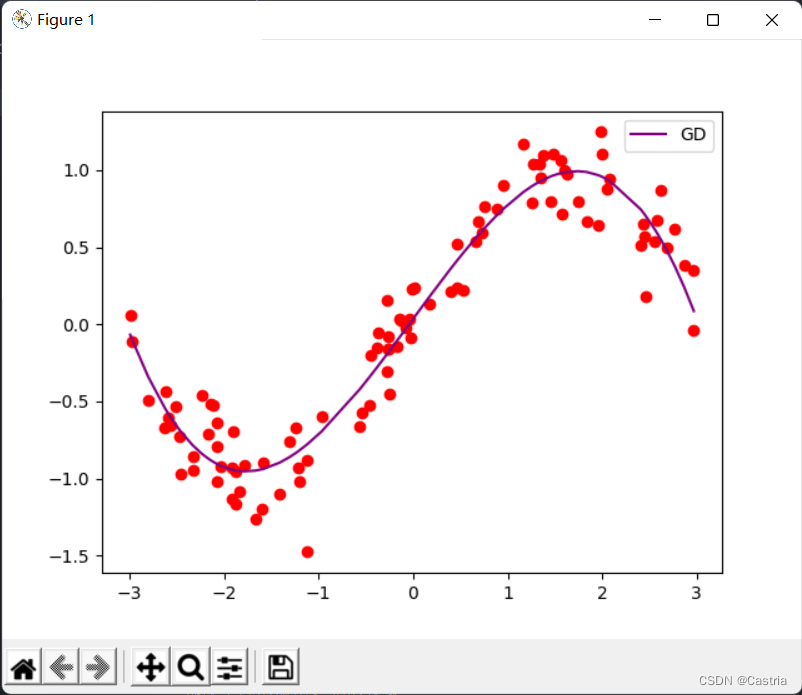
Konjugierte Gradientenmethode

Konjugierte Gradienten können verwendet werden, um die Form $EINxx=b$Gleichungssystem für$b$$f\left(xx\right)=\frac{}{2}{xx}^{TA}\_xx-{bb}^{T}xx+c.$ (Es kann gezeigt werden, dass für positiv definite$A$ , die beiden sind äquivalent) wobei$A$ ist einepositiv definiteMatrix. In diesem Problem fragen wir nach der Lösung von$$X^{T}XW=Y^{T}X,$$
dann${EIN}_{(m+1)\times (m+1}=X^{T}X,bb=Y^{T.}Wenn\; wir\; einen\; regulären\; Term\; hinzufügen$wollen, wird daraus die Lösung
$$(X^{TX}\_+\lambda E)W=Y^{T}X.$$
Lassen Sie mich zunächst erklären:$$XTXX$$$X^{T}X$ist nicht unbedingt positiv definit, muss aber positiv semidefinit sein (siehe). Aber im Experiment brauchen wir uns um dieses Problem im Grunde nicht zu kümmern, denn$X^{T}X$ist sehr wahrscheinlich positiv definit, wir fügen dem Code nur eine Behauptung hinzu und schenken dieser Bedingung nicht viel Aufmerksamkeit.
Die Idee der Methode der konjugierten Gradienten und der Beweisprozess sind relativ lang. Sie können aufdiese Serie. Hier werden nur die Algorithmusschritte angegeben (am Anfang des dritten oben verlinkten Artikels):

(0) x initialisieren $x_{(0};$
(1) Initialisiere$d_{(0}=r_{(0}=b-Ein{x}_{(0};$
（2）令$$a_{(ich}=\frac{r_{\left(ich\right)}^{}{r}_{(ich}}{d_{\left(ich\right)}^{}Ein{d}_{(ich}};$$
（3）迭代$x_{(ich+1}=x_{(ich}+a_{(ich}{d}_{(ich};$
（4）令$r_{(ich+1}=r_{(ich}-a_{(ich}Ein{d}_{(ich};$
（5）令$$b_{(ich+1}=\frac{r_{(ich+1)}^{}{r}_{(ich+1}}{r_{\left(ich\right)}^{}{r}_{(ich}},d_{(ich+1}=r_{(ich+1}+b_{(ich+1}{d}_{(ich}.$$
（6）当$\frac{||r{\_}_{(ich}}{||r{\_}_{(0}||}<ϵ$ , stoppe den Algorithmus, andernfalls iteriere weiter ab (2). $ϵ$ ist ein kleiner voreingestellter Wert, ich nehme hier$10^{-5.}$
Im Folgenden folgen wir diesem Prozess, um den Code$zu$

'''
共轭梯度法(Conjugate Gradients, CG)求优化解, m 为多项式次数
- dataset 数据集
- m 多项式次数, 默认为 5
- regularize 正则化参数, 若为 0 则不进行正则化
'''
def CG(dataset, m = 5, regularize = 0):
    X = np.array([dataset[:, 0] ** i for i in range(m + 1)]).T
    A = np.dot(X.T, X) + regularize * np.eye(m + 1)
    assert np.all(np.linalg.eigvals(A) > 0), '矩阵不满足正定!'
    b = np.dot(X.T, dataset[:, 1])
    w = np.random.rand(m + 1)
    epsilon = 1e-5

    # 初始化参数
    d = r = b - np.dot(A, w)
    r0 = r
    while True:
        alpha = np.dot(r.T, r) / np.dot(np.dot(d, A), d)
        w += alpha * d
        new_r = r - alpha * np.dot(A, d)
        beta = np.dot(new_r.T, new_r) / np.dot(r.T, r)
        d = beta * d + new_r
        r = new_r
        # 基本收敛，停止迭代
        if np.linalg.norm(r) / np.linalg.norm(r0) < epsilon:
            break
    return w

Verglichen mit dem naiven Gradientenabstiegsverfahren konvergiert das konjugierte Gradientenverfahren schnell und stabil. Mit zunehmendem Grad des Polynoms wird die Anpassung jedoch schlechter: bei $m=7$ wird es wie folgt mit der Methode der kleinsten Quadrate verglichen:

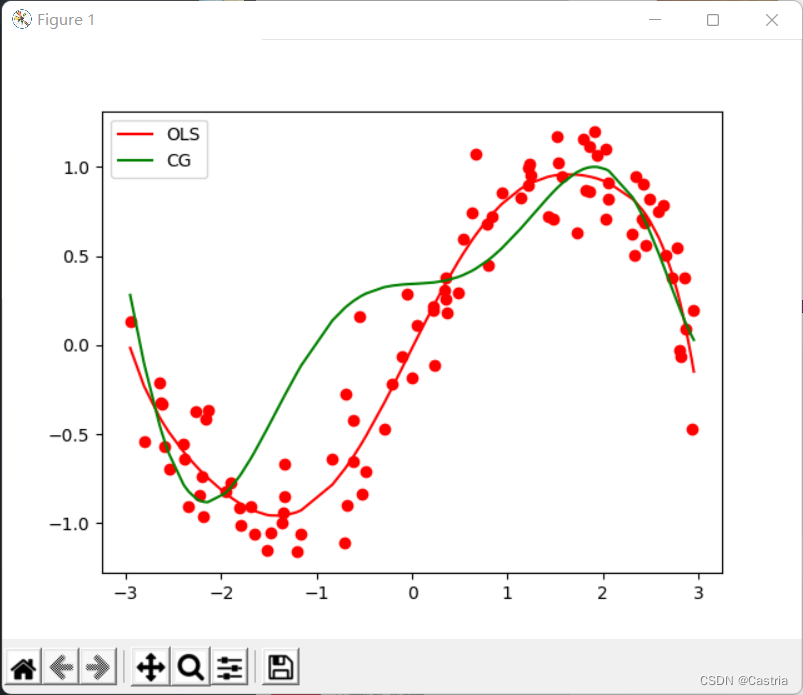
Zu diesem Zeitpunkt kann es noch teilweise durch den regulären Term gemildert werden (die Zahl ist$m=7,l=1$ ):

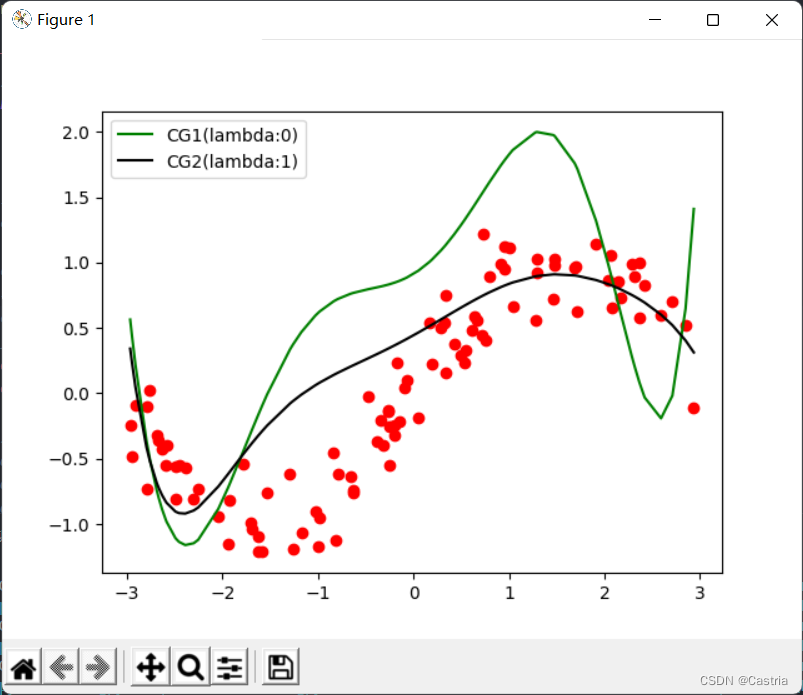
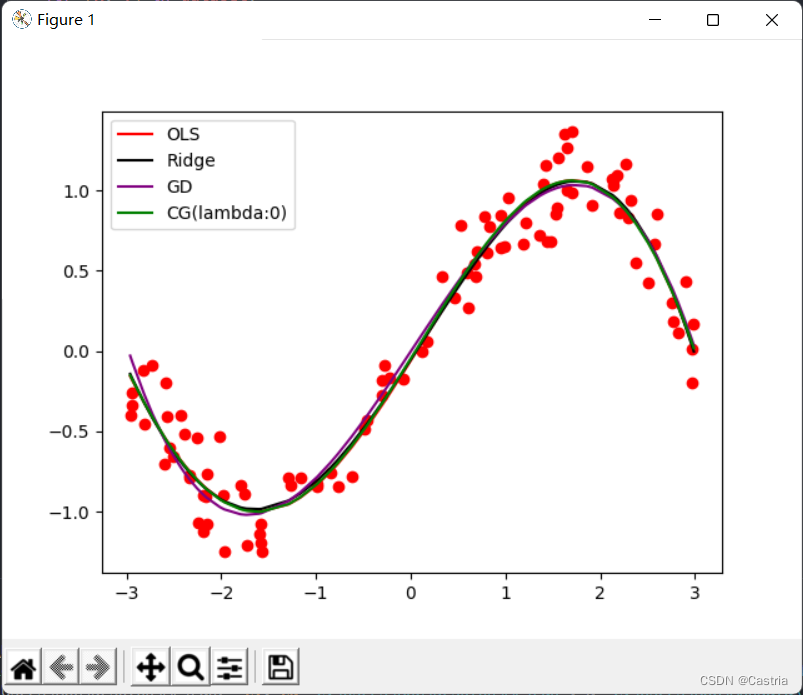
Schließlich sind die passenden Bilder der vier Methoden (im Grunde gleich) und der Hauptfunktion beigefügt, und die Parameter können entsprechend den experimentellen Anforderungen angepasst werden:

if __name__ == '__main__':
    warnings.simplefilter('error')

    dataset = get_dataset(bound = (-3, 3))
    # 绘制数据集散点图
    for [x, y] in dataset:
        plt.scatter(x, y, color = 'red')
    
    
    # 最小二乘法
    coef1 = fit(dataset)
    # 岭回归
    coef2 = ridge_regression(dataset)
    # 梯度下降法
    coef3 = GD(dataset, m = 3)
    # 共轭梯度法
    coef4 = CG(dataset)
    
    # 绘制出四种方法的曲线
    draw(dataset, coef1, color = 'red', label = 'OLS')
    draw(dataset, coef2, color = 'black', label = 'Ridge')
    draw(dataset, coef3, color = 'purple', label = 'GD')
    draw(dataset, coef4, color = 'green', label = 'CG(lambda:0)')

    # 绘制标签, 显示图像
    plt.legend()
    plt.show()