Erfahren Sie, wie Transformers "denken"

Mobile 2023-03-28 20:35:34 views: null

Transformer-Modelle sind die Grundlage von KI-Systemen. Es gibt bereits unzählige Diagramme der Kernstruktur, "wie Transformer funktioniert".

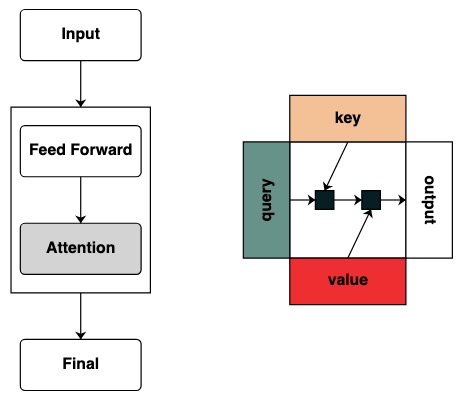
Diese Diagramme bieten jedoch keine intuitive Darstellung des Rahmens zum Berechnen dieses Modells. Wenn ein Forscher daran interessiert ist, wie ein Transformer funktioniert, ist es sehr nützlich, eine Intuition darüber zu haben, wie er funktioniert.

In dem Paper Thinking Like Transformers wird ein Rechengerüst der Transformer-Klasse vorgeschlagen, das Transformer-Berechnungen direkt berechnet und imitiert. Mit der Programmiersprache RASP wird jedes Programm in einen speziellen Transformer kompiliert.

In diesem Blogbeitrag habe ich eine Variante von RASP (RASPy) in Python nachgebildet. Die Sprache ist ungefähr die gleiche wie im Original, aber mit ein paar weiteren Änderungen, die ich für interessant halte. Mit diesen Sprachen bietet die Arbeit der Autorin Gail Weiss eine herausfordernde Reihe interessanter und korrekter Möglichkeiten, um zu verstehen, wie sie funktionieren.

!pip install git+https://github.com/srush/RASPy

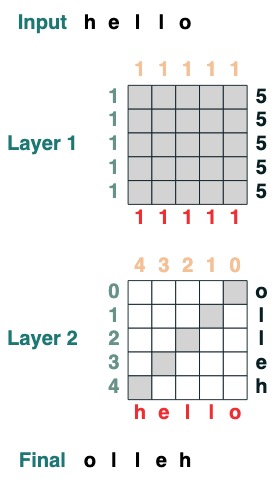
Bevor wir über die Sprache selbst sprechen, sehen wir uns ein Beispiel an, wie das Codieren mit Transformers aussieht. Hier ist ein Code, der einen Flip berechnet, dh die Eingabesequenz umkehrt. Der Code selbst verwendet zwei Transformer-Schichten, um Aufmerksamkeit und mathematische Berechnungen anzuwenden, um zu diesem Ergebnis zu gelangen.

def flip():
    length = (key(1) == query(1)).value(1)
    flip = (key(length - indices - 1) == query(indices)).value(tokens)
    return flip
flip()

Artikelverzeichnis

  • Teil 1: Transformatoren als Code
  • Teil II: Programme mit Transformern schreiben

Transformatoren als Code

Unser Ziel ist es, eine Reihe von Berechnungsformen zu definieren, die die Darstellung von Transformatoren minimieren. Wir werden jedes Sprachkonstrukt und sein Gegenstück in Transformers durch Analogie beschreiben. (Für die offizielle Sprachspezifikation siehe den Link zum vollständigen Text des Papiers am Ende dieses Artikels).

Die Kerneinheit der Sprache ist die Sequenzoperation, die eine Sequenz in eine andere Sequenz gleicher Länge umwandelt. Ich werde sie später Transformationen nennen.

eingeben

In einem Transformer ist die Basisschicht eine Feedforward-Eingabe für ein Modell. Diese Eingabe enthält normalerweise unformatierte Token- und Standortinformationen.

Im Code stellen die Merkmale von Token die einfachste Transformation dar, die die Token nach dem Modell zurückgibt, und die Standardeingabesequenz ist "hello":

tokens

Wenn wir die Eingabe in der Transformation ändern möchten, verwenden wir die Eingabemethode, um den Wert zu übergeben.

tokens.input([5, 2, 4, 5, 2, 2])

Als Transformer können wir die Positionen dieser Sequenzen nicht direkt akzeptieren. Aber um Standorteinbettungen zu simulieren, können wir den Index des Standorts erhalten:

indices


sop = indices
sop.input("goodbye")

Feedforward-Netzwerk

Nachdem wir die Eingabeschicht passiert haben, erreichen wir die Feedforward-Netzwerkschicht. In Transformer wendet dieser Schritt mathematische Operationen unabhängig auf jedes Element der Sequenz an.

Im Code stellen wir diesen Schritt dar, indem wir Transformationen berechnen. An jedem Element der Sequenz werden unabhängige mathematische Operationen durchgeführt.

tokens == "l"

Das Ergebnis ist eine neue Transformation, die als umgestaltet berechnet wird, sobald die neue Eingabe rekonstruiert ist:

model = tokens * 2 - 1
model.input([1, 2, 3, 5, 2])

Diese Operation kann mehrere Transforms kombinieren. Nehmen Sie zum Beispiel die oben genannten Token und Indizes als Beispiel, hier können Sie Transformer klassifizieren, um mehrere Informationen zu verfolgen:

model = tokens - 5 + indices
model.input([1, 2, 3, 5, 2])


(tokens == "l") | (indices == 1)

Wir stellen einige Hilfsfunktionen bereit, um das Schreiben von Transformationen zu vereinfachen, beispielsweise whereum eine Struktur mit ähnlicher ifFunktionalität .

where((tokens == "h") | (tokens == "l"), tokens, "q")

mapErmöglicht es uns, unsere eigenen Operationen zu definieren, z. B. intdas Konvertieren . (Benutzer sollten vorsichtig mit Operationen sein, die von einfachen neuronalen Netzwerken berechnet werden, die verwendet werden können.)

atoi = tokens.map(lambda x: ord(x) - ord('0'))
atoi.input("31234")

Funktionen (Funktionen) können die Kaskade dieser Transformationen leicht beschreiben. Die folgende Operation ist beispielsweise die Operation, bei der und atoi angewendet und 2 hinzugefügt wird

def atoi(seq=tokens):
    return seq.map(lambda x: ord(x) - ord('0')) 

op = (atoi(where(tokens == "-", "0", tokens)) + 2)
op.input("02-13")

Aufmerksamkeitsfilter

Die Dinge beginnen interessant zu werden, wenn Sie anfangen, den Aufmerksamkeitsmechanismus anzuwenden. Dies ermöglicht den Austausch von Informationen zwischen den verschiedenen Elementen der Sequenz.

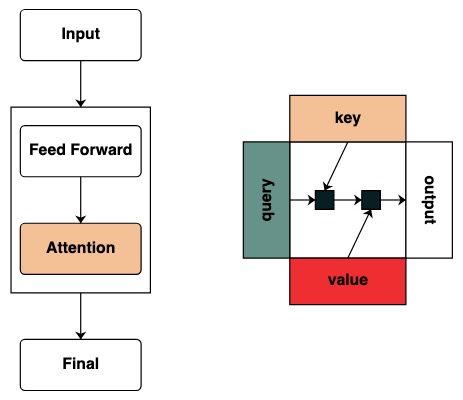
Wir beginnen damit, das Konzept von Schlüssel und Abfrage zu definieren. Schlüssel und Abfragen können direkt aus den obigen Transformationen erstellt werden. Wenn wir zum Beispiel einen Schlüssel definieren wollen, nennen wir ihn key.

key(tokens)

querygleich für

query(tokens)

Skalare keykönnen queryals oder verwendet werden und senden die Länge der zugrunde liegenden Sequenz.

query(1)

Wir erstellen Filter, um Operationen zwischen Schlüssel und Abfrage anzuwenden. Dies entspricht einer binären Matrix, die angibt, um welchen Schlüssel es sich bei jeder Abfrage handelt. Im Gegensatz zu Transformers werden dieser Aufmerksamkeitsmatrix keine Gewichtungen hinzugefügt.

eq = (key(tokens) == query(tokens))
eq

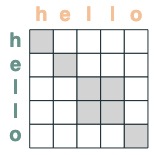
Einige Beispiele:

  • Die Übereinstimmungsposition des Selektors wird um 1 versetzt:
offset = (key(indices) == query(indices - 1))
offset

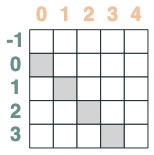
  • Ein Selektor, dessen Schlüssel vor der Abfrage liegt:
before = key(indices) < query(indices)
before

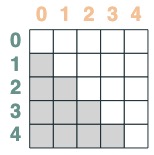
  • Ein Selektor, dessen Schlüssel später als die Abfrage ist:
after = key(indices) > query(indices)
after

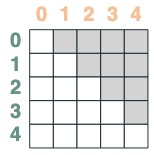
Selektoren können über boolesche Operationen kombiniert werden. Dieser Selektor kombiniert beispielsweise before und eq, und wir zeigen dies, indem wir ein Schlüssel-Wert-Paar in die Matrix aufnehmen.

before & eq

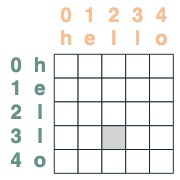
Aufmerksamkeitsmechanismus nutzen

Bei einem Aufmerksamkeitsselektor können wir eine Folge von Werten für die Aggregation bereitstellen. Wir aggregieren, indem wir die von diesen Selektoren ausgewählten Wahrheitswerte akkumulieren.

(Hinweis: In der Originalarbeit verwenden sie eine durchschnittliche Aggregationsoperation und zeigen eine clevere Struktur, in der die durchschnittliche Aggregation die Summenberechnung darstellen kann. RASPy verwendet standardmäßig die Akkumulation, um es einfach zu halten und eine Fragmentierung zu vermeiden. Tatsächlich bedeutet dies, dass dies kratzig ist kann die Anzahl der benötigten Schichten unterschätzen. Durchschnittsbasierte Modelle benötigen möglicherweise die doppelte Anzahl an Schichten)

Beachten Sie, dass Aggregationsoperationen es uns ermöglichen, Features wie Histogramme zu berechnen.

(key(tokens) == query(tokens)).value(1)

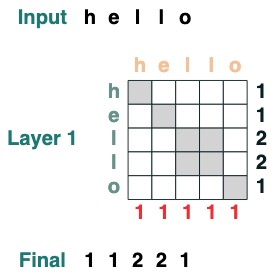
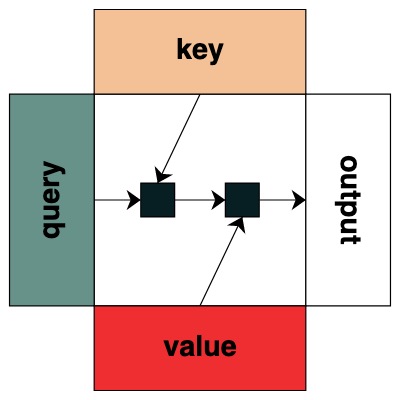
Visuell folgen wir der Diagrammstruktur mit Abfrage links, Schlüssel oben, Wert unten und Ausgabe rechts

Einige Vorgänge des Aufmerksamkeitsmechanismus erfordern nicht einmal ein Eingabetoken. Um beispielsweise die Sequenzlänge zu berechnen, erstellen wir einen Aufmerksamkeitsfilter „alle auswählen“ und weisen ihm einen Wert zu.

length = (key(1) == query(1)).value(1)
length = length.name("length")
length

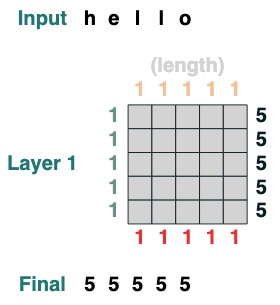
Hier sind komplexere Beispiele, die unten Schritt für Schritt gezeigt werden. (Es ist wie ein Interview)

Wir wollen die Summe benachbarter Werte einer Folge berechnen, zuerst kürzen wir vorwärts:

WINDOW=3
s1 = (key(indices) >= query(indices - WINDOW + 1))  
s1

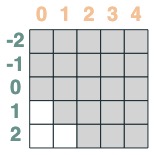
Dann kürzen wir rückwärts:

s2 = (key(indices) <= query(indices))
s2

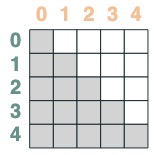
Beide schneiden sich:

sel = s1 & s2
sel

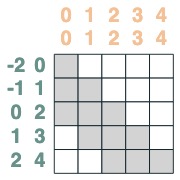
Endgültige Aggregation:

sum2 = sel.value(tokens) 
sum2.input([1,3,2,2,2])

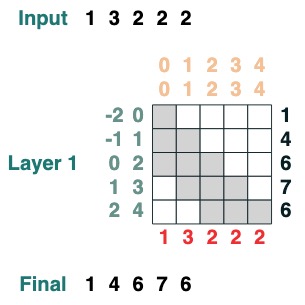
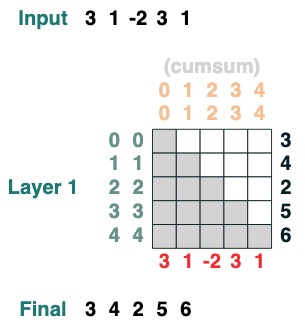
Hier ist ein Beispiel, das die kumulative Summe berechnen kann Hier führen wir die Möglichkeit ein, die Transformation zu benennen, um Ihnen beim Debuggen zu helfen.

def cumsum(seq=tokens):
    x = (before | (key(indices) == query(indices))).value(seq)
    return x.name("cumsum")
cumsum().input([3, 1, -2, 3, 1])

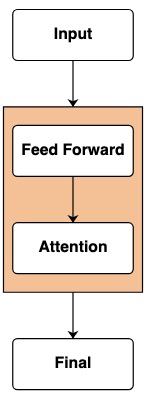
Schicht

Die Sprache unterstützt das Kompilieren komplexerer Transformationen. Es berechnet auch Schichten, indem es jede Operation verfolgt.

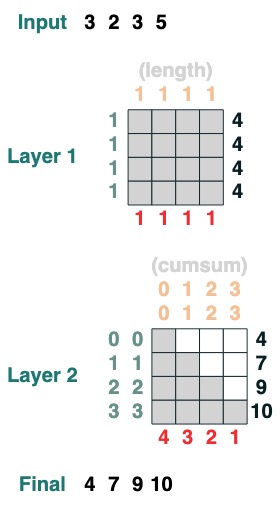
Hier ist ein Beispiel für eine zweischichtige Transformation, wobei die erste der Berechnung der Länge und die zweite der kumulativen Summe entspricht.

x = cumsum(length - indices)
x.input([3, 2, 3, 5])

Programmieren mit Transformatoren

Mit dieser Bibliothek können wir eine komplexe Aufgabe schreiben. Gail Weiss stellte mir eine äußerst herausfordernde Frage, um diesen Schritt aufzuschlüsseln: Können wir einen Transformer laden, der Zahlen beliebiger Länge hinzufügt?

Beispiel: Können wir bei einer Zeichenfolge „19492+23919“ die richtige Ausgabe laden?

Wenn Sie es selbst ausprobieren möchten, stellen wir Ihnen eine Version Sie selbst ausprobieren können.

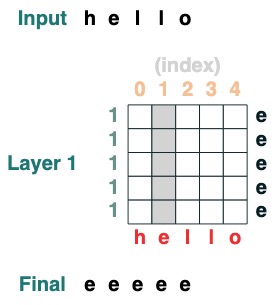
Herausforderung 1: Wähle einen gegebenen Index

lädt eine Sequenz mit allen Elementen iam

def index(i, seq=tokens):
    x = (key(indices) == query(i)).value(seq)
    return x.name("index")
index(1)

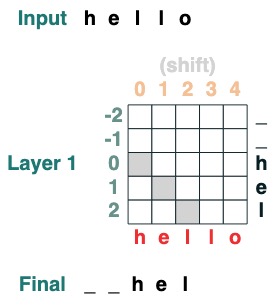
Herausforderung Zwei: Bekehrung

iBewege alle Spielsteine ​​um die Position nach rechts .

def shift(i=1, default="_", seq=tokens):
    x = (key(indices) == query(indices-i)).value(seq, default)
    return x.name("shift")
shift(2)

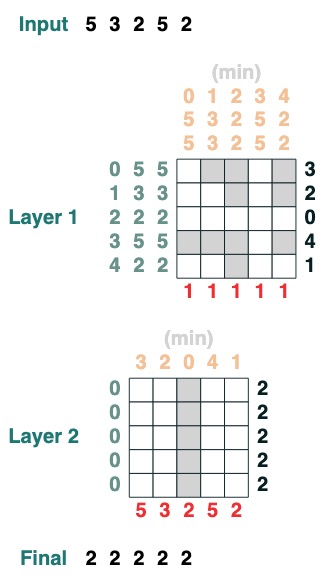
Herausforderung drei: Minimieren

Berechnet den Minimalwert einer Folge. (Dieser Schritt wird schwierig, unsere Version verwendet einen 2-Schichten-Aufmerksamkeitsmechanismus)

def minimum(seq=tokens):
    sel1 = before & (key(seq) == query(seq))
    sel2 = key(seq) < query(seq)
    less = (sel1 | sel2).value(1)
    x = (key(less) == query(0)).value(seq)
    return x.name("min")
minimum()([5,3,2,5,2])

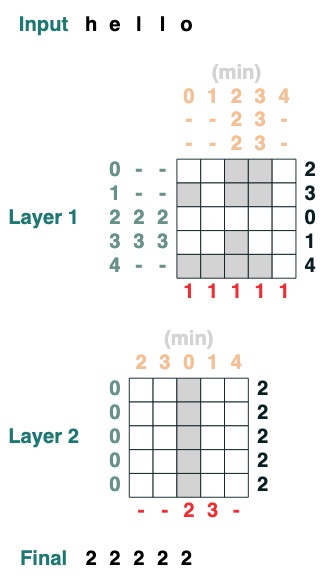
Herausforderung vier: Erster Index

Berechnen Sie den ersten Index mit Token q (2 Schichten)

def first(q, seq=tokens):
    return minimum(where(seq == q, indices, 99))
first("l")

Herausforderung fünf: Rechte Ausrichtung

Richtet eine Auffüllsequenz rechtsbündig aus. Beispiel: " ralign().inputs('xyz___') ='—xyz'" (2 Ebenen)

def ralign(default="-", sop=tokens):
    c = (key(sop) == query("_")).value(1)
    x = (key(indices + c) == query(indices)).value(sop, default)
    return x.name("ralign")
ralign()("xyz__")

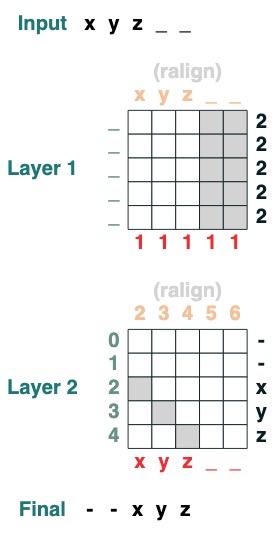
Herausforderung Sechs: Trennung

Teilen Sie eine Sequenz am Token "v" in zwei Teile und richten Sie sie rechts aus (2 Ebenen):

def split(v, i, sop=tokens):

    mid = (key(sop) == query(v)).value(indices)
    if i == 0:
        x = ralign("0", where(indices < mid, sop, "_"))
        return x
    else:
        x = where(indices > mid, sop, "0")
        return x
split("+", 1)("xyz+zyr")


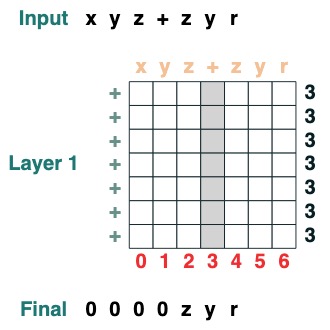
split("+", 0)("xyz+zyr")

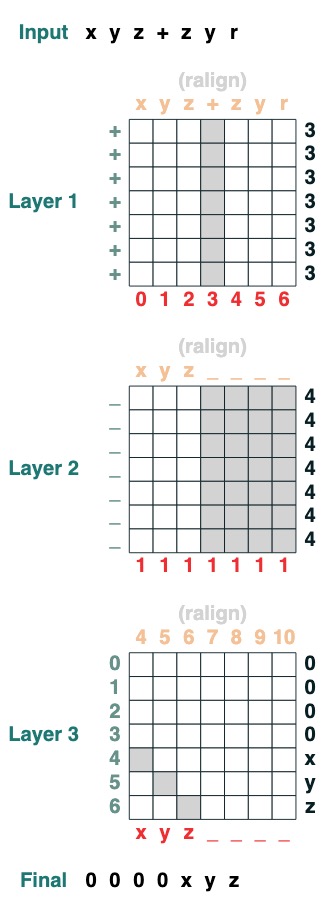
Herausforderung Sieben: Streichen

Ersetzen Sie das spezielle Token „<“ durch den nächsten „<“-Wert (2 Ebenen):

def slide(match, seq=tokens):
    x = cumsum(match) 
    y = ((key(x) == query(x + 1)) & (key(match) == query(True))).value(seq)
    seq =  where(match, seq, y)
    return seq.name("slide")
slide(tokens != "<").input("xxxh<<<l")

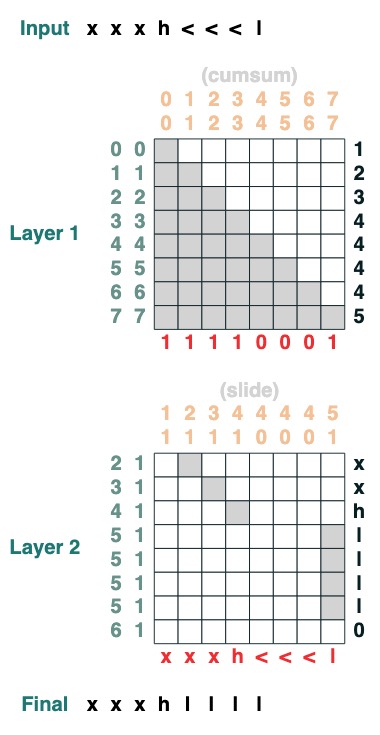
Herausforderung Acht: Erhöhen

Sie möchten die Addition zweier Zahlen durchführen. Hier sind die Schritte.

add().input("683+345")
  1. In zwei Teile teilen. Auf Plastik umstellen. dazu kommen

„683+345“ => [0, 0, 0, 9, 12, 8]

  1. Berechnen Sie die Übertragsklausel. Drei Möglichkeiten: 1 trägt, 0 trägt nicht, < vielleicht trägt.

[0, 0, 0, 9, 12, 8] => „00<100“

  1. Gleitender Übertragskoeffizient

„00<100“ => 001100“

  1. komplette Ergänzung

Dies sind 1 Zeile Code. Das komplette System besteht aus 6 Aufmerksamkeitsmechanismen. (Obwohl Gail sagt, dass Sie es in 5 schaffen können, wenn Sie vorsichtig genug sind!).

def add(sop=tokens):
    # 0) Parse and add
    x = atoi(split("+", 0, sop)) + atoi(split("+", 1, sop))
    # 1) Check for carries 
    carry = shift(-1, "0", where(x > 9, "1", where(x == 9, "<", "0")))
    # 2) In parallel, slide carries to their column                                         
    carries = atoi(slide(carry != "<", carry))
    # 3) Add in carries.                                                                                  
    return (x + carries) % 10
add()("683+345")


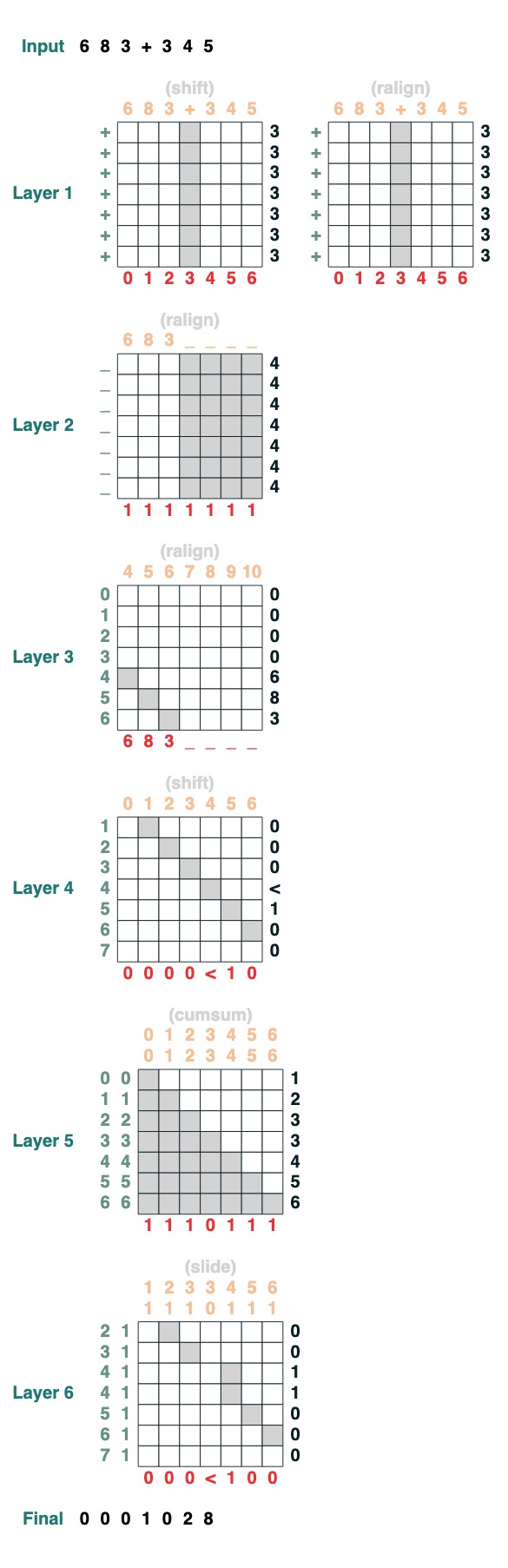
683 + 345

1028

Perfekt gemacht!

Referenzen & Links im Text:

<hr>

Englischer Originaltext: Thinking Like Transformers

Übersetzer: innovation64 (Li Yang)

{{o.name}}
{{m.name}}

Ich denke du magst

Origin my.oschina.net/HuggingFace/blog/7564937
Empfohlen
Rangfolge
Täglich
Mehr
2025-04-30(0)
2025-04-29(0)
2025-04-28(0)
2025-04-27(0)
2025-04-26(0)
2025-04-25(0)
2025-04-24(0)
2025-04-23(0)
2025-04-22(0)
2025-04-21(0)

Code World

© 2018 codetd.com