Zusammenfassung: Merge Sort und Quick Sort sind zwei etwas komplizierte Sortieralgorithmen. Beide verwenden die Idee von Divide and Conquer. Die Codes werden durch Rekursion implementiert, und der Prozess ist sehr ähnlich. Der Schlüssel zum Verständnis der Zusammenführungssortierung besteht darin, die Rekursionsformel und die Zusammenführungsfunktion merge() zu verstehen.
Dieser Artikel wurde von der Huawei Cloud Community „ Eight Sorting Algorithms in Simple Ways “, Autor: Embedded Vision, geteilt.
Merge Sort und Quick Sort sind zwei etwas komplizierte Sortieralgorithmen. Beide verwenden die Idee von Divide and Conquer, und der Code wird durch Rekursion implementiert. Der Prozess ist sehr ähnlich. Der Schlüssel zum Verständnis der Zusammenführungssortierung besteht darin, die Rekursionsformel und die Zusammenführungsfunktion merge() zu verstehen.
Eins, Blasensortierung (Bubble Sort)
Der Sortieralgorithmus ist eine Art Algorithmus, den Programmierer verstehen und mit dem sie vertraut sein müssen. Es gibt viele Arten von Sortieralgorithmen, wie zum Beispiel: Bubbling, Insertion, Selection, Fast, Merge, Counting, Cardinality und Bucket Sorting.
Bubble Sort arbeitet nur mit zwei benachbarten Daten. Bei jedem Blasenbildungsvorgang werden zwei benachbarte Elemente verglichen, um zu sehen, ob sie die Anforderungen an das Größenverhältnis erfüllen, und wenn nicht, werden sie ausgetauscht. Ein Sprudeln bewegt mindestens ein Element dorthin, wo es sein sollte, und wiederholt sich n-mal, um die Sortierung von n Daten abzuschließen.
Zusammenfassung: Wenn das Array n Elemente hat, sind im schlimmsten Fall n Bubbling-Operationen erforderlich.
Der C++-Code des grundlegenden Bubble-Sort-Algorithmus lautet wie folgt:
// 将数据从小到大排序
void bubbleSort(int array[], int n){
if (n<=1) return;
for(int i=0; i<n; i++){
for(int j=0; j<n-i; j++){
if (temp > a[j+1]){
temp = array[j]
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
}Tatsächlich kann der obige Bubble-Sorting-Algorithmus auch optimiert werden.Wenn eine bestimmte Bubbling-Operation keinen Datenaustausch mehr durchführt, bedeutetdas, dass das Array bereits in Ordnung ist und es nicht notwendig ist, nachfolgendeBubbling-Operationen durchzuführen. Der optimierte Code lautet wie folgt:
// 将数据从小到大排序
void bubbleSort(int array[], int n){
if (n<=1) return;
for(int i=0; i<n; i++){
// 提前退出冒泡循环发标志位
bool flag = False;
for(int j=0; j<n-i; j++){
if (temp > a[j+1]){
temp = array[j]
a[j] = a[j+1];
a[j+1] = temp;
flag = True; // 表示本次冒泡操作存在数据交换
}
}
if(!flag) break; // 没有数据交换,提交退出
}
}Funktionen von Bubble Sort :
- Der Blasenbildungsprozess beinhaltet nur den Austausch benachbarter Elemente und erfordert nur ein konstantes Maß an temporärem Speicherplatz, sodass die Speicherplatzkomplexität O (1) O (1) ist, was ein In-Place-Sortieralgorithmus ist .
- Wenn es zwei benachbarte Elemente der gleichen Größe gibt, tauschen wir nicht aus, und die Daten der gleichen Größe ändern die Reihenfolge vor und nach dem Sortieren nicht, es handelt sich also um einen stabilen Sortieralgorithmus .
- Der ungünstigste Fall und die durchschnittliche Zeitkomplexität sind beide O(n2) O ( n 2 ), und die beste Zeitkomplexität ist O(n) O ( n ).
Zweitens, Insertion Sort (Insertion Sort)
- Der Insertion-Sort-Algorithmus unterteilt die Daten im Array in zwei Intervalle: das sortierte Intervall und das unsortierte Intervall. Der anfängliche sortierte Bereich hat nur ein Element, nämlich das erste Element des Arrays.
- Die Kernidee des Insertion-Sort-Algorithmus besteht darin, ein Element des unsortierten Bereichs zu nehmen, eine geeignete Position zum Einfügen in den sortierten Bereich zu finden und sicherzustellen, dass die Daten im sortierten Bereich immer in Ordnung sind.
- Wiederholen Sie diesen Vorgang, bis die unsortierten Intervallelemente leer sind, dann endet der Algorithmus.
Insertion Sort umfasst wie Bubble Sort auch zwei Operationen, eine ist der Vergleich von Elementen und die andere die Bewegung von Elementen .
Wenn wir ein Datenelement a in den sortierten Bereich einfügen müssen, müssen wir die Größe von a mit den Elementen des sortierten Bereichs vergleichen, um eine geeignete Einfügeposition zu finden. Nachdem wir den Einfügepunkt gefunden haben, müssen wir auch die Reihenfolge der Elemente nach dem Einfügepunkt um ein Bit nach hinten verschieben, um Platz für das einzufügende Element a zu schaffen.
Die C++-Codeimplementierung von Insertion Sort lautet wie folgt:
void InsertSort(int a[], int n){
if (n <= 1) return;
for (int i = 1; i < n; i++) // 未排序区间范围
{
key = a[i]; // 待排序第一个元素
int j = i - 1; // 已排序区间末尾元素
// 从尾到头查找插入点方法
while(key < a[j] && j >= 0){ // 元素比较
a[j+1] = a[j]; // 数据向后移动一位
j--;
}
a[j+1] = key; // 插入数据
}
}Funktionen zum Sortieren von Einfügungen:
- Insertion Sorting benötigt keinen zusätzlichen Speicherplatz, und die Platzkomplexität beträgt O(1) O (1), sodass Insertion Sorting auch ein In-Place-Sortieralgorithmus ist.
- Bei der Einfügungssortierung können wir für Elemente mit demselben Wert auswählen, dass die Elemente, die später erscheinen, hinter den Elementen eingefügt werden, die zuvor erschienen sind, sodass die ursprüngliche vordere und hintere Reihenfolge unverändert beibehalten werden kann, sodass die Einfügungssortierung stabil ist Sortieralgorithmus.
- Der ungünstigste Fall und die durchschnittliche Zeitkomplexität sind beide O(n2) O ( n 2 ), und die beste Zeitkomplexität ist O(n) O ( n ).
Drei, Auswahlsortierung (Selection Sort)
Die Implementierungsidee des Auswahlsortieralgorithmus ähnelt in gewisser Weise der Einfügungssortierung und wird ebenfalls in sortierte Intervalle und unsortierte Intervalle unterteilt. Aber die Auswahlsortierung findet jedes Mal das kleinste Element aus dem unsortierten Intervall und setzt es an das Ende des sortierten Intervalls.
Die Zeitkomplexität des besten Falls, des schlechtesten Falls und des durchschnittlichen Falls der Auswahlsortierung ist O(n2) O ( n 2), was ein direkter Sortieralgorithmus und ein instabiler Sortieralgorithmus ist .
Der C++-Code für die Auswahlsortierung wird wie folgt implementiert:
void SelectSort(int a[], int n){
for(int i=0; i<n; i++){
int minIndex = i;
for(int j = i;j<n;j++){
if (a[j] < a[minIndex]) minIndex = j;
}
if (minIndex != i){
temp = a[i];
a[i] = a[minIndex];
a[minIndex] = temp;
}
}
}Sortierzusammenfassung der Blaseneinfügungsauswahl
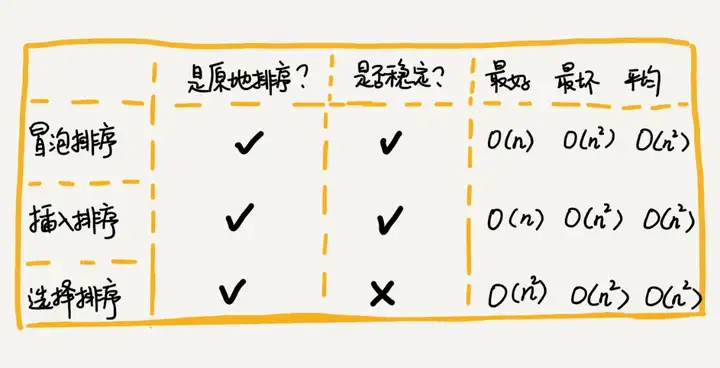
Die Implementierungscodes dieser drei Sortieralgorithmen sind sehr einfach und sie sind sehr effizient zum Sortieren kleiner Datenmengen. Beim Sortieren umfangreicher Daten ist die Zeitkomplexität jedoch immer noch etwas hoch, sodass eher ein Sortieralgorithmus mit einer Zeitkomplexität von O(nlogn) O ( nlogn ) verwendet wird.
Bestimmte Algorithmen hängen von bestimmten Datenstrukturen ab. Die obigen drei Sortieralgorithmen werden alle basierend auf Arrays implementiert.
Viertens: Sortieren zusammenführen (Merge Sort)
Die Kernidee von Merge Sort ist relativ einfach. Wenn wir ein Array sortieren wollen, teilen wir das Array zuerst von der Mitte aus in Vorder- und Hinterteil, sortieren dann Vorder- und Hinterteil separat und führen dann die sortierten beiden Teile zusammen , sodass das gesamte Array in Ordnung ist.
Merge Sort nutzt die Idee von Divide and Conquer. Teile und herrsche, wie der Name schon sagt, ist zu teilen und zu erobern, ein großes Problem in kleine Teilprobleme zu zerlegen, die es zu lösen gilt. Wenn die kleinen Teilprobleme gelöst sind, ist auch das große Problem gelöst.
Die „Teile-und-Herrsche“-Idee ist der rekursiven Idee etwas ähnlich, und der „Teile-und-Herrsche“-Algorithmus wird im Allgemeinen mit Rekursion implementiert. Teile und herrsche ist eine Verarbeitungsidee zum Lösen von Problemen, und Rekursion ist eine Programmiertechnik, und die beiden widersprechen sich nicht.
Da das Merge-Sorting das Teile-und-Herrsche-Denken verwendet und das Teile-und-Herrsche-Denken im Allgemeinen mithilfe von Rekursion implementiert wird, liegt der nächste Schwerpunkt auf der Verwendung von Rekursion zum Implementieren von Merge-Sortieren . Die Kunst beim Schreiben von rekursivem Code besteht darin, das Problem zu analysieren, um die rekursive Formel zu erhalten, dann die Beendigungsbedingung zu finden und schließlich die rekursive Formel in rekursiven Code zu übersetzen. Wenn Sie also den Code für Mergesort schreiben möchten, müssen Sie zuerst die rekursive Formel für Mergesort schreiben .
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解,即区间数组元素为 1 Der Pseudocode für Mergesort lautet wie folgt:
merge_sort(A, n){
merge_sort_c(A, 0, n-1)
}
merge_sort_c(A, p, r){
// 递归终止条件
if (p>=r) then return
// 取 p、r 中间的位置为 q
q = (p+r)/2
// 分治递归
merge_sort_c(A[p, q], p, q)
merge_sort_c(A[q+1, r], q+1, r)
// 将A[p...q]和A[q+1...r]合并为A[p...r]
merge(A[p...r], A[p...q], A[q+1...r])
}4.1, Analyse der Sortierleistung beim Zusammenführen
1. Mergesort ist ein stabiler Sortieralgorithmus . Analyse: Die Funktion merge_sort_c() im Pseudo-Code zerlegt nur das Problem und beinhaltet kein Verschieben von Elementen und Vergleichen von Größen. Der eigentliche Elementvergleich und die Datenverschiebung befinden sich im Teil der Funktion merge(). Beim Zusammenführen bleibt die Reihenfolge von Elementen mit gleichem Wert vor und nach dem Zusammenführen garantiert unverändert Merge-Sort-Sortieren ist ein stabiler Sortieralgorithmus.
2. Die Ausführungseffizienz von Mergesort hat nichts mit dem Ordnungsgrad des zu sortierenden ursprünglichen Arrays zu tun, daher ist seine Zeitkomplexität sehr stabil, egal ob es sich um den besten Fall, den schlimmsten Fall oder den durchschnittlichen Fall handelt Zeitkomplexität ist O ( nlogn) O ( nlogn ). Analyse: Nicht nur das rekursive Lösungsproblem kann als rekursive Formel geschrieben werden, sondern auch die Zeitkomplexität des rekursiven Codes kann als rekursive Formel geschrieben werden:

3. Die Raumkomplexität ist O(n) . Analyse: Die Raumkomplexität von rekursivem Code summiert sich nicht wie die Zeitkomplexität. Obwohl jede Zusammenführungsoperation des Algorithmus zusätzlichen Speicherplatz beantragen muss, wird der vorübergehend geöffnete Speicherplatz freigegeben, nachdem die Zusammenführung abgeschlossen ist. Zu jedem Zeitpunkt wird die CPU nur eine Funktion ausführen und daher nur einen temporären Speicherplatz verwenden. Der maximale temporäre Speicherplatz wird die Größe von n Daten nicht überschreiten, daher ist die Platzkomplexität O(n) O ( n ).
Fünf, schnelle Sortierung (Quicksort)
Die Idee von Quicksort ist folgende: Wenn wir einen Datensatz mit Indizes von p bis r im Array sortieren wollen, wählen wir beliebige Daten zwischen p und r als Drehpunkt (Partitionspunkt ) . Wir durchlaufen die Daten zwischen p und r, platzieren die Daten kleiner als der Pivot auf der linken Seite, platzieren die Daten größer als der Pivot auf der rechten Seite und platzieren den Pivot in der Mitte. Nach diesem Schritt werden die Daten zwischen dem Array p und r in drei Teile geteilt: Die Daten zwischen p und q-1 vorne sind kleiner als der Pivot, die Mitte ist der Pivot und die Daten zwischen q+1 und r größer als der Pivot ist.
Gemäß der Idee von Teile und Herrsche und Rekursion können wir die Daten mit Indizes von p bis q-1 und die Daten mit Indizes von q+1 bis r rekursiv sortieren, bis das Intervall auf 1 reduziert ist, was bedeutet, dass alle Die Daten sind alle in Ordnung.
Die Rekursionsformel lautet wie folgt:
递推公式:
quick_sort(p,r) = quick_sort(p, q-1) + quick_sort(q, r)
终止条件:
p >= rSortierung und Zusammenfassung der schnellen Sortierung zusammenführen
Merge Sort und Quick Sort sind zwei etwas komplizierte Sortieralgorithmen. Beide verwenden die Idee von Divide and Conquer, und der Code wird durch Rekursion implementiert. Der Prozess ist sehr ähnlich. Der Schlüssel zum Verständnis der Zusammenführungssortierung besteht darin, die Rekursionsformel und die Zusammenführungsfunktion merge() zu verstehen. Ebenso ist der Schlüssel zum Verständnis von Quicksort das Verständnis der rekursiven Formel sowie der Partitionsfunktion partition().
Zusätzlich zu den obigen 5 Sortieralgorithmen gibt es 3 lineare Sortieralgorithmen , deren Zeitkomplexität O(n) O ( n ) ist: Bucket-Sortierung, Zählsortierung und Radix-Sortierung. Die Leistung dieser acht Sortieralgorithmen ist in der folgenden Abbildung zusammengefasst:
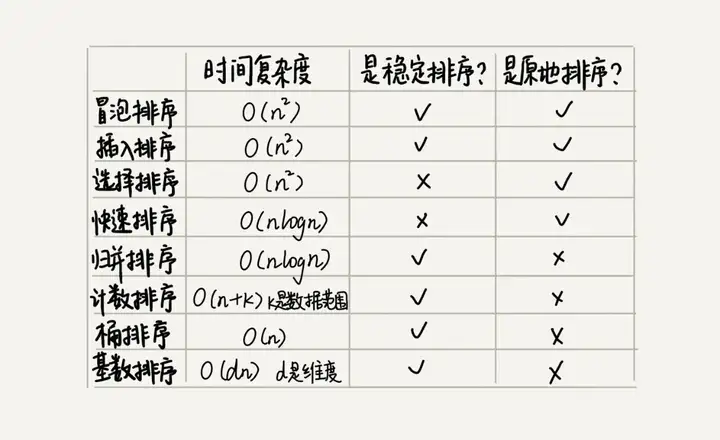
Verweise
- Sortieren (Teil 1): Warum ist Insertion Sort beliebter als Bubble Sort?
- Sortieren (unten): Wie findet man das K-te größte Element in O(n) mit der Idee der schnellen Sortierung?