Zusammenfassung: Backpropagation bezieht sich auf die Methode zur Berechnung des Gradienten der Parameter eines neuronalen Netzes.
Dieser Artikel wird von der Huawei Cloud Community „ Detailed Explanation of Backpropagation and Gradient Descent “, Autor: Embedded Vision, geteilt.
1. Vorwärtsausbreitung und Rückwärtsausbreitung
1.1, neuronaler Netzwerk-Trainingsprozess
Der Trainingsprozess für neuronale Netze ist:
- „Erraten“ Sie zuerst ein Ergebnis (Vorwärtsausbreitungsprozess des Modells) durch Zufallsparameter, das hier als Vorhersageergebnis a bezeichnet wird ;
- Berechnen Sie dann die Lücke zwischen a und dem Musterlabelwert y (d. h. den Berechnungsprozess der Verlustfunktion);
- Aktualisieren Sie dann die Neuronenparameter durch den Backpropagation-Algorithmus und versuchen Sie es erneut mit den neuen Parametern. Diesmal ist es keine "Vermutung", sondern die Annäherung an die richtige Richtung mit einer Basis. Schließlich ist die Anpassung der Parameter strategisch (basierend auf die Gradient-Drop-Strategie).
Die obigen Schritte werden viele Male wiederholt, bis es fast keinen Unterschied zwischen dem vorhergesagten Ergebnis und dem tatsächlichen Ergebnis gibt, das heißt |a – y|→0, dann endet das Training.
1.2, Vorwärtsausbreitung
Vorwärtsausbreitung (oder Vorwärtsdurchlauf) bezieht sich auf: Berechnen und Speichern der Ergebnisse jeder Schicht im neuronalen Netzwerk in der Reihenfolge (von der Eingabeschicht zur Ausgabeschicht).
Um den Berechnungsprozess der Vorwärtsausbreitung besser zu verstehen, können wir das Vorwärtsausbreitungsberechnungsdiagramm des Netzwerks gemäß der Netzwerkstruktur zeichnen. Die folgende Abbildung ist ein Beispiel für ein einfaches Netzwerk und den entsprechenden Berechnungsgraphen:
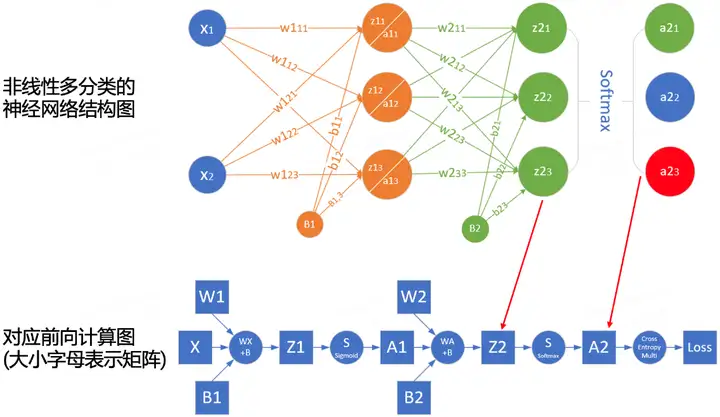
Die Quadrate stellen Variablen dar, und die Kreise stellen Operatoren dar. Die Richtung des Datenflusses wird sequentiell von links nach rechts berechnet.
1.3, Backpropagation
Backpropagation (Rückwärtsausbreitung, als BP bezeichnet) bezieht sich auf das Verfahren zur Berechnung des Gradienten von neuronalen Netzwerkparametern . Sein Prinzip basiert auf der Kettenregel im Kalkül , durchläuft das Netzwerk von der Ausgabeschicht zur Eingabeschicht in umgekehrter Reihenfolge und berechnet der Reihe nach den Gradienten jeder Zwischenvariablen und jedes Parameters.
Die automatische Berechnung von Gradienten (Automatic Differentiation) vereinfacht die Implementierung von Deep-Learning-Algorithmen erheblich.
Beachten Sie, dass der Backpropagation-Algorithmus die in der Vorwärtspropagation gespeicherten Zwischenwerte wiederverwendet, um wiederholte Berechnungen zu vermeiden. Daher müssen die Zwischenergebnisse der Vorwärtspropagation erhalten bleiben, was auch dazu führt, dass das Modelltraining mehr Speicher benötigt als die reine Vorhersage (Videospeicher). Gleichzeitig ist die von diesen Zwischenergebnissen belegte Speichergröße (Videospeicher) proportional zur Anzahl der Netzwerkschichten und zur Stapelgröße (batch_size), sodass die Verwendung einer großen Stapelgröße zum Trainieren eines tieferen Netzwerks eher zu einem Out of führen wird Speicherfehler (nicht genügend Speicher)!
1.4, Zusammenfassung
- Die Vorwärtsausbreitung berechnet und speichert Zwischenvariablen sequentiell in dem Rechengraphen, der durch das neuronale Netzwerk definiert ist, von der Eingabeschicht bis zur Ausgabeschicht.
- Backpropagation berechnet und speichert die Gradienten der Zwischenvariablen und Parameter des neuronalen Netzes in umgekehrter Reihenfolge (von der Ausgangsschicht zur Eingangsschicht).
- Beim Training eines neuronalen Netzes verwenden wir nach der Initialisierung der Modellparameter abwechselnd Vorwärtsausbreitung und Backpropagation, basierend auf dem durch Backpropagation berechneten Gradienten, kombiniert mit dem stochastischen Gradientenabstiegsoptimierungsalgorithmus (oder anderen Optimierungsalgorithmen wie Adam), um die Modellparameter zu aktualisieren .
- Das Training von Deep-Learning-Modellen erfordert mehr Speicher als Vorhersagen.
Zweitens, Steigungsabstieg
2.1, Optimierung im Deep Learning
Die meisten Deep-Learning-Algorithmen beinhalten eine Form der Optimierung. Der Zweck des Optimierers besteht darin, die Netzwerkgewichtungsparameter so zu aktualisieren, dass wir den Minimalpunkt des Verlustwerts in der Verlustoberfläche glatt erreichen .
Es gibt viele Herausforderungen bei der Deep-Learning-Optimierung. Einige der ärgerlichsten sind lokale Minima, Sattelpunkte und verschwindende Gradienten.
- Lokales Minimum : Wenn für jede objektive Funktion f(x) der entsprechende Wert von f(x) bei x kleiner ist als der Wert von f(x) an jedem anderen Punkt in der Nähe von x Wenn der Wert von f(x) bei x das Minimum der Zielfunktion über den gesamten Bereich ist, dann ist f ( x ) ein globales Minimum.
- Sattelpunkt : Bezieht sich auf jede Position, an der alle Gradienten einer Funktion verschwinden, aber weder ein globales Minimum noch ein lokales Minimum ist.
- Verschwindender Gradient: Aus bestimmten Gründen ist der Gradient der Zielfunktion f nahe Null (d. h. das Problem des Verschwindens des Gradienten), was einer der Gründe ist, warum es ziemlich schwierig ist, das Deep-Learning-Modell vor der Einführung der ReLU-Aktivierung zu trainieren Funktion und ResNet.
Beim Deep Learning sind die meisten Zielfunktionen komplex und es gibt keine analytische Lösung, daher müssen wir numerische Optimierungsalgorithmen verwenden, und die Optimierungsalgorithmen in diesem Papier: SGD und Adam gehören zu dieser Kategorie.
2.2, wie man die Gradientenabstiegsmethode versteht
Der Gradientenabstiegsalgorithmus (GD) ist der gebräuchlichste Optimierer beim Training neuronaler Netzwerkmodelle. Obwohl der Gradientenabstieg beim Deep Learning selten direkt verwendet wird, ist sein Verständnis von grundlegender Bedeutung für das Verständnis von stochastischen Gradientenabstiegs- und stochastischen Mini-Batch-Gradientenabstiegsalgorithmen .
Die meisten Artikel verwenden das Beispiel „Eine Person ist auf einem Berg gefangen und muss schnell zum Grund des Tals hinabsteigen“, um die Gradientenabstiegsmethode zu verstehen, aber das ist nicht ganz richtig. In der Natur ist das beste Beispiel für einen Gradientenabstieg der Prozess des bergab fließenden Quellwassers:
- Wasser wird von der Schwerkraft beeinflusst und fließt an der aktuellen Position in die steilste Richtung , wobei es manchmal einen Wasserfall bildet ( die entgegengesetzte Richtung des Gefälles ist die Richtung, in der der Funktionswert am schnellsten abfällt );
- Der Weg des Wassers, das den Berg hinabfließt, ist nicht einzigartig, da es an derselben Stelle mehrere Stellen mit derselben Steilheit geben kann, was zu einer Umleitung führt (mehrere Lösungen sind möglich);
- Beim Auftreffen auf Schlaglöcher können sich Seen bilden und der Abwärtsvorgang wird beendet (die globale optimale Lösung kann nicht erhalten werden, aber eine lokale optimale Lösung).
Beispiele beziehen sich auf AI-EDU: Gradient Descent.
2.3, das Prinzip des Gradientenabstiegs
Die mathematische Formel für den Gradientenabstieg:
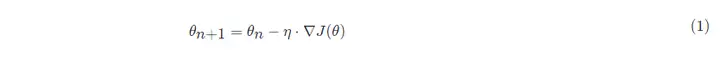
In:
- θn+1: der nächste Wert (aktualisierter Wert der Parameter im neuronalen Netz);
- θn: aktueller Wert (aktueller Parameterwert);
- −: Minuszeichen, die Umkehrung der Steigung (die Umkehrrichtung der Steigung ist die Richtung, in der der Funktionswert am schnellsten abfällt);
- η: Lernrate oder Schrittgröße, Kontrolle der von jedem Schritt zurückgelegten Distanz, nicht zu schnell, um die besten Aussichtspunkte nicht zu verpassen, nicht zu langsam, um zu lange Zeit zu vermeiden (Hyperparameter, die manuell angepasst werden müssen);
- ∇: Gradient, der am schnellsten ansteigende Punkt der aktuellen Position der Funktion (der Gradientenvektor zeigt bergauf, und der negative Gradientenvektor zeigt bergab);
- J(θ): Funktion (Zielfunktion, die darauf wartet, optimiert zu werden).
Die folgende Abbildung zeigt die Schritte der Gradientenabstiegsmethode. Der Zweck des Gradientenabstiegs besteht darin, den x- Wert an den Extrempunkt anzunähern.
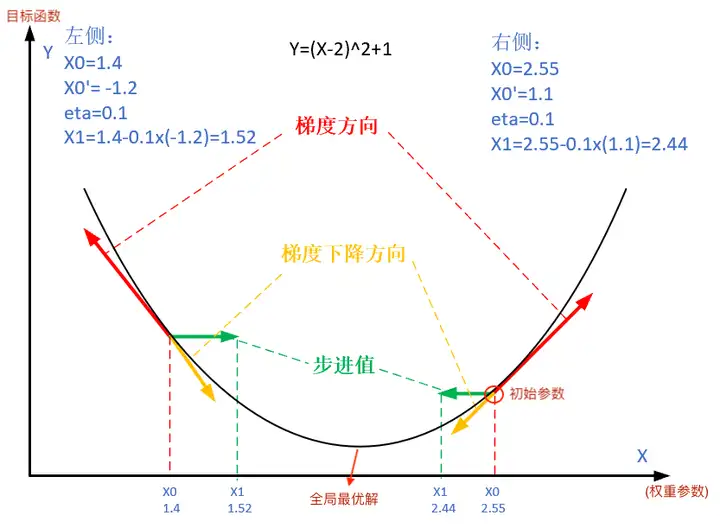

Da es bivariat ist, muss der iterative Prozess des Gradientenabstiegs mit einem dreidimensionalen Diagramm erklärt werden. Tabelle 2 visualisiert den Gradientenabstiegsprozess im 3D-Raum.
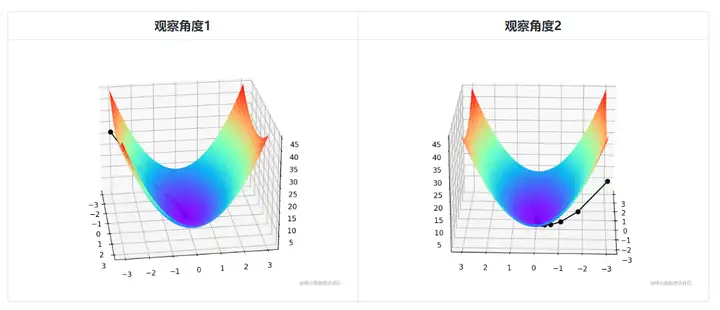
Die schwache schwarze Linie in der Mitte der Abbildung stellt den Prozess des Gradientenabstiegs dar, vom roten Hochland den ganzen Weg den Hang hinunter bis zur blauen Senke.
Der Prozess zur Gradientenabstiegsoptimierung und der Visualisierungscode der bivariaten konvexen Funktion J(x,y)=x2+2y2 lauten wie folgt:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def target_function(x,y):
J = pow(x, 2) + 2*pow(y, 2)
return J
def derivative_function(theta):
x = theta[0]
y = theta[1]
return np.array([2*x, 4*y])
def show_3d_surface(x, y, z):
fig = plt.figure()
ax = Axes3D(fig)
u = np.linspace(-3, 3, 100)
v = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(u, v)
R = np.zeros((len(u), len(v)))
for i in range(len(u)):
for j in range(len(v)):
R[i, j] = pow(X[i, j], 2)+ 4*pow(Y[i, j], 2)
ax.plot_surface(X, Y, R, cmap='rainbow')
plt.plot(x, y, z, c='black', linewidth=1.5, marker='o', linestyle='solid')
plt.show()
if __name__ == '__main__':
theta = np.array([-3, -3]) # 输入为双变量
eta = 0.1 # 学习率
error = 5e-3 # 迭代终止条件,目标函数值 < error
X = []
Y = []
Z = []
for i in range(50):
print(theta)
x = theta[0]
y = theta[1]
z = target_function(x,y)
X.append(x)
Y.append(y)
Z.append(z)
print("%d: x=%f, y=%f, z=%f" % (i,x,y,z))
d_theta = derivative_function(theta)
print(" ", d_theta)
theta = theta - eta * d_theta
if z < error:
break
show_3d_surface(X,Y,Z)Notiz! Zusammenfassend führen unterschiedliche Schrittweiten η zu unterschiedlichen Änderungen des Werts der optimierten Funktion J mit zunehmender Anzahl der Iterationen:
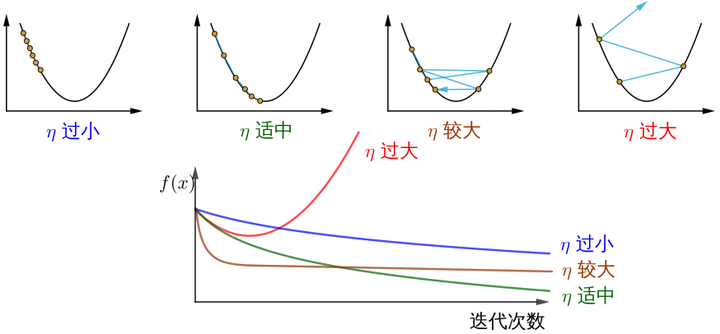
Wie versteht die Bildquelle die Gradientenabstiegsmethode? .
Drittens: stochastischer Gradientenabstieg und stochastischer Gradientenabstieg in kleinen Chargen
3.1, stochastischer Gradientenabstieg
Beim Deep Learning ist die Zielfunktion normalerweise der Durchschnitt der Verlustfunktion für jede Stichprobe im Trainingsdatensatz. Wenn ein Gradientenabstieg verwendet wird, beträgt der Rechenaufwand pro Iteration der unabhängigen Variablen O(n), der linear mit n (Anzahl der Abtastungen) wächst. Wenn der Trainingsdatensatz groß ist, ist der Rechenaufwand für den Gradientenabstieg pro Iteration daher hoch.
Stochastic Gradient Descent (SGD) reduziert den Rechenaufwand bei jeder Iteration. In jeder Iteration des stochastischen Gradientenabstiegs tasten wir eine zufällige Datenstichprobe gleichmäßig bei einem Index i ab, wobei i ∈ 1,...,n, und berechnen den Gradienten ∇J(θ), um den Gewichtungsparameter θ zu aktualisieren:

Der Rechenaufwand pro Iteration sinkt von O(n) für den Gradientenabstieg auf eine Konstante O(1). Außerdem muss betont werden, dass der stochastische Gradient ∇J(θ) eine unvoreingenommene Schätzung des vollen Gradienten ∇J(θ) ist.
Eine unverzerrte Schätzung ist eine unverzerrte Schlussfolgerung, wenn eine Stichprobenstatistik zum Schätzen eines Populationsparameters verwendet wird.
In praktischen Anwendungen muss das stochastische Gradientenabstiegs-SGD-Verfahren in Kombination mit dem dynamischen Lernratenverfahren verwendet werden , da ansonsten die Kombination aus fester Lernrate + SGD den Modellkonvergenzprozess komplizierter macht.
3.2, stochastischer Mini-Batch-Gradientenabstieg
Die oben erwähnten Methoden des Gradientenabstiegs (GD) und des stochastischen Gradientenabstiegs (SGD) sind zu extrem, da sie entweder den vollständigen Datensatz verwenden, um den Gradienten zu berechnen und die Parameter zu aktualisieren, oder nur jeweils ein Trainingsmuster verarbeiten, um die Parameter zu aktualisieren. In tatsächlichen Projekten wird ein Kompromiss zwischen den beiden eingegangen, nämlich Minibatch-Gradientenabstieg.Die Verwendung von Minibatch-Gradientenabstieg kann auch die Berechnungseffizienzverbessern.
Alle Stichprobendatenelemente im Mini-Batch werden zufällig aus dem Trainingssatz gezogen, und die Anzahl der Stichproben ist batch_size (abgekürzt als bs).
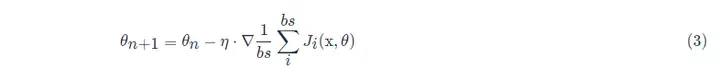
Darüber hinaus verwendet der SGD-Optimierungsalgorithmus, der in allgemeinen Projekten verwendet wird, standardmäßig einen stochastischen Gradientenabstieg mit kleinen Stapeln, d.
Verweise
- Wie ist die Gradientenabstiegsmethode zu verstehen?
- AI-EDU: Gradientenabstieg
- "Hands-on Deep Learning Kapitel 11 - Optimierungsalgorithmen"