Bitte geben Sie die Quelle für den Originalnachdruck von Yunzhi QMS an
Autor: Wang Hongshi
1. Was ist ein Streudiagramm?
Streudiagramm (Scatter Plot oder Scatter Chart), auch Punktdiagramm genannt, ist, wie der Name schon sagt, ein Diagramm, das aus einigen verstreuten Punkten besteht.Die Position dieser Punkte wird durch ihre X- und Y-Werte bestimmt. Daher wird es auch als XY-Streudiagramm bezeichnet. Es zeigt alle Daten in Form von Punkten auf dem kartesischen Koordinatensystem an, um den Grad der Wechselwirkung zwischen Variablen zu zeigen, und die Position des Punktes wird durch den Wert der Variablen bestimmt.
Bei der Analyse unabhängiger Daten können Sie das Histogramm und Plato verwenden, um den Verbesserungspunkt direkt zu finden, aber wenn Sie die Korrelation zwischen den beiden Variablen X und Y analysieren möchten, müssen Sie das Streudiagramm verwenden. Wie die Abschrecktemperatur und Härte von Stahl, das Drehmoment und die Zugfestigkeit von Schrauben, die Temperatur und Viskosität von Öl, der Bleigehalt und die Strahlungsbeständigkeit von Glas usw.
Streudiagramme werden häufig verwendet, um die Beziehung zwischen zwei kontinuierlichen Variablen X und Y auszudrücken. Jeder Punkt in der Abbildung stellt jede Stichprobe im Zieldatensatz dar. Die Verteilung der Datenpunkte auf der kartesischen Koordinatenebene und der abhängigen Variablen variiert mit dem Allgemeinen Trend der Variable. Aus diesem Trend kann die geeignete Funktion ausgewählt werden, um die empirische Verteilung anzupassen.Gleichzeitig werden einige Geraden und Kurven häufig in das Streudiagrammeingepasst, um bestimmte Modelle darzustellen, und dann die funktionale Beziehung zwischenVariablen finden.

2. Die Rolle des Streudiagramms
Ein Streudiagramm zeigt eine Reihe als eine Reihe von Punkten an, wobei Werte durch die Position der Punkte im Diagramm dargestellt werden und Kategorien durch eindeutige Markierungen im Diagramm dargestellt werden. Scatterplots werden oft verwendet, um aggregierte Daten über Kategorien hinweg zu vergleichen.Es gibt viele Anwendungen.Zwei gängige Anwendungen werden wie folgt zusammengefasst.
2.1 Regressionsanalyse
Das Streudiagramm wird in der Regressionsanalyse verwendet. Das Verteilungsdiagramm von Datenpunkten auf der Ebene des kartesischen Koordinatensystems. Das Streudiagramm zeigt den allgemeinen Trend der abhängigen Variablen an, die sich mit der unabhängigen Variablen ändern. Darauf basierend kann eine geeignete Funktion erstellt werden passend zu den Datenpunkten ausgewählt.
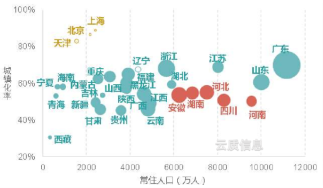
Nach der Regressionsanalyse kann das Streudiagramm verwandte Objekte vorhersagen und analysieren, sodass wir die verborgene Beziehung zwischen Variablen entdecken und dann wissenschaftliche Entscheidungen anstelle von Mehrdeutigkeiten treffen können. Das folgende Streudiagramm der Hauspreise kann uns zum Beispiel den Anstieg der Hauspreise in verschiedenen Städten intuitiv zeigen und eine wichtige Hilfestellung für spätere Anpassungen der Hauspreispolitik geben.

2.2 Korrelationsanalyse
Das Streudiagramm wird in der Korrelationsanalyse verwendet.Zwei Datensätze werden verwendet, um mehrere Koordinatenpunkte zu bilden, und dieVerteilung der Koordinatenpunkte wird untersucht, um festzustellen, ob eine bestimmteBeziehung zwischen den beiden Variablen besteht, oder um das Verteilungsmusterder zusammenzufassen Koordinatenpunkte.
Indem wir die Verteilung von Datenpunkten in einem Streudiagramm betrachten, können wir Korrelationen zwischen Variablen ableiten. Wenn zwischen den Variablen keine Korrelation besteht, stellt das Streudiagramm zufällig verteilte diskrete Punkte dar. Wenn eine bestimmte Korrelation besteht, sind die meisten Datenpunkte relativ dicht und in einem bestimmten Trend vorhanden.
Der Kernwert des Scatterplots liegt darin, die Beziehung zwischen Variablen zu entdecken.Verstehen Sie diese Beziehung nicht einfach als lineare Regressionsbeziehung. Es gibt viele Beziehungen zwischen Variablen, wie z. B. lineare Beziehung, exponentielle Beziehung, logarithmische Beziehung usw. Natürlich ist keine Beziehung auch eine wichtige Beziehung.

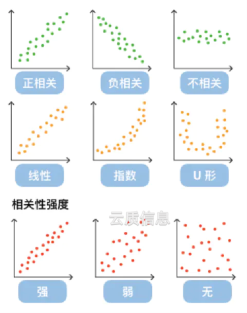
Die Korrelationsbeziehung von Daten wird hauptsächlich unterteilt in: positive Korrelation (zwei Variablenwerte steigen gleichzeitig), negative Korrelation (ein Variablenwert steigt und der andere Variablenwert sinkt), unkorreliert, lineare Korrelation, exponentielle Korrelation usw. , die im Streudiagramm angezeigt werden. Die ungefähre Verteilung ist in der folgenden Abbildung dargestellt. Die Punkte, die weit vom Punktcluster entfernt sind, werden als Ausreißer oder abnormale Punkte bezeichnet.
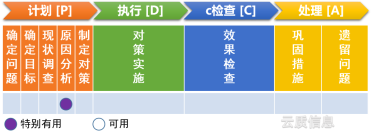
Aus der Sicht von PDCA lässt sich die Anwendung von Streudiagrammen wie folgt zusammenfassen:
3. Verformung des Streudiagramms
Basierend auf verschiedenen Anwendungsszenarien weist das Streudiagramm viele Verformungen auf, und einige häufige Verformungen sind unten aufgeführt.
- Scatterplot-Matrix
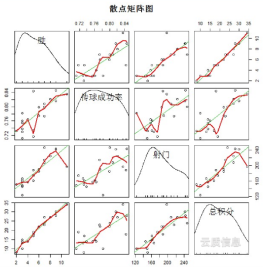
Wenn Sie die Korrelation zwischen mehreren Variablen gleichzeitig untersuchen möchten, ist es sehr mühsam, ein einfaches Streudiagramm zwischen ihnen einzeln zu zeichnen. Zu diesem Zeitpunkt kann die Scatterplot-Matrix verwendet werden, um die Scatterplots gleichzeitig unter den jeweiligen Variablen zu zeichnen, sodass die Hauptkorrelation zwischen mehreren Variablen schnell gefunden werden kann, was besonders wichtig ist, wenn eine multiple lineare Regression durchgeführt wird. Die Streudiagramm-Matrix unten zeigt die Beziehung zwischen Team-Punktesummen, Siegen, Passerfolgsquote und Torschüssen.
- 3D-Streudiagramm
Obwohl die Beziehung zwischen mehreren Variablen gleichzeitig in der Streudiagrammmatrix beobachtet werden kann, können einige wichtige Informationen übersehen werden, wenn die Zwei-mal-Zwei-Beobachtung des ebenen Streudiagramms durchgeführt wird. Das dreidimensionale Streudiagramm soll die Beziehung zwischen Variablen im dreidimensionalen Raum untersuchen, der durch die drei Variablen bestimmt wird Da die drei Variablen gleichzeitig betrachtet werden, können häufig Informationen gefunden werden, die in der zweidimensionalen Grafik nicht zu finden sind gefunden. Das dreidimensionale Streudiagramm unten zeigt die Beziehung zwischen der Gesamtpunktzahl, den Siegen und den Torschüssen des Teams.

- Blasendiagramm
Ein Blasendiagramm kann verwendet werden, um die Beziehung zwischen drei Variablen darzustellen. In Spalten auf einem Arbeitsblatt angeordnete Daten (x-Werte in der ersten Spalte, entsprechende y-Werte und Blasengrößenwerte in benachbarten Spalten) können in einem Blasendiagramm dargestellt werden.
Blasendiagramme ähneln Streudiagrammen, außer dass sie es ermöglichen, eine zusätzliche Größenvariable in das Diagramm aufzunehmen. In der Tat ist es so, als würde man einen Graphen mit drei Variablen in zwei Dimensionen zeichnen. Blasen werden durch Markierungen unterschiedlicher Größe dargestellt (die die relative Wichtigkeit angeben).
4. Anwendung des Streudiagramms
Die Anwendung von Streudiagrammen hat viele Vorteile, und die häufig verwendeten Punkte werden wie folgt zusammengefasst:
- Die Beziehung zwischen Ursache und Ergebnis kann gefunden werden: Sammeln Sie die Daten der Ursache und die Daten des Ergebnisses und vergleichen Sie sie.
- Zeichnen Sie ein Streudiagramm, um die Ergebnisse auf einen Blick zu sehen: Im Streudiagramm werden die Datenpunkte von Ursache und Wirkung durch X- und Y-Koordinaten dargestellt.
- Es kann beurteilt werden, ob eine Beziehung besteht oder nicht: Die Beziehung zwischen den beiden Datensätzen ist aus dem Streudiagramm klar ersichtlich.
Hinweis: Wenn die gesammelten Daten nicht anhand des Diagramms beurteilt werden können, sollten sie zuerst von der Ebene getrennt und dann angeklickt werden, um ein Streudiagramm zu zeichnen.
Die in der folgenden Tabelle aufgelisteten Daten sind die Aufzeichnungstabelle der Abschrecktemperatur X und der Härte Y eines bestimmten gesammelten Stahlstücks. Gibt es einen Zusammenhang zwischen den beiden Größen Abschrecktemperatur X und Härte Y?

Wenn Sie sich nur die Daten in der obigen Tabelle ansehen, können Sie erkennen, welche Merkmale die obigen Daten haben? Definitiv nicht, aber wir stellen es als Streudiagramm dar, und die Daten haben eindeutig einen bestimmten Trend.

Es wird offensichtlicher, wenn wir eine Trendlinie hinzufügen.
